МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ - Тема: Решение задач по теме: «Расстояние от точки до плоскости, от прямой до плоскости, расстояние между плоскостями, между скрещивающимися прямыми, между произвольными фигурами в пространстве»

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Тема:

Решение задач по теме: «Расстояние от точки до плоскости, от прямой до плоскости, расстояние между плоскостями, между скрещивающимися прямыми, между произвольными фигурами в пространстве»

Цель работы: 

- применить  умения и навыки применения изученных теоретических фактов в ходе решения задач

Оборудование:

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

4. Ручка.

Задание:

Вариант 1.

1. Из точек А и В, лежащих в двух перпендикулярных плоскостях, проведены перпендикуляры АС и BD  к линии пересечения плоскостей. Найдите длину отрезка АВ , если АС = 12 см, BD = 15 см, СD = 16 см.  

2. Точка М лежит в плоскости квадрата АВСD, длина стороны которого равна 2. Найдите расстояние от М до квадрата, если расстояния от М до прямых, содержащих перпендикулярные стороны, равны 3 и 5.

3. Дан куб АВСDABCD, длина ребра которого равна а; K – середина [CD]; F – центр грани CDDC. Найдите расстояния 1) а) |A; (CDD)| б) |A; (BBD)| в) |A; (BCD)| г) |A; (ABD)| д) |A; (CDB)|

4. Дано: ∆АВС - равносторонний, О - середина АВ, ОD ┴ АВС. АВ=6см, ОD=3см. Найдите расстояния от т. D до плоскости АВС, от С до АDВ, от А до DОС.

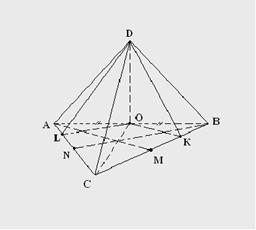
Вариант 2. 

1.Из точек М и К, лежащих в двух перпендикулярных плоскостях, проведены перпендикуляры  МС и KD к линии пересечения плоскостей. Найдите длину отрезка  CD, если  МС = 8 см, KD = 9 см, МК = 17 см.            

2.На плоскости лежит треугольник АВС, Может ли расстояние равняться расстоянию: а) г) расстоянию от Х до (АВ) и (АС)? б) в) расстоянию от Х до (АВ)

3. Дан куб АВСDABCD, длина ребра которого равна а; K – середина [CD]; F – центр грани CDDC. Найдите расстояния 1) а) |A; (CDD)| б) |A; (BBD)| в) |A; (BCD)| г) |A; (ABD)| д) |A; (CDB)|

4. Дано: ∆АВС - равносторонний, О - середина АВ, ОD ┴ АВС. АВ=6см, ОD=3см. Найдите расстояния от т. D до плоскости АВС, от С до АDВ, от А до DОС. . Найдите расстояния от точки D до прямых АВ, ВС, АС

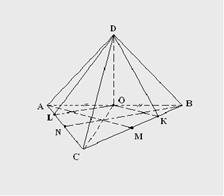
Порядок выполнения:

1.        Внимательно прочитать тему и цель практической работы.

2.        Изучить учебный материал по теме.

1.        Ответить на вопросы.

2.        Выполнить задания.

3.        Подготовить отчет.

Пояснения к работе (учебный материал):

Расстояния в пространстве

Расстояние от точки до прямой

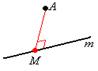
  Расстояние от точки до прямой – это длина перпендикуляра, проведенного из данной точки к данной прямой.                                                  

Между параллельными прямыми                                   От точки до плоскости             

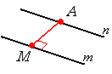
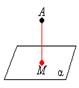
От прямой до плоскости                                           Между параллельными плоскостями                     

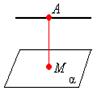
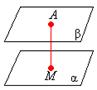
                                      Расстояние между скрещивающимися прямыми                                 

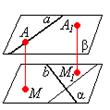
Определение: расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра

Определение. Общим перпендикуляром двух скрещивающихся прямых называется отрезок прямой, перпендикулярной обеим этим прямым, концы которого лежат на данных скрещивающихся прямых.

Теорема 3. Для любых двух скрещивающихся прямых существует общий перпендикуляр, и притом только один. Длина общего перпендикуляра не превосходит длины любого отрезка, концы которого принадлежат этим прямым.

Определение. Расстоянием между двумя скрещивающимися прямыми принимается равным длине их общего перпендикуляра.

Теорема 4. Расстояние между двумя скрещивающимися прямыми равно расстоянию от одной из этих прямых до плоскости, проходящей через другую из них параллельно первой.

Теорема 5. Расстояние между двумя скрещивающимися прямыми равно расстоянию между двумя параллельными плоскостями, проходящими через эти прямые.

Теорема 6. Расстояние между двумя скрещивающимися прямыми равно расстоянию между ортогональными проекциями этих прямых на плоскость перпендикулярную одной из этих прямых.

Вообще, расстоянием от точки  до фигуры Ф называется наименьшее из расстояний от этой точки до точек фигуры Ф. Иногда используют аналогичное определение расстояния между двумя непересекающимися фигурами; в частности, расстоянием между двумя параллельными или скрещивающимися прямыми.

При выполнении практической работы рассмотрите следующие примеры:

Пример 1:  

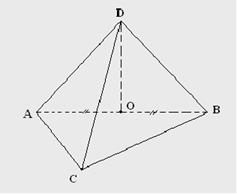
 1. Дано: ∆АВС - равносторонний, О - середина АВ, ОD ┴ АВС. АВ=6см, ОD=3см.

Найти пары перпендикулярных прямых.

Решение.

а) DO┴AB, DO┴AC, DOB (по определению прямой, перпендикулярной плоскости).

б) DC┴AB (по лемме, теореме о трех перпендикулярах).

2. Найти пары перпендикулярных прямой и плоскости.

Решение.

а) DO┴ABC(по условию).

б)AB┴COD, CO┴ADB (по признаку перпендикулярности прямой и плоскости).

3. Найти пары двух плоскостей.

Решение.

DAB┴ABC, DOC┴АВС, DOC┴ADB (по признаку перпендикулярности плоскостей).

Вопросы для закрепления теоретического материала к практическому занятию:

1.    Как определяется расстояние от точки до прямой на плоскости?

2.    Что принимают за расстояние между скрещивающимися прямыми?

3.    Сформулируйте теоремы о расстоянии между скрещивающимися прямыми.

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

1.    Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2.    Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

7.    Башмаков М.И. Математика: Учебник. — М., 2016.

Скачано с www.znanio.ru