
Публикация является частью публикации:
10.1 Piramida
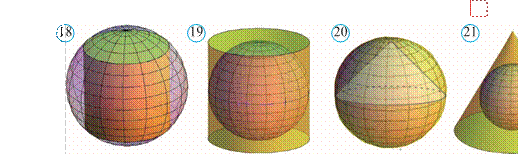
Bitta yog‘i ko‘pburchak, qolgan yoqlari esa umumiy uchga ega uchburchaklardan iborat ko‘pyoq piramida deb ataladi (1rasm).
Ko‘pburchak piramidaning asosi, uchburchaklar yon yoqlari, uchbur chaklarning tomonlari piramidaning qirralari, umumiy uсhi esa piramidaning uchi deb ataladi.
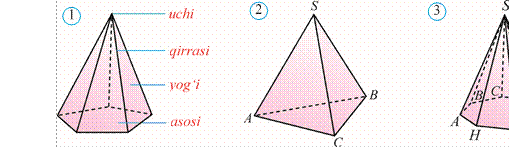
Asosining tomonlari soniga qarab piramidalar uchburchakli, to‘rtburchakli va hokazo nburchakli piramidalar deb yuritiladi. Uchburchakli piramida tetraedr deb ham ataladi (2rasm).
3 rasmda SABCDEFGH sakkizburchakli piramida tasvirlangan.
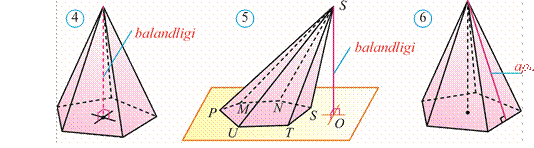
Piramida uchidan uning asos tekisligiga tushirilgan perpendikular uning balandligi deb ataladi (4 rasm).
Balandlik piramida asosiga tushmasligi ham mumkin (5rasm).
Bundan keyin asosi qavariq ko‘pburchakdan iborat piramidalarni qaraymiz. Bunday piramidalar qavariq bo‘ladi.
Piramida yon sirtining yuzi uning yon yoqlari yuzlarining yig‘indisidan iborat.
Piramida to‘la sirtining yuzi uning yon sirti va asosining yuzi yig‘indisiga teng: Sto‘la = Syon + Sasos.
Teorema. Agar piramida asosidagi barcha ikki yoqli burchaklari φ ga teng bo‘lsa, Sasos= Syon· cosφ bo‘ladi.
Bu ortogonal proyeksiya yuzi haqidagi teoremadan kelib chiqadi.
Muntazam piramida deb asosi muntazam ko‘pburchakdan iborat va balandligi asosining markaziga tushuvchi piramidaga aytiladi (6rasm).
Muntazam piramida yon yog‘ining piramida uchidan tushirilgan balandligi piramidaning apofemasi deb yuritiladi.
Muntazam piramidaning yon yoqlari, yon qirralari va apofemalari o‘zaro teng bo‘ladi. Shuningdek, uning asosidagi barcha ikki yoqli burchaklari, barcha yon qirralaridagi ikki yoqli burchaklari ham o‘zaro teng bo‘ladi.
Muntazam piramida balandligining ixtiyoriy nuqtasi piramida asosining uchlaridan va qirralaridan hamda yon yoqlaridan baravar uzoqlikda yotadi.
Agar piramidaning barcha yon qirralari o‘zaro teng bo‘lsa, u holda uning asosiga tashqi aylana chizish mumkin va bu aylana markazi piramida balandligi asosi bilan ustmaust tushadi (7rasm).
Agar piramida asosidagi barcha ikki yoqli burchaklari o‘zaro teng bo‘lsa, u holda uning asosiga ichki aylana chizish mumkin va bu aylana markazi piramida balandligi asosi bilan ustmaust tushadi (8rasm).
Teorema. Muntazam piramida yon sirtining yuzi
uning asosi yarim perimetri bilan apofemasining ko‘paytmasiga teng: Syon=![]() Pl, bu yerda P –
piramida asosining perimetri, l– apofemasi.
Pl, bu yerda P –
piramida asosining perimetri, l– apofemasi.
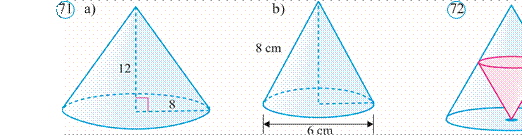
1-masala. Uchburchakli piramida asosining tomonlari 6, 8 va 10 ga teng. Piramidaning yon qirralari asosi tekisligi bilan bir xil burchak hosil qiladi. Agar piramidaning balandligi 4 ga teng bo‘lsa, uning yon qirrasi uzunligini toping.
Yechish: Piramida yon qirralari asosi tekisligi bilan bir xil burchak hosil qilgani uchun piramidaning balandligi uning asosiga tashqi chizilgan aylana markaziga tushadi (9rasm). Buni mustaqil asoslang.
Piramidaning asosi to‘g‘ri burchakli uchburchak bo‘ladi, chunki 6, 8, 10 – Pifagor sonlari: 62 + 82 = 102.
Ma’lumki, to‘g‘ri burchakli uchburchakka tashqi chizilgan aylana markazi gipotenuzaning o‘rtasida yotadi. Shunday qilib, piramidaning balandligi gipotenuzaning o‘rtasiga tushar ekan.
Piramidaning yon qirrasini – l, balandligini – H va asosining gipotenuzasini c bilan belgilaylik. Unda:
Pifagor teoremasiga ko‘ra l2 = H2 + ( c/2 )2 = 42 + 52 = 41.
![]()
![]() Demak, l = 41 . Javob: 41.
Demak, l = 41 . Javob: 41.
349. To‘rtburchakli muntazam piramidaning balandligi 12 cm, asosining tomoni 16 cm bo‘lsa, piramidaning yon qirrasini toping.
350. Uchburchakli muntazam piramidaning balandligi 1 cm, asosining tomoni 6 cm bo‘lsa, uning apofemasini toping.
351. Oltiburchakli muntazam piramidaning balandligi 8 cm, asosining tomoni 4 cm bo‘lsa, uning katta diagonal kesimining yuzini hisoblang.
352.
![]() To‘rtburchakli muntazam piramida
diagonal kesimining yuzi 12 2 cm2, piramidaning balandligi esa 4 cm. Piramida asosining
yuzini hisoblang.
To‘rtburchakli muntazam piramida
diagonal kesimining yuzi 12 2 cm2, piramidaning balandligi esa 4 cm. Piramida asosining
yuzini hisoblang.
353.
![]() Beshburchakli muntazam piramida
berilgan (10rasm). Piramida balandligi uning asosiga ichki chizilgan aylana
radiusiga teng. Asosining yuzi 800 ga
teng. Piramidaning yon sirtini toping.
Beshburchakli muntazam piramida
berilgan (10rasm). Piramida balandligi uning asosiga ichki chizilgan aylana
radiusiga teng. Asosining yuzi 800 ga
teng. Piramidaning yon sirtini toping.
354. Sakkizburchakli muntazam piramida berilgan (11rasm). Piramida yon
 ichki chizilgan aylana radiusini
toping. 11
ichki chizilgan aylana radiusini
toping. 11
355. DABC piramida yon yoqlarining D uchidan tushirilgan balandliklari 5 ga teng (12rasm). AB= 14, BC= 13, AC= 15. Piramida balandligini toping.
356. DABC piramida D uchidan tushirilgan yon yoqlarining balandliklari o‘zaro teng (13rasm). Piramida balandligi 4 ga teng. AB= 11, BC= 13, AC= 20. Piramidaning yon sirtini toping.
359. To‘rtburchakli muntazam piramida diagonal kesimining yuzi 40 cm2, piramidaning balandligi esa 5 cm. Piramida to‘la sirtining yuzini toping.
360. To‘rtburchakli muntazam piramida asosining tomoni 10 dm, apofemasi esa 6 cm ga teng bo‘lsa, uning yon sirtini toping.
361. Oltiburchakli muntazam piramida asosining tomonlari 12 dm, yon sirti 84 cm2 ga teng bo‘lsa, uning apofemasini toping.
362. Piramida asosidagi barcha ikki yoqli burchalari 60° ga, asosining yuzi 48 cm2 ga teng bo‘lsa, uning yon sirtini toping.
363. Piramida asosidagi barcha ikki yoqli burchalari 45° ga, yon sirti 48 cm2 ga teng bo‘lsa, uning asosi yuzini toping.
364*. Muntazam piramidaning a) yon yoqlari; b) yon qirralari; c) apofemalari o‘zaro teng bo‘lishini isbotlang.
365*. Muntazam piramidaning a) asosidagi barcha ikki yoqli burchaklari;
b) barc ha yon qirralaridagi ikki yoqli burchaklari o‘zaro teng bo‘lishini isbotlang.
366. Piramidaning asosi tomonlari 6 cm va 8 cm ga teng to‘g‘ri to‘rtburchakdan iborat. Piramidaning har bir qirrasi 13 cm ga teng bo‘lsa, uning balandligini toping.
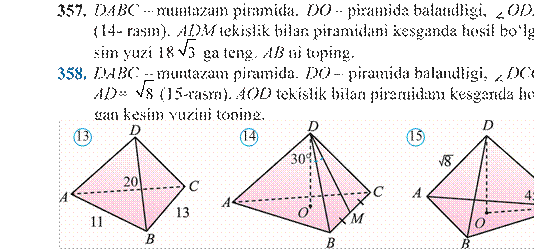
367. SABCD muntazam piramida berilgan (16rasm). Piramida balandligi 3 ga, yon sirtining yuzi esa 80 ga teng. Piramida to‘la sirtining yuzini toping.
368.
![]() SABCD
muntazam piramida berilgan (17rasm). Piramida yon sirtining yuzi 60 ga,
diagonal kesimining yuzi 12 2 ga teng. Piramida to‘la sirtining yuzini toping.
SABCD
muntazam piramida berilgan (17rasm). Piramida yon sirtining yuzi 60 ga,
diagonal kesimining yuzi 12 2 ga teng. Piramida to‘la sirtining yuzini toping.
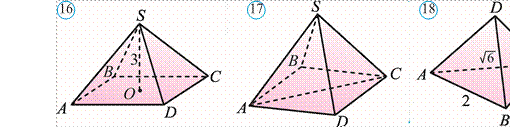
369. Tetraedrning barcha yon yoqlari asos tekisligi bilan 45° tashkil qiladi
![]() (18rasm). Asosining
tomonlari, mos ravishda, 2, 2 va 6 ga teng.
(18rasm). Asosining
tomonlari, mos ravishda, 2, 2 va 6 ga teng.
Tetraedr yon sirtining yuzini toping.
370. Tetraedrning barcha yon yoqlari asos tekisligi bilan 60° li burchak tashkil qiladi. Asosining tomonlari, mos ravishda, 7, 24 va 25 ga teng. Tetraedr yon sirtining yuzini toping.
371*. Piramidaning asosi – tomonlari 3 cm va 7 cm, diagonallaridan biri 6 cm ga teng bo‘lgan parallelogrammdan iborat. Piramidaning balandligi 4 cm ga teng bo‘lib, piramida diagonallarining kesishish nuqtasidan o‘tadi. Piramidaning yon qirrasini toping.
372*. Agar piramida asosidagi barcha ikki yoqli burchaklari φ ga, asosining
Sasos yuzi Sasos ga teng bo‘lsa, Syon= ![]() bo‘lishini isotlang. cosϕ
bo‘lishini isotlang. cosϕ
373*. Muntazam piramida balandligining ixtiyoriy nuqtasi piramida asosining uchlaridan va qirralaridan hamda yon yoqlaridan baravar uzoqlikda yotishini isbotlang.
374*. Agar piramidaning barcha yon qirralari o‘zaro teng bo‘lsa, u holda uning asosiga tashqi aylana chizish mumkinligini va bu aylana markazi piramida balandligi asosi bilan ustmaust tushishini isbotlang (7rasm).
375*. Agar piramida asosidagi barcha ikki yoqli burchaklari o‘zaro teng bo‘lsa, u holda uning asosiga ichki aylana chizish mumkinligini va bu aylana markazi piramida balandligi asosi bilan ustmaust tushishini isbotlang (8rasm).
10.2. Kesik piramida
Teorema. Piramidaning asosiga parallel va uni kesib o‘tadigan tekislik undan shu piramidaga o‘xshash piramida ajratadi.
Isbot. Aytaylik, S – piramidaning uchi, A – asosining uchi, A1 – kesuvchi tekislikning SA yon qirra bilan kesishish nuqtasi bo‘lsin (19 rasm).
![]() SA1
SA1
S nuqtaga nisbatan k = koeffitsiyentli gomotetiyani qaraymiz. Bu gomoSA
tetiyada ABC
uchburchak A1B1C1 uchburchakka
o‘tadi. Unda SABC piramida SA1B1C1 piramidaga o‘tadi. Mazkur gomotetiya o‘xshash
almashtirish bo‘lganligi uchun bu piramidalar o‘xshash bo‘ladi.![]()
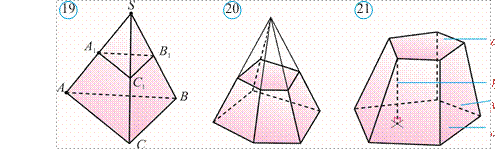
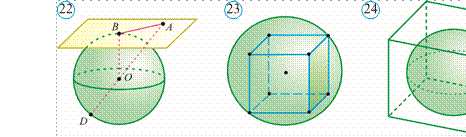
Piramidani uning asos tekisligiga parallel tekislik bilan kesamiz. Natijada u ikki bo‘lakka ajraladi (20rasm). Ulardan biri mazkur piramidaga o‘xshash bo‘lgan piramidadan, ikkinchisi esa kesik piramida deb ataluvchi ko‘pyoqdan iborat bo‘ladi. Kesik piramidaning parallel tekisliklarda yotgan yoqlari kesik piramidaning asoslari, qolgan yoqlari esa yon yoqlari deyiladi (21rasm). Kesik piramidaning asoslari o‘xshash ko‘pbur chaklardan, yon yoqlari esa trapetsiyalardan iborat.
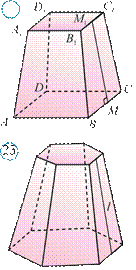 22 Kesik piramida balandligi uning ikki asoslari orasidagi
masofaga teng bo‘ladi. Kesik piramida muntazam piramidaning bo‘lagi bo‘lsa,
unga muntazam kesik piramida deyiladi.
22 rasmda ABCDA1B1C1D1 kesik piramida
tasvirlangan. ABCD va A1B1C1D1 parallel yoqlar uning asoslari, MM1 esa uning
apofemasidir.
22 Kesik piramida balandligi uning ikki asoslari orasidagi
masofaga teng bo‘ladi. Kesik piramida muntazam piramidaning bo‘lagi bo‘lsa,
unga muntazam kesik piramida deyiladi.
22 rasmda ABCDA1B1C1D1 kesik piramida
tasvirlangan. ABCD va A1B1C1D1 parallel yoqlar uning asoslari, MM1 esa uning
apofemasidir.
Teorema. Muntazam kesik piramida yon yog‘ining yuzi, asoslari perimetrlari yig‘indisining yarimi bilan apofemasi ko‘paytmasiga teng:
![]() Syon
Syon = ![]() (P1 + P l2) .
(P1 + P l2) .
Isbot. Muntazam nburchakli kesik piramida asoslarining perimetrlari va apofemasi, mos ravishda,
P1, P2 va l ga teng bo‘lsin (23rasm). Unda uning har
P1 va P2 ga hamda balandligi l ga teng bo‘lgan trapetsibir yog‘i tomonlari
n n
yadan iborat bo‘ladi.
Bunday trapetsiyalardan bittasining yuzi (P1 + P2 )⋅ ![]() l ga teng.
l ga teng.
n n 2
Unda berilgan kesik piramida yon sirtining yuzi
![]() P1 P2 l P1 + P2
P1 P2 l P1 + P2
Syon = n⋅( + )⋅ ![]() = ⋅l bo‘ladi. n n 2 2
= ⋅l bo‘ladi. n n 2 2
Oxirgi tenglikni boshqacha
Syon=![]() (a
+ b) nl
(a
+ b) nl
 ko‘rinishda ham
yozish mumkin, bu yerda a va b – kesik piramida asoslarining
tomoni.
ko‘rinishda ham
yozish mumkin, bu yerda a va b – kesik piramida asoslarining
tomoni.
Masala. Piramidaning yon qirrasi uchta teng qismga bo‘linib, uning bo‘linish nuqtalaridan asosiga parallel tekisliklar o‘tkazilgan (24rasm). Agar piramida asosining yuzi 360 cm2 ga teng bo‘lsa, uning kesimlari yuzini toping.
Yechish. Hosil bo‘lgan ikkita kesim piramida asosiga,
![]() 1 2 mos
ravishda, va o‘xshashlik koeffitsiyenti bilan o‘xshash bo‘ladi.
1 2 mos
ravishda, va o‘xshashlik koeffitsiyenti bilan o‘xshash bo‘ladi.
3 3
Ma’lumki, o‘xshash shakllar
yuzlarining nisbati ularning o‘xshashlik koeffitsiyenti kvadratiga teng. Unda
kesimlar yuzining piramida asosi yuziga nisbati, mos ravishda, ( )![]() va ( )
va ( )![]() bo‘ladi.
bo‘ladi.
Unda kesimlar yuzi: 360 ![]() =
40 (cm2) va
360
=
40 (cm2) va
360 ![]() = 160 (cm2) ga teng bo‘ladi. Javob:
40 cm2 va
160 cm2.
= 160 (cm2) ga teng bo‘ladi. Javob:
40 cm2 va
160 cm2. ![]()
 Yuqoridagi masaladan
kelib chiqib, piramida asosiga parallel tekislik bilan kesilganda unga o‘xshash
piramida hosil bo‘lishini hisobga olsak, quyidagi teoremani hosil qilamiz. Uni
mustaqil isbotlang.
Yuqoridagi masaladan
kelib chiqib, piramida asosiga parallel tekislik bilan kesilganda unga o‘xshash
piramida hosil bo‘lishini hisobga olsak, quyidagi teoremani hosil qilamiz. Uni
mustaqil isbotlang.
Teorema. Piramida asosiga parallel tekislik bilan kesilganda (25-rasm) hosil bo‘lgan piramida uchun
![]() a1 H1 S1 a1 2
a1 H1 S1 a1 2
= , = ( ) , bu yerda
a, H, S berilgan piramida, a H S a
a1, H1, S1 esa hosil bo‘lgan piramida asosining mos tomonlari, balandliklari va asoslarining yuzi.
Mavzuga oid masalalar va amaliy topshiriqlar
376. To‘rtburchakli muntazam kesik piramidaning asoslarining tomonlari 14 cm va 10 cm, diagonali esa 18 cm ga teng. Kesik piramidaning balandligini toping.
377. To‘rtburchakli muntazam kesik piramida asoslarining tomonlari 4 cm va 8 cm, diagonali esa 12 cm ga teng. Kesik piramidaning balandligini toping.
378. To‘rtburchakli muntazam kesik piramida asosining tomonlari 24 cm va 40 cm, balandligi esa 16 cm ga teng. Kesik piramidaning diagonalini toping.
379. To‘rtburchakli muntazam kesik piramida asoslarining tomonlari 12 cm va 36 cm, apofemasi 6 cm ga teng bo‘lsa, yon yog‘ining yuzini toping.
380. To‘rtburchakli muntazam kesik piramida asoslarining tomonlari 6 cm va 8 cm, yon yog‘i yuzi 84 cm2 ga teng bo‘lsa, uning apofemasini toping.
381. To‘rtburchakli muntazam kesik piramida asoslarining tomonlari 4 cm va 8 cm, diagonali 12 cm. Kesik piramidaning balandligini toping.
382. To‘rtburchakli muntazam kesik piramida asoslarining tomonlari 3 cm va 5 cm, diagonali 9 cm. Kesik piramidaning balandligini toping.
383. To‘rtburchakli muntazam kesik piramida asoslarining tomonlari 8 cm va 2 cm ga teng. Balandligi 4 ga teng. Uning to‘la sirtini toping.
384. To‘rtburchakli muntazam kesik piramida asoslarining diagonallari 6 va
![]() 10 ga,
balandligi 14
ga teng. Piramidaning apofemasini toping.
10 ga,
balandligi 14
ga teng. Piramidaning apofemasini toping.
385. Piramida uning asosiga parallel tekislik bilan kesilgan. Agar piramida asosining yuzi 40 cm2, hosil bo‘lgan kesim yuzi 10 cm2 va piramida balandligi 8 cm bo‘lsa, hosil bo‘lgan kesik piramida balandligini toping.
386. Piramida uning asosiga parallel tekislik bilan kesilgan. Agar piramida asosining yuzi 144 cm2, hosil bo‘lgan kesik piramida yuqori asosining yuzi 16 cm2 va balandligi 4 cm bo‘lsa, piramida balandligini toping.
387. Asosining yuzi Q1 ga teng bo‘lgan piramida berilgan. Uning asosiga parallel, undan h masofada yotgan va yuzi Q2 ga teng kesim o‘tkazilgan.
Piramidaning balandligini toping.
10.3. Piramidaning hajmi
Teorema. Uchburchakli piramidaning hajmi, asosining yuzi bilan balandligi ko‘paytmasining uchdan bir qismiga teng (26-rasm):
V = ![]() Sasos
Sasos ⋅ H.
Isbot. Aytaylik, OABC uchi O nuqtada, asosi ABC uchburchakdan iborat piramida bo‘lib, uning balandligi H ga va asosining yuzi S ga teng bo‘lsin.
Bu piramidani shunday asosga va shunday balandlikka ega bo‘lgan prizma bilan to‘ldiramiz (26rasm). Bu prizma uchta: berilgan piramida hamda yana ikkita OCC1B1 va OCBB1 piramidalardan tashkil topgan. OCC1B1 va OCBB1 piramidalarning balandliklari umumiy bo‘lib, asoslari CC1B1 va B1BC teng uchburchaklardan iborat. Shuning uchun ularning hajmlari ham teng bo‘ladi.
Xuddi shunga o‘xshash, OABC va OCBB1 piramidalarning C uchidan tushirilgan balandliklari umumiy bo‘lib, asoslari OAB va BB1O teng uchburchaklardan iborat. Shuning uchun ularning ham hajmlari teng bo‘ladi.
Demak, har uchala piramidalar hajmlari o‘zaro teng ekan. Ularning hajmlari yig‘indisi prizma hajmiga teng ekanligini hisobga olsak (27 rasm),
![]() 1
1
OABC
uchburchakli piramidaning hajmi V = ![]() Sasos ⋅
H
bo‘ladi.
Sasos ⋅
H
bo‘ladi.
3
Teorema. Ixtiyoriy piramidaning hajmi, asosining
yuzi bilan balandligi ko‘paytmasining uchdan biriga teng: V = ![]() Sasos
Sasos ⋅ H.
Bu teoremani 28 rasmdan foydalanib mustaqil isbotlang.
Mavzuga oid masalalar va amaliy topshiriqlar
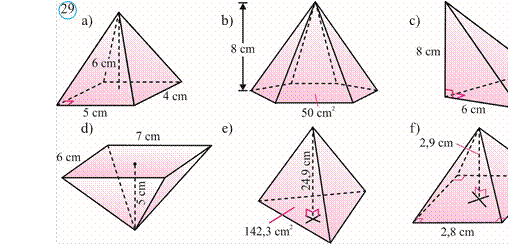
388. 29rasmda berilgan ma’lumotlar asosida piramidalarning hajmini toping.
389. Piramidaning asosi – tomonlari 6 cm, 6 cm va 8 cm bo‘lgan teng yonli uchburchak. Hamma yon qirralari 9 cm ga teng. Piramidaning hajmini toping.
390. Uchburchakli piramidaning bitta qirrasi 4 cm ga, qolganlari esa 3 cm ga teng. Piramidaning hajmini toping.
391. 30rasmdagi piramida kubning qanday qismini tashkil qiladi?
392. To‘rtburchakli muntazam piramida yon sirtining yuzi 72 cm2 ga, asosining yuzi esa 64 cm2 ga teng. Piramidaning hajmini toping.
393. To‘rtburchakli muntazam piramida asosining perimetri 12 cm, yon yog‘ining perimetri esa 18 cm ga teng. Piramidaning hajmini toping.
394*. Qirrasi 5 ga teng kub ABC uchburchak tekisligi bilan ikki bo‘lakka bo‘lingan (31rasm). Kichik bo‘lakning hajmini toping.
395*. Qirrasi 6 ga teng kub ABC uchburchak tekisligi bilan ikki bo‘lakka bo‘lingan (31rasm). Katta bo‘lakning hajmini toping.
396. Muntazam piramidaning balandligi 3 ga, yon qirrasi 5 ga teng. Piramidaning hajmini toping.
397*. ABCD tetraedrda AB=BC= 2, ∠ABC= 120°. DA, DB, DC yon qirralar asos tekisligi bilan 60° li burchak tashkil qiladi. Tetraedrning hajmini toping.
398. ABCA1B1C1 prizma hajmi 48 ga teng (32rasm). C1ABC piramida hajmini toping.
399.
![]()
![]()
![]()
![]()
![]() ABCDA1B1C1D1 og‘ma parallelepiped (33rasm). B1ABCD piramida
hajmi 12 ga teng. Parallelepiped hajmini toping.
ABCDA1B1C1D1 og‘ma parallelepiped (33rasm). B1ABCD piramida
hajmi 12 ga teng. Parallelepiped hajmini toping.
400. ABCA1B1C1 prizma hajmi 87 ga teng (34rasm). C1A1BC piramida hajmini toping.
401. Kub yoqlarining o‘rtalari – oktaedrning uchlari (35rasm). Oktaedr hajmi 12 ga teng. Kubning hajmini toping.
402. AK:KB= 2:3. Piramida hajmi 24 ga teng (36rasm). DABC piramida hajmini toping.
403. BM:MA= 2:3, BK=KC (37rasm). DABC piramida hajmining DMBK piramida hajmiga nisbatini toping.
404*. Piramidaning asosi to‘g‘ri to‘rtburchakdan iborat. Piramidaning har bir yon qirrasi a ga teng bo‘lib, ular to‘g‘ri to‘rtburchakning qo‘shni tomonlari bilan α va β burchaklar tashkil etadi. Piramidaning hajmini toping.
405*. Piramidaning asosi – ikkita burchagi α va β ga teng bo‘lgan uchburchakdan iborat. Bu uchburchakka tashqi chizilgan doiraning radiusi R ga teng. Piramidaning yon qirralari uning asos tekisligiga γ burchak ostida og‘gan bo‘lsa, uning hajmini toping.
406. Xeops piramidasi to‘rtburchakli muntazam piramida shaklida bo‘lib, uning asosi tomoni 230 m, balandligi esa 147 m (38rasm). Piramidaning hajmini toping va uni kub metrlarda ifodalang.

407. Oldingi masaladagi berilganlardan foydalanib Xeops piramidasi yon yog‘ining asos tekisligiga og‘ish burchagini toping.
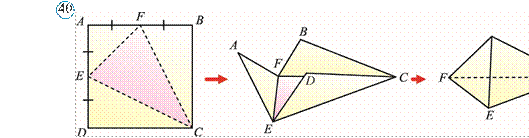
408*. Tomoni 6 cm bo‘lgan kvadrat shaklidagi varaqni 39rasmda ko‘rsatilgandek qilib buklab, uchburchakli piramida hosil qilindi. Bu piramida hajmini toping.
409. Qirrasi 10 cm bo‘lgan kvadrat shaklidagi qog‘ozni 40rasmda ko‘rsatilgandek buklab piramida yasalgan. Rasmda berilgan ma’lumotlar asosida hosil bo‘lgan piramida to‘la sirtini va hajmini toping.
410*. ABCDA1B1C1D1 parallelepipedning hajmi 4,5 ga teng (41rasm). AD1CB1 uchburchakli piramidaning hajmini toping.
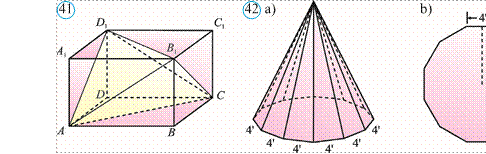
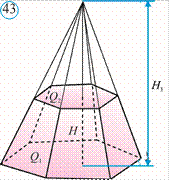
411. Chodir piramida shaklda bo‘lib, u 12 ta tayoqdan qurilgan (42.arasm). Chodirning balandligi 15 fut, asosi esa tomoni 4 futga teng muntazam o‘nikkiburchakdan iborat.Yetishmayotgan kattalikni 42.brasmdan aniqlab, chodirning yon sirti va sig‘imini toping (eslatma: 4 fut 4′ kabi belgilanadi).
10.4. Kesik piramidaning hajmi
![]() Teorema.
Balandligi H, asoslarining yuzi Q1 va Q2 (Q1>Q2) ga teng bo‘lgan
kesik piramidaning hajmi: V
Teorema.
Balandligi H, asoslarining yuzi Q1 va Q2 (Q1>Q2) ga teng bo‘lgan
kesik piramidaning hajmi: V =![]() HQ QQ Q( 1 + 1 2 + 2) ga
teng.
HQ QQ Q( 1 + 1 2 + 2) ga
teng.
 Isbot. Berilgan kesik piramidani to‘liq
piramidagacha to‘ldiramiz (43rasm). H1 bu piramidaning balandligi bo‘lsin. Kesik
piramida hajmi ikkita piramidalar hajmlari ayirmasidan iborat bo‘ladi: V=V1 – V2.
Isbot. Berilgan kesik piramidani to‘liq
piramidagacha to‘ldiramiz (43rasm). H1 bu piramidaning balandligi bo‘lsin. Kesik
piramida hajmi ikkita piramidalar hajmlari ayirmasidan iborat bo‘ladi: V=V1 – V2.
Birinchi piramidaning asosi – Q1, balandligi – H1, ikkinchi piramidaning asosi – Q2, balandligi esa H1 – H ga teng. 117betda isbotlangan teoremaga ko‘ra bu piramidalar o‘xs hash bo‘ladi. Unda 119betda isbotlangan teoremaga ko‘ra quyidagi
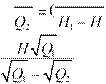 Q1 H1 2 tenglikka
ega bo‘lamiz: )
.
Q1 H1 2 tenglikka
ega bo‘lamiz: )
.
Bu tenglikdan H1 = . (1)
Unda kesik piramidaning hajmi:
![]()
![]()
![]()
3 3 3
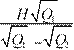 (1) tenglikdan
foydalanib hajmni hisoblasak:
(1) tenglikdan
foydalanib hajmni hisoblasak:
1 1
![]()
![]()
![]() V = 3(Q1 − Q2 )⋅+ Q H2 = 3 H ⋅(Q1 + Q Q1 2 + Q2 ) hosil bo‘ladi.
V = 3(Q1 − Q2 )⋅+ Q H2 = 3 H ⋅(Q1 + Q Q1 2 + Q2 ) hosil bo‘ladi.
10.5. O‘xshash jismlarning hajmlari
F jism berilgan bo‘lib, u shunday F1, F2, ..., Fn uchburchakli piramidalarga ajratilgan bo‘lsinki, F jism hajmi bu piramidalar hajmlari yig‘indisiga teng bo‘lsin. Shunigdek, koeffitsiyentni k ga teng bo‘lgan o‘xshashlik almashtirishi berilgan bo‘lib, F jism bu almashtirishda G jismga o‘tsin.
Unda bu o‘xshashlik almashtirishi F1, F2, ... ,Fn piramidalarni G1, G2, ..., Gn piramidalarga o‘tkazadi va ular o‘z navbatida G jismni tashkil qiladi. Shu bois, G jismning hajmi bu piramidalar hajmlari yig‘indisidan iborat bo‘ladi (44rasm).
Fi va Gi (i=1, 2, ..., n) uchburchakli piramidalar o‘xshash bo‘lgani uchun ularning balandliklari nisbati k ga, asoslarining yuzlari nisbati esa k2 ga teng bo‘ladi. U holda ularning hajmlari nisbati k3 ga teng bo‘ladi.
F jism Fi piramidalardan, G jism Gi piramidalardan (i=1, 2, ..., n) tashkil topgani uchun F va G jismlarning hajmlari nisbati ham k3 ga teng bo‘ladi.
Ma’lumki, k o‘xshashlik almashtirishi koeffitsiyenti F jismning ixtiyoriy ikki nuqtasi orasidagi masofaning bu nuqtalarga mos kelgan G jismning nuqtalari orasidagi masofaga nisbatiga teng. U holda, k soni F va G jismlarning mos chiziqli o‘lchamlari nisbatiga teng bo‘ladi. Shunday qilib, quyidagi xossaga egamiz:
Teorema. Ikki o‘xshash jismning hajmlari nisbati ularning mos chiziqli o‘lchamlari nisbatining kubiga teng.
Xususiy holda, o‘xshash piramidalar uchun (44rasm)
![]() V1 a1 3 3 V1 H1 3 3
V1 a1 3 3 V1 H1 3 3
= ( ) =k , = ( ) = k ,
V a V H
bu yerda a va a1, – o‘xshash piramidalar asosining mos tomonlari, H va H1– balandliklari, V va V1 – hajmlari, k esa o‘xshashlik koeffitsiyenti.
Masala. Piramida balandligining o‘rtasidan asosiga parallel tekislik o‘tkazilgan. Bu tekislik piramida hajmini qanday nisbatda bo‘ladi?
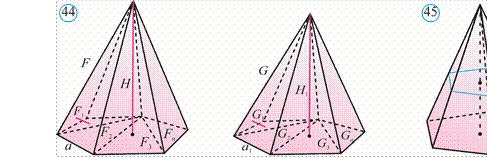
Yechish.
Ma’lumki, o‘tkazilgan tekislik berilgan piramidadan unga o‘xshash
piramidani ajratadi (45 rasm). O‘xshashlik koeffitsiyenti balandliklar
nisbatiga, ya’ni ![]() ta teng.
ta teng.
Shuning uchun piramidalar hajmlari
nisbati ( )![]() : 1 ga teng.
Demak, tekislik piramidani hajmlarining nisbati
: 1 ga teng.
Demak, tekislik piramidani hajmlarining nisbati ![]() bo‘lgan qismlarga
ajratadi.
bo‘lgan qismlarga
ajratadi.
Mavzuga oid masalalar va amaliy topshiriqlar
412. Piramida balandligining o‘rtasidan asosiga parallel tekislik o‘tkazilgan. Hosil bo‘lgan kichik piramida hajmining berilgan piramida hajmiga nisbatini toping.
413. To‘rtburchakli muntazam piramida asosiga parallel tekislik bilan kesilgan (46rasm). Butun va kesik piramida hajmini toping.
414. Asoslarining yuzlari18 dm2 va 8 dm2 va balandligi 6 dm ga teng bo‘lgan kesik piramidaning hajmini toning.
415.
![]()
![]() Asoslarining yuzi 2 2 cm2 va 8 2 cm2, balandligi 9 cm ga
teng bo‘lgan kesik piramidaning hajmini toning.
Asoslarining yuzi 2 2 cm2 va 8 2 cm2, balandligi 9 cm ga
teng bo‘lgan kesik piramidaning hajmini toning.
416. 47rasmda berilgan to‘rtburchakli muntazam kesik piramidaning hajmini toping.
417. 48rasmda berilgan uchburchakli muntazam kesik piramida yuqori asosining tomoni 2 cm bo‘lsa, uning hajmini toping.
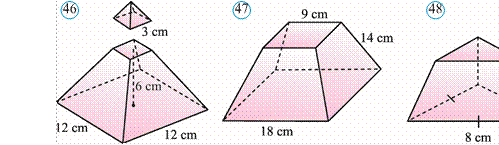
418. 49rasmda berilganlarga ko‘ra kesik piramidaning to‘la sirti va hajmini toping.
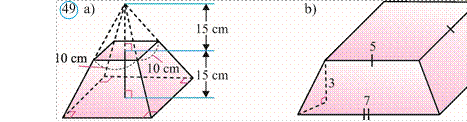
419. 50rasmda berilgan ma’lumotlarga ko‘ra ko‘pyoqlarning hajmini toping va cm3 larda ifodalang. (Eslatma: 6 duym 6′′ kabi belgilanadi va 2, 83 cm ga teng.)
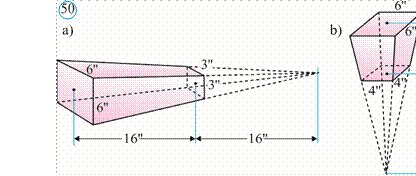
420*. To‘rtburchakli muntazam kesik piramidaning pastki va ustki asoslarining tomonlari a va b ga, pastki asosi qirrasidagi ikki yoqli burchak α ga teng. Piramidaning hajmini toping.
11.1. Konus va uning sirti
Tog‘ri burchakli uchburchakni bir kateti atrofida aylantirishdan hosil bo‘lgan jism konus deb aytiladi (51 rasm). Bu katetni esa konusning o‘qi deb ataymiz. Bu aylantirishda boshqa katet hosil qilgan doira konusning asosi, gipotenuza hosil qilgan sirt esa konusning yon sirti, gipotenuzaning o‘zi esa konusning yasovchisi deb yuritiladi (52rasm).
Konus uchidan uning asos tekisligiga tushirilgan perpendikular konusning balandligi deb ataladi. Konusning o‘qi uning balandligi hamdir.
Eslatma. Tog‘ri burchakli uchburchakni bir kateti atrofida aylantirishdan hosil bo‘lgan jism aslida to‘g‘ri doiraviy konus deb yuritiladi. Konus tushunchasi esa keng ma’noda quyidagicha kiritiladi:
Aytaylik, fazoda berilgan yassi F1 shaklning nuqtalarini unda yotmagan nuqta bilan tutashtiruvchi kesmalardan iborat shakl konus deb ataladi (53 rasm). Berilgan nuqta konusning uchi, berilgan yassi shakl esa konusning asosi deb ataladi.
Agar F1 shakl doiradan iborat bo‘lsa, konus – doiraviy konus deb ataladi (54–55 rasmlar). Doiraviy konus uchini uning asosi markazi bilan tutashtiruvchi kesma konus asosiga perpendikular bo‘lsa, konus – to‘g‘ri, aks holda og‘ma doiraviy konus deb ataladi. Ta’riflangan barcha konuslar ichidan faqat to‘g‘ri doiraviy konusgina aylanma jism bo‘ladi. Biz kelgusida ana shu to‘g‘ri doiraviy konuslar bilan ish ko‘ramiz va ularni qisqalik uchun konuslar deb ataymiz.
Konus o‘qidan o‘tuvchi tekislik bilan kesilganda hosil bo‘lgan kesim o‘q kesim deb ataladi. Konusning barcha o‘q kesimlari teng yonli uchburchaklardir. Konus o‘qidan o‘tuvchi har qanday tekislik uning simmetriya tekisligi bo‘ladi. Konusning simmetriya markazi yo‘q.
56.a rasmda berilgan konus yon sirtini biror yasovchisi bo‘ylab kesib yoysak, uning doiraviy sektordan iborat yoyilmasi hosil bo‘ladi (56.brasm). Yoyilma asosida quyidagi formulalarni osongina keltirib chiqarish mumkin:
Konusning yon sirti uning asosi aylanasi uzunligining yarmi va yasovchisining ko‘paytmasiga teng: Syon= π r l.
Konusning to‘la sirti uning yon sirti va asosining yuzi yig‘indisiga teng: Sto‘la= Syon+ Sasos.
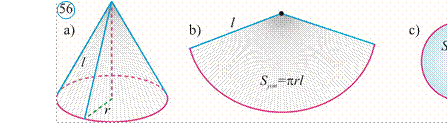
Sto‘la= Syon+ Sasos = πrl + πr2 = πr (r + l).
11.2. Konusning hajmi
Ixtiyoriy konus berilgan bo‘lsin. Uning asosiga ichki A1A2…An1An ko‘pburchakni chizamiz. Ko‘pburchakning A1, A2, …, An–1 va Anuchlarini konusning uchi S nuqta bilan tutashtiramiz. Natijada SA1 A2 … An–1 An piramidani hosil qilamiz. Bu piramida berilgan konusga ichki chizilgan piramida deb ataladi (57rasm). Konus esa piramidaga tashqi chizilgan konus deb yuritiladi. Agar piramida konusga ichki chizilgan bo‘lsa, uning asosi konus asosiga ichki chizilgan bo‘ladi va piramidaning yon qirralari konus yon sirtida yotadi.
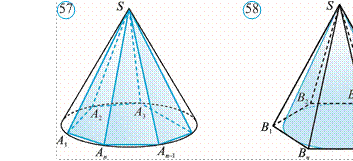
Ravshanki, agar piramida asosiga tashqi aylana chizish mumkin bo‘lsa, bu piramidaga tashqi konus ham chizish mumkin.
Shunga o‘xshash konusga tashqi chizilgan piramida va piramidaga ichki chizilgan konus tushunchalari ham kiritiladi (58rasm). Agar piramida konusga tashqi chizilgan bo‘lsa, unda piramidaning asosi konus asosiga tashqi chizilgan bo‘ladi va piramidaning yon yoqlari konus yon sirtiga urinadi.
Ravshanki, agar piramida asosiga ichki aylana chizish mumkin bo‘lsa, bu piramidaga ichki konus ham chizish mumkin.
Teorema. Konusning hajmi asosining yuzi bilan
balandligi ko‘paytmasining uchdan biriga teng (59-rasm): V = ![]() Sasos
Sasos ⋅ H .
Isbot. Uchi O nuqtada va balandligi H ga teng bo‘lgan konus berilgan bo‘lsin (59.arasm).
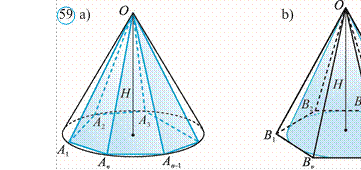
Unga ichki OA1A2…An–1An (59.arasm) va tashqi OB1B2…Bn–1Bn (59.brasm) piramidalarni chizamiz. Konus hajmini V, ichki va tashqi chizilgan piramidalar hajmini V1 va V2 bilan belgilasak, unda V1<V<V2 qo‘shtengsizlik o‘rinli bo‘ladi. Piramidalar hajmi quyidagi formulalardan topiladi:
V1 = ![]() SAA A A1 2.... n−1 n ⋅ H va V
SAA A A1 2.... n−1 n ⋅ H va V![]() SBB B B1 2... n−1 n ⋅ H .
Piramidalar asosi tomonlari soni n ni borgan sari oshirib boramiz. Unda
ichki chizilgan piramida hajmi oshib boradi, tashqi chizilgan piramidaning
hajmi esa kamayib boradi. Agar tomonlar soni n cheksiz kattalashib borsa,
bu hajmlar orasidagi farq nolga intiladi. Konusga ichki va tashqi chizilgan
piramidalar hajmi yaqinlashgan son berilgan konusning hajmi sifatida olinadi.
SBB B B1 2... n−1 n ⋅ H .
Piramidalar asosi tomonlari soni n ni borgan sari oshirib boramiz. Unda
ichki chizilgan piramida hajmi oshib boradi, tashqi chizilgan piramidaning
hajmi esa kamayib boradi. Agar tomonlar soni n cheksiz kattalashib borsa,
bu hajmlar orasidagi farq nolga intiladi. Konusga ichki va tashqi chizilgan
piramidalar hajmi yaqinlashgan son berilgan konusning hajmi sifatida olinadi.
Bu jarayonda A1 A2 … An–1 An va B1 B2 … Bn–1 Bn ko‘pburchaklar yuzi konus asosida yotgan doira yuzi S ga yaqinlashadi.
Demak, V = ![]() Sasos ⋅ H .
Sasos ⋅ H .![]()
Agar konus asosining radiusi r
ga teng bo‘lsa, konus hajmi V = ![]() pr H2 bo‘ladi.
pr H2 bo‘ladi.
Masala. Asosi a ga, asosidagi burchagi α ga teng bo‘lgan teng yonli uchburchakni yon tomoni atrofida aylantirishdan hosil bo‘lgan jismning hajmini toping.
Yechish: ABC teng yonli (AB=AC) uchburchakni AC yon tomoni atrofida aylantiraylik (60rasm). Hosil bo‘lgan jismning V hajmi ikkita konus V1,V2 hajmlarining yig‘indisiga teng.
Birinchi konusning uchi A nuqtada, ikkinchisiniki esa C nuqtada joylashgan.
Har bir konus asosining radiusi ABC uchburchakning BD balandligiga teng.
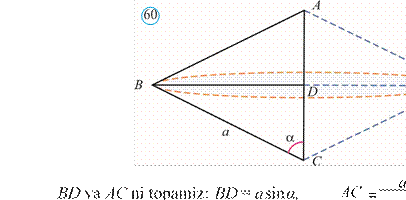
2cosa Konusning hajmi formulasiga ko‘ra
![]()
![]() V1 = π· BD2 · AD, V2 = π· BD2· DC.
V1 = π· BD2 · AD, V2 = π· BD2· DC.
U holda V = V1 + V2=![]() π
·BD2·AD
+
π
·BD2·AD
+![]() π · BD2·DC =
π · BD2·DC =![]() π ·BD2·
(AD + DC) =
π ·BD2·
(AD + DC) =
= ![]() π· BD2· AC =
π· BD2· AC = ![]() π · a2 sin2α ·
π · a2 sin2α · ![]() = π α3 sin2α / 6cosα.
= π α3 sin2α / 6cosα.
Javob: π
a3sin2α / 6 cosα.
![]()
Mavzuga oid masalalar va amaliy topshiriqlar
421. Konusning yasovchisi 13 cm, asosi aylanasining diametri 10 cm. Konusning balandligini toping.
422. Konus asosi aylanasining radiusi 4 cm, balandligi 6 cm bo‘lsa, uning yasovchisini toping.
423. Konus asosi aylanasining diametri 9,6 cm, yasovchisi 5,2 cm bo‘lsa, uning balandligini toping.
424. Konus yasovchisi 12 cm, balandligi esa asosi aylanasining radiusidan 3 marta uzun bo‘lsa, bu radiusni toping.
425. Konus asosi aylanasining radiusni 6 cm, balandligi esa yasovchisidan ikki marta qisqa bo‘lsa, konus yasovchisini toping.
426. Konus asosining diametri 12 cm, yasovchisi esa 10 cm. Konus to‘la sirtining yuzini hisoblang.
427. Konus asosining radiusi 16 cm, konusning balandligi esa 12 cm. Konus yon sirtining yuzini hisoblang.
428. 61rasmda berilganlarga ko‘ra konusning to‘la sirti va hajmini toping.
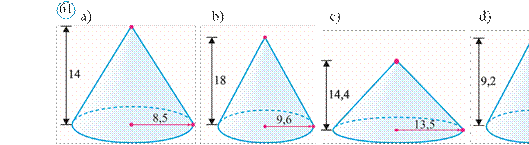
429. 62rasmda berilgan konus yon sirti yoyilmasiga ko‘ra, uning to‘la sirti va hajmini toping.
430. 63rasmda berilganlarga ko‘ra konusning to‘la sirti va hajmini toping.
431. 64rasmda berilgan konus yoyilmasiga ko‘ra uning hajmini toping.
432. 65rasmda berilgan konus yoyilmalariga ko‘ra ularning hajmlari nisbatini toping.
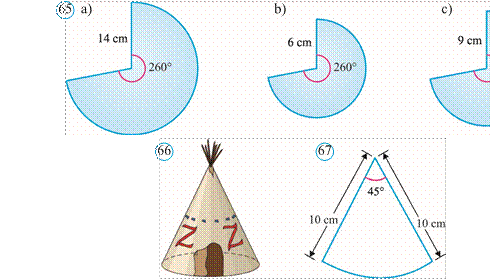
433*. Hindular chodiri konus shaklida bo‘lib, uning asosi radiusi 6 futga, balandligi esa 15 futga teng (66rasm). Chodir yon sirtining yuzini va hajmini toping hamda ularni, mos ravishda, kvadrat metr va kub metrlarda ifodalang.
Ma’lumot: 1 fut (foot) ingliz o‘lchov birligi bo‘lib, qiymati taqriban 30,48 cm ga teng. Shuningdek, u boshqa o‘lchov birliklari bilan quyidagi munosabatlar orqali bog‘langan: 1 fut = 12 duym (inches), 1 duym = 2,54 cm, 1 yard (yard) = 3 fut = 36 duym = 91, 44 cm.
434*. Yon sirti yoyilmasi 67rasmda tasvirlangan doira sektoridan iborat konus hajmini toping.
435. Quyidagi 68rasmda tasvirlangan geometrik jismlar hajmini toping.
436*. Tomoni a ga teng bo‘lgan muntazam oltiburchakni o‘z tomonlaridan biri atrofida aylantirishdan hosil bo‘lgan jismning hajmini toping.
437*. Konus shaklidagi idishdagi sath balandligi 12 cm bo‘lgan suv boshqa silindr shaklidagi idishga quyildi (69rasm). Agar konus va silindr shaklidagi idishlar asoslarining radiusi birbiriga teng bo‘lsa, ikkinchi idishga quyilgan suv sathi qancha bo‘ladi?
438. Silindrdan konus 70rasmda ko‘rsatilgandek o‘yib olingan. Agar silindr asosining radiusi 6 cm va balandligi 8 cm bo‘lsa, hosil bo‘lgan jismning hajmini toping.
439*. 71rasmda berilgan ma’lumotlardan foydalanib, tasvirlangan fazoviy jismlar hajmini toping.
440. Konus asosining diametri 16 cm, konusning balandligi 6 cm. Konus to‘la sirtining yuzini hisoblang.
441. Konus yon sirtining yuzi 65 π dm2, konusning yasovchisi esa 12 cm. Konusning hajmini hisoblang.
442. Konus o‘q kesimining konus uchidagi burchagi 120° ga teng. Agar konus uchidan o‘tuvchi boshqa kesimning konus uchidagi bur chagi 90° bo‘lib, konus asosining radiusi 12 cm bo‘lsa, bu kesimning yuzini hisoblang.
443. Konusning o‘q kesimi – teng tomonli uchburchak bo‘lib, balandligi 9 cm ga teng. Konusning uchi orqali uning asosi markazidan 3 cm masofada o‘tuvchi kesimning yuzini hisoblang.
444. Katetlari 12 cm va 16 cm bo‘lgan to‘g‘ri burchakli uchburchak kichik katet atrofida aylanadi. Hosil bo‘lgan aylanma jism to‘la sirtining yuzini hisoblang.
445. Konus yon sirtining yuzi 32 π ga teng, uning yasovchisi asos tekisligiga 60° li burchak ostida og‘gan. Konusning hajmini hisoblang.
446. Konus o‘q kesimining perimetri 24 cm, yon sirti yoyilmasining burchagi 120° ga teng. Konus to‘la sirtining yuzini hisoblang.
447*. Konusda ikkita o‘zaro perpendikular yasovchilar orqali o‘tkazilgan kesimning yuzi 18 cm2. Uning asosidagi kesimga mos vatar 120° li yoyni tortib turadi. Konusning hajmini hisoblang.
448. 72rasmda katta konusga kichik konus ichki chizilgan, bunda kichik konus uchi katta konus asosining markazida yotadi va kichik konus balandligi kattasinikidan ikki marta kichik. Katta konus hajmining kichik konus hajmiga nisbatini toping.
449*. 73rasmda ko‘rsatilgan shaklni Ox o‘qi atrofida aylantirishdan hosil bo‘lgan jismning hajmini toping.
450*. 74 rasmda ko‘rsatilgan shaklni Ox o‘qi atrofida aylantirishdan hosil bo‘lgan jism sirtining yuzini toping.
451*. Uchlari Oxy tekisligining (0; 0), (5; 0) va (0; 9) nuqtalarda bo‘lgan to‘g‘ri burchakli uchburchakning a) Ox; b) Oy o‘qi atrofida aylanishidan hosil bo‘lgan fazoviy jismning to‘la sirtini va hajmini toping.
452*. Uchlari Oxy tekisligining (0; 0), (6; 0) va (6; 4) nuqtalarda bo‘lgan to‘g‘ri burchakli uchburchak a) Ox; b) Oy o‘qi atrofida aylanishidan hosil bo‘lgan fazoviy jismning to‘la sirtini va hajmini toping.
453. Konusga balandligi konus balandligidan 2 marta kichik bo‘lgan silindr ichki chizilgan. Konusning hajmi 48 ga teng (75rasm). Silindr hajmini toping.
454. Konus asosining yuzi 40 ga, yasovchisi asos tekisligi bilan 60°li burchak tashkil qiladi (76rasm). Konus yon sirtining yuzini toping.
11.3. Kesik konus va uning sirti
Konusni uning asos tekisligiga parallel va uni kesib o‘tadigan tekislik bilan kesamiz. Natijada u ikki bo‘lakka ajraladi. Ulardan biri mazkur konusga o‘xshash bo‘lgan konusdan, ikkinchisi esa kesik konus deb ataluvchi jismdan iborat bo‘ladi (77rasm). Kesik konus ikkita doira – kesik konusning asoslari va yon sirti bilan chegaralangan (78rasm).
Kesik konusni to‘g‘ri burchakli trapetsiyaning ki chik yon tomoni atrofida aylanishidan hosil bo‘lgan jism sifatida ham qarash mumkin (79rasm).
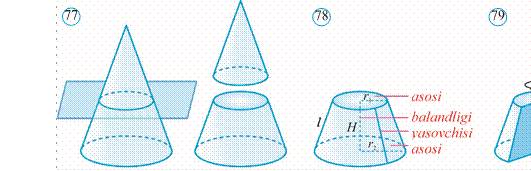
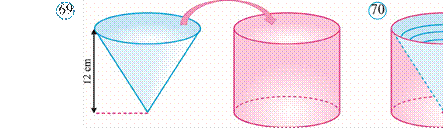
Kesik konusning balandligi uning ikki asosi orasidagi masofaga teng bo‘ladi.
Kesik konus yon sirtining yuzi quyidagi formula yordamida hisoblanadi:
S yon = π l (r1+ r2),
bu yerda l, r1, r2, mos ravishda, konusning yasovchisi va asoslarining radiuslari (78rasm).
Kesik konusning to‘la sirti uning yon sirti va asoslari yuzi yig‘indisiga teng:
S to‘la = S yon + π r12 + π r22 = π l (r1+ r2) + π r12 + π r22.
S to‘la = π (r12 + π r22 + l (r1+ r2)).
11,4, Kesik konusning hajmi
Teorema. Balandligi H, asoslarining yuzi S1 va S2 (S1 > S2) ga teng bo‘l-
1
![]() gan kesik konusning
hajmi V
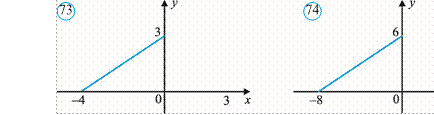
gan kesik konusning
hajmi V
= H S( 1 + SS S1 2 + 2) ga teng (80-rasm).
3
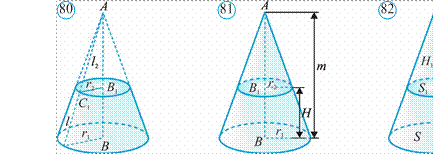
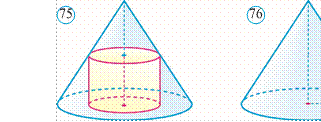
Isbot. Berilgan kesik konusni to‘liq konusgacha to‘ldiramiz (81rasm). m bu konusning balandligi bo‘lsin. Kesik konusning hajmi ikkita konuslar hajmlari ayirmasidan iborat bo‘ladi.
Birinchi konusning asosi – S1, balandligi – m, ikkinchi konusning asosi –
S2, balandligi esa m–H ga teng. Bu konuslarning o‘xshashligidan quyidagi
![]()
 S1 m 2 . Bu
tenglikdan m= tenglikka ega bo‘lamiz: = ( )
S1 m 2 . Bu
tenglikdan m= tenglikka ega bo‘lamiz: = ( )
S2 m− H
Unda kesik konusning hajmi:
V =V1 −V2 = ![]() S1 ⋅m −
S1 ⋅m − ![]() S2 ⋅(m − H) =
S2 ⋅(m − H) = ![]() (S1 − S2 )m + S H2 ) . m=
(S1 − S2 )m + S H2 ) . m=
3 3 3
![]() o‘rniga
qo‘yib hajmni hisoblasak, V H S SS S
o‘rniga
qo‘yib hajmni hisoblasak, V H S SS S
Agar kesik konus asoslarining radiusi
r1 va r2 ga teng bo‘lsa, kesik
konusning hajmi: V =![]() π
H (r12 + r1r2 + r22) ga teng
bo‘ladi.
π
H (r12 + r1r2 + r22) ga teng
bo‘ladi.
Shuningdek, oldingi paragrafda piramidalar uchun ifodalangan xossa konuslar uchun o‘rinli bo‘ladi:
Teorema. Hajmi V, balandligi H va asosining yuzi S ga teng bo‘lgan konus asosiga parallel tekislik bilan kesilganda, hajmi V1, balandligi H1 va asosining yuzi S1 ga teng bo‘lgan konus hosil bo‘lgan bo‘lsin (82-rasm).
![]()
![]() S1 H1 2 2 V H1 1 3
S1 H1 2 2 V H1 1 3
U
holda = ( ) =k , = ( ) =k3
S H V H
bu yerda k – konuslarning o‘xshashlik koeffitsiyenti. Mavzuga oid masalalar va amaliy topshiriqlar
455. Kesik konus asoslarinning diametrlari, mos ravishda, 16 cm va 10 cm, balandligi esa 4 cm. Kesik konus yon sirtining yuzini hisoblang.
456. Kesik konus asoslarining radiuslari 12 cm va 8 cm, yasovchisi esa katta asos tekisligiga 60° li burchak ostida og‘gan. Kesik konus yon sirtining yuzini hisoblang.
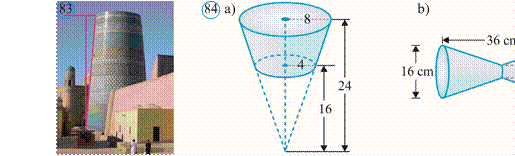
457. Xiva shahridagi Kalta Minor kesik konus shaklida bo‘lib, uning pastki asosi diametri 14,2 m va balandligi 29 m ni tashkil qiladi (83rasm).
Minoraning yasovchisi balandligi bilan 15° li burchak hosil qiladi. Minora yon sirtining yuzini toping.
458. Kesik konus asoslarining radiuslari, mos ravishda, 8 cm va 5 cm, yasovchisi asos tekisligiga 45° li burchak ostida og‘gan. Kesik konusning hajmini hisoblang.
459. Kesik konus yuqori va pastki asoslarining radiuslari 18 cm va 10 cm, o‘q kesimining diagonallari o‘zaro perpendikular. Kesik konusning hajmini hisoblang.
460. Kesik konusning yasovchisi 10 cm va asos tekisligiga 60° li burchak ostida og‘gan, o‘q kesimining diagonali bu burchakni teng ikkiga bo‘ladi. Kesik konusning hajmini hisoblang.
461*. 84rasmda tasvirlangan geometrik jismlar hajmini toping.

462*. Osiyoning ko‘plab xalqlari qadimdan o‘tovlarda yashab kelishgan. 85 rasmda zamonaviy o‘tovlardan biri tasvirlangan. O‘tov devorlari silindr, tomi esa kesik konus yon sirtlaridan iborat. O‘tovning balandligi 3,5 m, devorlari balandligi 1,7 m va asosining diametri 6,83 m ni tashkil qiladi. Yetishmayotgan kattalikni rasmdan chamalab aniqlab, o‘tov devorlari va tomini qoplash uchun necha kvadrat metr kigiz materialidan kerak bo‘lishini hamda o‘tovning sig‘imini toping.
463*. Uchlari Oxy tekisligining (2; 0), (4; 0) va (2; 4) nuqtalarda bo‘lgan to‘g‘ri burchakli uchburchakning Oy o‘qi atrofida aylanishidan hosil bo‘lgan fazoviy jismning hajmini toping (86 rasm).
464*. Oxy tekisligining birinchi choragida joylashgan, koordinata o‘qlari, x=9 va y=5 to‘g‘ri chiziqlar bilan chegaralangan to‘g‘ri to‘rtburchakning a) Ox; b) Oy o‘qi atrofida aylanishidan hosil bo‘lgan fazoviy jismning to‘la sirtini va hajmini toping.

465. Yogurt qutisi kesik konus shaklida bo‘lib (87rasm), uning katta asosining diametri 8 cm, kichik asosining diametri 6 cm, balandligi esa 7,5 cm. Qutining hajmini toping.
466.
Qaymoq idishi
kesik konus shaklida bo‘lib (88rasm), uning katta asosining diametri 14 cm,
kichik asosining diametri 11 cm, balandligi esa 6 ![]() cm. Qutining hajmini toping.
cm. Qutining hajmini toping.
467*. Yog‘ochdan ishlangan kesik konusdan 89rasmda ko‘rsatilgandek qilib silindr o‘yib olingan. Hosil bo‘lgan jism sirtini va hajmini toping.
468*. Silindr ichiga joylashtirilgan konuslar hajmi nisbati 1:2 bo‘lsa (90rasm), silindrning bo‘sh qolgan qismining hajmini toping.
469. To‘g‘ri burchakli parallelepipedga ichki chizilgan konus hajmini toping (91rasm).
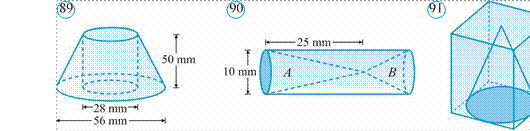
470*. Asosining o‘lchamlari 10 cm va 12 cm bo‘lgan to‘g‘ri burchakli parallelepiped shaklidagi sut qutisida 1200 cm3 hajmdagi sut bor (92rasm). Sut qutisi asosining yuzi 80 cm2 bo‘lgan silindr shaklidagi stakanga to‘ldirib quyilganda, idishlardagi sut sathlari teng bo‘lib qoldi. Stakanning hajmini toping.
471. 93rasmda berilganlarga ko‘ra raketaning to‘la sirti va hajmini toping.
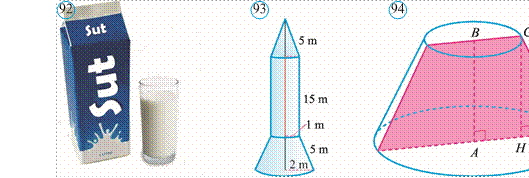
![]() 472*. ABCD trapetsiyada
472*. ABCD trapetsiyada ![]() A=90°,
A=90°, ![]() D= 45°, BC = 5 cm, CD = 3 2 cm (94rasm). Bu trapetsiyaning AB
tomoni atrofida aylanishidan hosil bo‘lgan kesik konusning yon sirti va hajmini
toping.
D= 45°, BC = 5 cm, CD = 3 2 cm (94rasm). Bu trapetsiyaning AB
tomoni atrofida aylanishidan hosil bo‘lgan kesik konusning yon sirti va hajmini
toping.
473*. ABCD trapetsiyada ![]() A = 90°,
A = 90°,
![]() D = 60°, BC = 4 cm, CD
= 12 cm. Bu trapetsiyaning AB tomoni atrofida aylanishidan hosil bo‘lgan
kesik konusning yon sirti va hajmini toping.
D = 60°, BC = 4 cm, CD
= 12 cm. Bu trapetsiyaning AB tomoni atrofida aylanishidan hosil bo‘lgan
kesik konusning yon sirti va hajmini toping.
474*. Kesik konusga uchburchakli muntazam kesik piramida ichki chizilgan, ya’ni piramida asoslari kesik konus asoslariga ichki chizilgan (95rasm). Kesik konus asoslarining radiuslari 2 cm va 5 cm, balandligi esa 4 cm ga teng. Piramidaning to‘la sirtini toping.
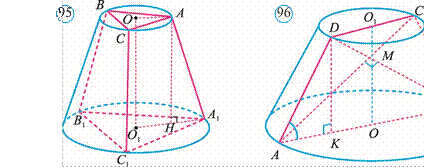
475*. Kesik konusda o‘q kesim diagonallari o‘zaro perpendikular bo‘lib, katta asos tekisligi bilan 60° li burchak tashkil qiladi va 4 cm ga teng (96rasm). Kesik konus hajmini toping.
AlXorazmiyning “Al jabr valmuqobala hisobi haqida” nomli asarining o‘lchash haqidagi bobida kesik piramidaning hajmini hisoblashga oid quyidagi ma’lumotlar keltirilgan:“Agar piramidaning pastki asosi to‘rt gazga to‘rt gaz, balandligi o‘n gaz va uning yuqori asosi ikki gazga ikki gaz deyilsa, u holda, bizga ma’lumki, har bir o‘tkir uchli piramida shunday bo‘ladiki, uning asosi yuzining uchdan birining balandligiga ko‘paytmasi uning hajmidir. Shuning uchun bu piramidaning uchi bo‘lmaganligi sababli, biz uning uchini tiklash uchun qanchalik ko‘tarish kerak ekanligini bilmoqchimiz. Uning uchi yo‘q, lekin bu o‘n gazning uning butun uzunligiga nisbati, ikkining to‘rtga nisbati ekanligini bilamiz. Biroq ikki – to‘rtning yarmi, shuning uchun, agar nisbat shunday bo‘lsa, u holda o‘n uzunlikning yarmi va (demak) uzunlik – yigirma gaz. Shunday qilib, biz uzunlikni bilamiz. Asosning uchdan birini, ya’ni beshu uchdan birni olamiz, buni uzunlikka, ya’ni yigirma gazga ko‘paytiramiz; buning ko‘paytmasi bir yuz oltiyu uchdan ikki gaz. Biz uni (to‘liq) piramidagacha to‘ldirish uchun qo‘shganimizni, undan (o‘lchami) ikkiga ikki bo‘lgan yuzaning uchdan birini o‘nga qo‘shganimizni yoki o‘n uchu uchdan birni ya’ni to‘liq piramida hosil qilish uchun biz qo‘shgan hajmni ayiramiz. Agar biz buni bir yuz oltiyu uchdan ikki gazdan ayirsak, to‘qson uchu uchdan bir qoladi. Ana shu piramidaning hajmidir”.
Abu Ali ibn Sino “Donishnoma” asarining o‘n ikkinchi bobida geometrik jismlar haqida fikr yuritadi. Jumladan, uchburchakli piramidani ikkita o‘zaro teng, berilgan piramidaga o‘xshash piramidalarga hamda ikkita teng prizmalarga ajratish usulini bayon qilgan.
3test topshirig‘i
1. To‘rtburchakli muntazam piramidaning balandligi 6 cm, apofemasi esa 6,5 cm. Piramida asosining perimetrini toping.
A) 10 cm; B) 12 cm; C) 24 cm; D) 20 cm.
2. Muntazam piramida yon sirtining yuzi 96 ga, asosining perimetrini 24 ga teng. Piramidaning apofemasini toping.
A) 16; B) 10; C) 6; D) 8.
3. Uchburchakli muntazam piramidaning balandligi 4 ga, asosining balandligi esa 4,5 ga teng. Piramidaning yon qirrasini toping.
A) 6; B) 6,5; C) 5; D) 5,5.
4. To‘rtburchakli muntazam piramidaning balandligi 24 ga, asosining tomoni esa 14 ga teng. Uning apofemasini toping.
A) 18; B) 27; C) 25; D) 32.
5. Muntazam piramidaning asosi ichki burchaklarining yig‘indisi 720° ga, tomoni 6 ga teng bo‘lgan ko‘pburchakdan iborat. Agar piramidaning yon qirrasi 10 ga teng bo‘lsa, piramidaning balandligini toping.
A) 8; B) 6; C) 9; D) 7.
6. Oktaedrning qirrasi a ga teng. Uning to‘la sirtini hisoblang.
![]()
![]()
![]()
![]() A)
2a2 3 ; B)
a2 3 ; C) 2 3a2 /3;
D) 4a2 3 .
A)
2a2 3 ; B)
a2 3 ; C) 2 3a2 /3;
D) 4a2 3 .
7. Muntazam tetraedrning qirrasi 1 ga teng. Uning asosiga tashqi chizilgan aylananing markazidan uning yon yog‘igacha bo‘lgan masofani toping.
![]()
![]()
![]()
![]() A)
2 3 /6;
B) 6 /9; C) 2 2 /5; D) 3 6 / 8.
A)
2 3 /6;
B) 6 /9; C) 2 2 /5; D) 3 6 / 8.
8. Muntazam piramidaning yon sirti 24 ga, asosining yuzi 12 ga teng. Piramidaning yon yog‘i bilan asos tekisligi orasidagi burchakni toping.
A) 45°; B) 30°; C) 60°; D) 35°.
9. To‘rtburchakli muntazam piramida asosining tomoni 4 marta kattalashtirildi, balandligi esa 4 marta kichiklashtirildi. Hosil bo‘lgan piramida hajmining dastlabki piramida hajmiga nisbatini toping.
A) 1 : 16; B) 16 : 1; C) 1 : 1; D) 4 : 1.
10. To‘rtburchakli muntazam piramidaning hajmi 48 ga, balandligi esa 4 ga teng. Piramida yon sirtining yuzini toping.
A) 120; B) 144; C) 60; D) 96.
11. Qirrasi 1 ga teng bo‘lgan kub yoqlarining markazlari tutashtirildi. Hosil bo‘lgan jismning hajmini toping.
A) ![]() ; B)
; B) ![]() ;
C)
;
C) ![]() ; D)
; D) ![]() .
.
12. Parallelepiped ostki asosining diagonali va ustki asosining bu diagonalga qaramaqarshi uchi orqali tekislik o‘tkazilgan. Bu tekislik parallelepipedni ikkita jismga ajratadi. Shu jismlardan biri piramidadan iborat. Parallelepiped hajmining piramida hajmiga nisbatini toping.
A) 5 : 1; B) 6 : 1; C) 3 : 1; D) 4 : 1.
13. SABC piramidaning SBC yon yog‘ining yuzi 60 ga teng. Bu yon yoq A uchidan 8 ga teng masofada joylashgan. Piramidaning hajmini toping.
A) 170; B) 150; C) 120; D) 180; E) 160.
14. To‘rtburchakli muntazam piramidaning balandligi 9 ga, diagonal kesimning yuzi 36 ga teng. Piramidaning hajmini toping.
A) 84; B) 96; C) 48; D) 72.
15. Qirrasining uzunligi a ga teng bo‘lgan muntazam tetraedrning hajmini toping.
![]()
![]()
![]() A)
A) ![]() a3 2 ; B)
a3 2 ; B) ![]() a3; C)
a3; C)
![]() a3 3; D)
a3 3; D) ![]() a3 3 .
a3 3 .
16. Quyida keltirilgan parallelogrammlarning qaysilari barcha yon yoqlari asos tekisligi bilan bir xil burchak tashkil qiladigan piramidaning asosi bo‘lishi mumkin?
A) ixtiyoriy parallelogramm; B) faqat kvadrat;
C) romb yoki kvadrat; D) faqat to‘g‘ri to‘rtburchak.
17. To‘rtburchakli muntazam kesik piramida asoslarining tomonlari 3 cm va 7 cm, diagonali 10 cm. Kesik piramidaning balandligi necha cm?
![]()
![]() A)
5; B) 5 2 ; C) 4 2 ; D) 4.
A)
5; B) 5 2 ; C) 4 2 ; D) 4.
18. To‘rtburchakli muntazam kesik piramidaning diagonallari o‘zaro perpendikular va ularning har biri 8 ga teng. Piramidaning balandligini toping.
![]()
![]() A)
4 2 ; B)
2 2 ; C)
4; D) 6.
A)
4 2 ; B)
2 2 ; C)
4; D) 6.
19. ![]() Konus asosining radiusi 1/ 3 ga teng. Konus
yasovchisi bilan uning asos tekisligi orasidagi burchak qanday bo‘lganda konus
yon sirtining yuzi π/ 3 ga teng bo‘ladi?
Konus asosining radiusi 1/ 3 ga teng. Konus
yasovchisi bilan uning asos tekisligi orasidagi burchak qanday bo‘lganda konus
yon sirtining yuzi π/ 3 ga teng bo‘ladi?
A) 30°; B) 60°; C) 45°; D) arccos (1/3).
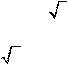
20. Konus asosining radiusi 6 ga teng, yasovchisi asos tekisligi bilan 30° li burchak tashkil etadi. Asos markazidan yasovchigacha bo‘lgan masofani toping.
 A)
4; B) 3; C) 2,5; D)
3 3 .
A)
4; B) 3; C) 2,5; D)
3 3 .
21. Konusning yasovchisi asos tekisligi bilan 45° li burchak tashkil etadi.
Asosning markazidan yasovchisigacha bo‘lgan masofa 3 2 ga teng. Konusning balandligini toping.
A) 5; B) 4; C) 7; D) 6; 5.
22. Konusning yasovchisi 12 ga teng va u asos tekisligi bilan 60° li burchak hosil qiladi. Konus asosining radiusini toping.
A) 12; B) 6; C) 3; D) 2.
23. Konus o‘q kesimining yuzi 8 ga, asosining radiusi 2 ga teng. Konus yon sirtining yuzini hisoblang.
![]()
![]() A)
6π; B) 4 5 π; C) 5 5 π; D) 5π.
A)
6π; B) 4 5 π; C) 5 5 π; D) 5π.
24. Konusning yon sirti tekislikka yoyilganda, yoyilmaning uchidagi burchak 30° ga teng bo‘ldi. Konus yasovchisining asos radiusiga nisbatini toping.
A) 10; B) 12; C)11; D) 9.
25. Konusning balandligi 8 ga, asosining radiusi 6 ga teng. Konus yoyilmasining uchidagi burchakni aniqlang.
A) 216°; B) 270°; C)180°; D) 312°.
26. Asosining radiusi R ga teng bo‘lgan konusning yon sirti asosi bilan o‘q kesimi yuzlarining yig‘indisiga teng. Konusning hajmini toping.
A) 2π2R3/3(π2–1); ![]() B)
πR3/2(π2+1);
B)
πR3/2(π2+1); ![]() C) 2(π2+1)/πR3;
C) 2(π2+1)/πR3; ![]() D) π(π2+1)/3.
D) π(π2+1)/3.
27. Konusning o‘q kesimi teng tomonli uchburchakdan, silindrniki esa kvadratdan iborat. Agar ularning to‘la sirtlari teng bo‘lsa, hajmlarining nisbatini toping.
![]()
![]() A)
2 : 3; B) 1 : 3; C) 1 : 2 ; D) 2 .
A)
2 : 3; B) 1 : 3; C) 1 : 2 ; D) 2 .
28. Konusning yasovchisi 6 ga teng va u asos tekisligi bilan 30° li burchak hosil qiladi. Konusning hajmini toping.
![]()
![]() A) 9π; B)
9 3 π;
C) 27π; D) 27 3 π.
A) 9π; B)
9 3 π;
C) 27π; D) 27 3 π.
29. y = |x + 2|, x = –3, x = 0 va y = 0 chiziqlar bilan chegaralangan shaklni abssissalari o‘qi atrofida aylantirish natijasida hosil bo‘lgan jismning hajmini toping.
A) 2π; B) 3π; C) π; D) 4π.
30. Yasovchisi 5 ga, balandligi 4 ga teng bo‘lgan konus asosidan 2 ga teng masofada shu asosga parallel tekislik bilan kesildi. Hosil bo‘lgan kesimning yuzini hisoblang.
A) 2,25π; B) 3,16π; C) 2,64π; D) 1,81π.
Masalalar
Piramida to‘la sirtining yuzi
476. To‘rtburchakli muntazam piramidaning uchidagi tekis burchagi 60° ga teng. Shu piramidaning yon qirrasi va asosi orasidagi burchakni toping.
477. Apofemasi 5 ga teng bo‘lgan to‘rtburchakli muntazam piramidaning to‘la sirti 11 dan katta va 24 dan kichik. Piramida asosi tomonining uzunligi qanday oraliqda yotadi?
478. To‘rtburchakli muntazam piramida asosining tomoni 5 ga, to‘la sirti 85 ga teng. Piramida yon yog‘ining asos tekisligiga og‘ish burchagini toping.
479. Piramidaning asosi gipotenuzasi uzunligi 2 bo‘lgan to‘g‘ri burchakli uchburchakdan iborat. Piramidaning qirralari asos tekisligi bilan α burchak tashkil qiladi. Agar uning balandligi 5 ga teng bo‘lsa, tgα ning qiymatini toping.
480. Asosdagi ikki yoqli burchaklari 60° ga teng bo‘lgan piramidaning asosi tomoni 6 ga, o‘tkir burchagi 30° ga teng rombdan iborat. Piramidaning to‘la sirtini toping.
481. Uchburchakli muntazam piramidaning balandligi asosining tomonidan ikki marta kichik. Piramidaning yon yog‘i asos tekisligi bilan qanday burchak tashkil etadi?
482. Uchburchakli muntazam piramida asosining tomoni 10 ga teng. Yon yog‘i asos tekisligi bilan 45° li burchak hosil qiladi. Piramidaning balandligini toping.
483. Uchburchakli muntazam piramidaning yon qirrasi 10 ga, asosining tomoni 12 ga teng. Piramidaning balandligini toping.
484. Piramidaning yon qirralari asosi tekisligi bilan bir xil burchak tashkil etadi. Romb, uchburchak, kvadrat va to‘g‘ri to‘rtburchakdan qaysi biri piramidaning asosi bo‘lolmaydi?
485. Uchburchakli piramidaning asosidagi barcha ikki yoqli burchaklar 30° ga teng. Agar piramidaning balandligi 6 ga teng bo‘lsa, uning asosiga ichki chizilgan doiraning radiusini toping.
486. Uchburchakli piramida asosining tomonlari 9, 10 va 17 ga teng. Piramidaning barcha yon yoqlari asos tekisligi bilan 45° li burchak tashkil etsa, uning hajmini toping.
487. Uchburchakli og‘ma prizma asosining medianasi va shu mediana bilan kesishmaydigan qirraning o‘rtasi orqali bu prizmadan piramida ajratadigan kesim o‘tkazildi. Agar prizmaning hajmi 30 ga teng bo‘lsa, piramidaning hajmini toping.
488.
![]() Oltiburchakli muntazam piramidaning
hajmi 13,5 ga, balandligi esa 3 ga
teng. Shu piramida yon qirrasining asos tekisligi bilan hosil qilgan burchagini
toping.
Oltiburchakli muntazam piramidaning
hajmi 13,5 ga, balandligi esa 3 ga
teng. Shu piramida yon qirrasining asos tekisligi bilan hosil qilgan burchagini
toping.
489. Uchburchakli piramidaning asosi tomonlari 4, 4 va 2 ga teng bo‘lgan uchburchakdan iborat. Piramidaning barcha yon yoqlari asos tekisligi bilan 60° li burchak tashkil etadi. Piramidaning hajmini toping.
490.
![]() Oltiburchakli muntazam piramidaning
hajmi 324 ga, balandligi 6 3 ga
teng. Shu piramidaning yon qirrasi va asos tekisligi orasidagi burchakni
toping.
Oltiburchakli muntazam piramidaning
hajmi 324 ga, balandligi 6 3 ga
teng. Shu piramidaning yon qirrasi va asos tekisligi orasidagi burchakni
toping.
491. Piramidaning asosi kvadratdan iborat. Kvadratning digonali 6 ga teng. Piramidaning yon qirralaridan biri uning asosiga perpendikular. Piramidaning katta yon qirrasi va asos tekisligi orasidagi burchak 45° ga teng. Piramidaning hajmini toping.
492. Uchburchakli muntazam piramidaning yon qirrasi l ga teng va asos tekisligi bilan α burchak hosil qiladi. Piramidaning hajmini toping.
493. To‘rtburchakli muntazam piramidaning hajmi 20 ga, balandligi esa 1 ga teng. Piramidaning apofemasi uzunligini toping.
494. Kesik piramida asoslarining yuzlari 96 va 24 ga, unga mos keluvchi butun piramidaning balandligi 16 ga teng. Kesik piramidaning hajmini toping.
495. Muntazam kesik piramida ustki asosining yuzi ostki asosining yuzidan uch marta kichik. Piramidaning barcha yon yoqlari ostki asosiga 60° li bur chak ostida og‘gan. Piramida ostki asosining yuzi piramida yon sirtining necha foizini tashkil etadi?
496.
![]() Konus o‘q kesimi teng tomoli
uchburchakdan iborat bo‘lib, uning yuzi 16 3 ga teng. Shu konus yon sirtining yuzini toping.
Konus o‘q kesimi teng tomoli
uchburchakdan iborat bo‘lib, uning yuzi 16 3 ga teng. Shu konus yon sirtining yuzini toping.
497. Asosining radiusi R ga teng va o‘q kesimi to‘g‘ri burchakli uchburchakdan iborat konusning yon sirtini toping.
498. Konusning yasovchisi 100 ga, uning asos tekisligi bilan tashkil qilgan burchagining sinusi 0,6 ga teng. Konus o‘q kesimining perimetrini aniqlang.
499. Konus asosining radiusi 12 ga, yasovchisi esa 40 ga teng. Shu konus yoyilmasining uchidagi burchagini toping.
500. Konus asosining radiusi 6 ga, balandligi 8 ga teng. Konus yoyilmasining uchidagi burchagini toping.
501.
![]() Konusning o‘q kesimi muntazam
uchburchakdan iborat. Uchburchakning yuzi 16 3 ga teng. Konusning to‘la sirtini toping.
Konusning o‘q kesimi muntazam
uchburchakdan iborat. Uchburchakning yuzi 16 3 ga teng. Konusning to‘la sirtini toping.
502. Muntazam uchburchakning tomoni 2 ga teng. Shu uchburchakni uchidan o‘tuvchi va qaramaqarshi tomoniga parallel o‘q atrofida aylantirishdan hosil bo‘lgan jismning hajmini toping.
503. Konusning balandligi 12 ga, o‘q kesimining perimetri 36 ga teng. Uning hajmini toping.
504. Konus asosining radiusi 2 ga, yasovchisi va asos tekisligi orasidagi burchak 60° ga teng. Konusning hajmini toping.
505. Teng yonli uchburchakning tomonlari 10 va 22 ga teng. Shu uchburchak o‘zining simmetriya o‘qi atrofida aylantirilganda hosil bo‘lgan aylanish jismining to‘la sirtini toping.
506. Konusning yon sirti 96π ga teng. Shu konus balandligining o‘rtasidan unga perpendikular tekislik o‘tkazish natijasida hosil bo‘lgan kesik konusning yon sirtini toping.
1. Uchburchakli muntazam piramidaning balandligi 4 ga, asosining balandligi esa 4,5 ga teng. Piramidaning yon qirrasini toping.
2.
 To‘rtburchakli
muntazam piramidaning balandligi 15 ga, diagonal kesimining yuzi 120 ga teng.
Shu piramidaning hajmini toping.
To‘rtburchakli
muntazam piramidaning balandligi 15 ga, diagonal kesimining yuzi 120 ga teng.
Shu piramidaning hajmini toping.
3. To‘rtburchakli muntazam kesik piramida asoslarining tomonlari 3 cm va 5 cm, diagonali 9 cm. Kesik piramidaning balandligini toping.
4. Konus asosining radiusi 6 ga, balandligi 8 ga teng. Konus yoyilmasining uchidagi burchagini toping.
5. Rasmda ko‘rsatilgan uchburchakning to‘g‘ri chiziq atrofida aylanishidan hosil bo‘lgan jismning hajmini toping.
|
13. SHAR VA UNING ELEMENTLARI |
![]()
 IV BOB. SFERA VA SHAR
IV BOB. SFERA VA SHAR
Fazoning berilgan nuqtadan, berilgan masofadan katta bo‘lmagan uzoqlikda yotgan hamma nuqtalaridan iborat jismga shar deyiladi. Berilgan nuqta sharning markazi, berilgan masofa esa sharning radiusi deb ataladi (1rasm).
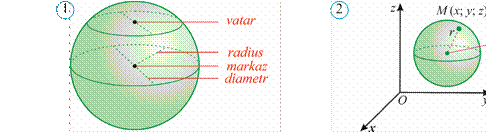
Sharning chegarasi shar sirti yoki sfera deb ataladi. Shunday qilib, sharning markazidan radiusga teng masofa qadar uzoqlashgan hamma nuqtalar sferaning nuqtalaridir. Shar markazini shar sirtining istalgan nuqtasi bilan tutashtiruvchi kesma ham radius deyiladi (1rasm)
Ta’rifga ko‘ra, markazi A (a; b; c) nuqtada va radiusi R ga teng bo‘lgan sfera ning ixtiyoriy M (x; y; z) nuqtasi koordinatalari (x−a)2 +(y−b)2 +(z−c)2=R2 tenglikni qanoatlantiradi (2rasm). Uni sferaning tenglamasi deb yuritamiz. Agar sferaning markazi A (0; 0; 0) nuqtada bo‘lsa, uning tenglamasi x2+ y2+ z2= R2 ko‘rinishni oladi.
Shuningdek, ta’rifga kora, markazi A (a; b; c) nuqtada va radiusi R ga teng bo‘lgan shar M (x; y; z) nuqtalarining koordinatalari
(x−a)2 +(y−b)2 +(z−c)2≤R2 tengsizlikni qanoatlantiradi.
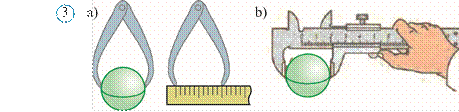
Shar sirtining ikki nuqtasini tutashtiruvchi va sharning markazidan o‘tuvchi kesma diametr deyiladi. 3rasmda shar diametrini o‘lchash jarayoni ko‘rsatilgan.
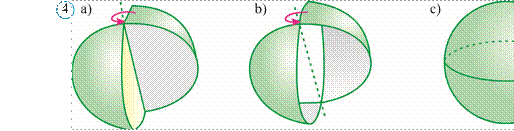
Silindr va konus kabi shar va sfera ham aylanish jismlaridir. Ular mos ravishda, yarim doira va yarim aylanani diametri atrofida aylantirishdan hosil qilinadi (4rasm).
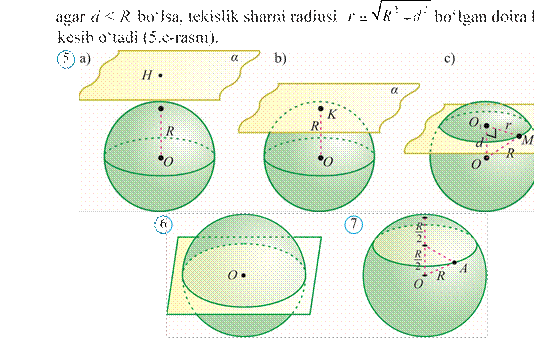
Sharni ixtiyoriy tekislik bilan kesganda kesimda doira hosil bo‘ladi va bu doiraning markazi shar markazidan kesuvchi tekislikka tushirilgan perpendikular asosidan iborat bo‘ladi (5rasm).
Radiusi R ga teng shar markazidan d masofada bo‘lgan tekislik o‘tkazilgan bo‘lsin. Bu holda, agar d > R bo‘lsa, tekislik va shar umumiy nuqtaga ega emas (5.arasm), agar d = R bo‘lsa, tekislik sharga urinadi (5.brasm),
Sharning markazidan o‘tadigan tekislik diametr tekisligi deyiladi. Diametr tekisligining shar bilan kesimi katta doira deyiladi (6rasm), sfera bilan kesimi esa katta aylana deyiladi.
1-masala. Shar radiusining o‘rtasidan unga perpendikular tekislik o‘tkazilgan. Hosil bo‘lgan kesim yuzining katta doira yuziga nisbatini toping.
Yechish. Shartga ko‘ra shar markazidan kesim tekisligigacha bo‘lgan ma
R
sofa d
= ![]() ga teng.
Sharning radiusi R bo‘lsa (7rasm), unda kesimdagi 2
ga teng.
Sharning radiusi R bo‘lsa (7rasm), unda kesimdagi 2
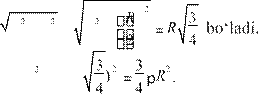 doiraning radiusi r = R −d = R −
doiraning radiusi r = R −d = R −
Kesimning yuzi: S = pr = p(R
3 3
![]()
![]()
![]() Unda kesim yuzin ing
katta doira yuziga nisbati: p p =R R2 : 2
bo‘ladi.
Unda kesim yuzin ing
katta doira yuziga nisbati: p p =R R2 : 2
bo‘ladi.
4 4
Javob: .
 |
Shar sirtidagi S nuqtadan o‘tib, shu nuqtaga o‘tkazilgan radiusga perpendikular bo‘lgan tekislik sharning urinma tekisligi, S nuqtaga esa urinish nuqtasi deyiladi (9rasm).
Ravshanki, urinma tekislik bilan shar faqat bitta umumiy nuqtaga – urinish nuqtasiga ega bo‘ladi.
 |
Urinma to‘g‘ri chiziq ham shar bilan faqat bitta umumiy nuqtaga – urinish nuqtasiga ega bo‘ladi.
Ikkita sferaning kesishishidan aylana hosil bo‘ladi (11.arasm). Kesishish huqtasi faqat bitta nuqtadan iborat sferalar birbiriga urinadigan sferalar deyiladi (11.brasm).
2-masala. Radiusi R ga teng shar tomoni a ga teng muntazam uchburchakning hamma tomonlariga urinadi (12rasm). Shar markazidan uchburchak tekisligigacha bo‘lgan masofani toping.
Yechish. A, B, C – sharning uchburchak tomonlariga urinish nuqtalari bo‘lsin (12rasm). Sharning O markazida uchburchak tekisligiga OO1 perpendikularni tushiramiz. OA, OB, OC kesmalar uchburchak tomonlariga perpendikular. Uch perpendikular haqidagi teoremaga ko‘ra O1A, O1B, O1C kesmalar ham uchburchakning mos tomonlariga perpendikular.
To‘g‘ri burchakli OO1A, OO1B, OO1C uchburchaklar o‘zaro teng. Unda ular uchun OO1 katet umumiy, gipotenuzalari esa radiusga teng:
O1A = O1B = O1C.
Demak, O1 – berilgan uchburchakka ichki chizilgan aylananing markazi.
![]() a 3
a 3
Bu aylananing radiusiga teng.
6
Pifagor teoremasiga ko‘ra, izlanayotgan masofani topamiz. Bu masofa
quyidagiga teng: OO1= ![]() OA OA− .
Javob:
OA OA− .
Javob: ![]()
3-masala. Radiusi R ga teng ikkita teng shar shunday joylashganki, birining markazi ikkinchisining sirtida yotadi (13rasm). Bu sharlar sirtlari kesishgan chiziq uzunligini toping.
Yechish. Sharlarni markazlaridan o‘tuvchi tekislik bilan kesamiz. (14rasm). Ma’lumki, bu sharlar sirti aylana bo‘ylab kesishadi. Mazkur aylananing radiusi tomonlari R ga teng bo‘lgan teng tomonli OAO1 uchburchakning
![]() R 3 balandligiga teng. Bu balandlik ga
teng.
R 3 balandligiga teng. Bu balandlik ga
teng.
2
![]()
![]() Demak, izlanayotgan
chiziqning uzunligi pR 3 ga teng. Javob: pR 3 .
Demak, izlanayotgan
chiziqning uzunligi pR 3 ga teng. Javob: pR 3 .
Agar ko‘pyoqning hamma uchlari shar sirtida yotsa, ko‘pyoq sharga ichki chizilgan deyiladi (15rasm). Shar esa ko‘pyoqqa tashqi chizilgan deb yuritiladi.
Ma’lum bo‘lishicha, har qanday uchburchakli piramidaga yagona tashqi shar chizish mumkin. Shuningdek, to‘g‘ri prizmaning asosiga tashqi aylana chizish mumkin bo‘lsa, bunday prizmaga tashqi shar chizish mumkin va aksincha.
Agar ko‘pyoqning hamma yoqlari shar sirtiga urinsa, bunday ko‘pyoq sharga tashqi chizilgan deyiladi (16rasm). Shar esa ko‘pyoqqa ichki chizilgan deb yuritiladi.
Ma’lum bo‘lishicha, har qanday uchburchakli piramidaga yagona ichki shar chizish mumkin. Shuningdek, to‘g‘ri prizmaning asosiga ichki aylana chizish mumkin va prizma balandligi shu aylana diametridan iborat bo‘lsa, bunday prizmaga ichki shar chizish mumkin va aksincha.
Quyidagi munosabatlarning ham o‘rinli bo‘lishini mustaqil asoslang.
1. Asosiga ichki chizilgan aylana radiusi r1 ga, asosidagi ikki yoqli burchagi α ga teng bo‘lgan muntazam piramidaga r radiusli shar ichki chizilgan bo‘lsa, r = r1sinα / (1+cosα) tenglik o‘rinli bo‘ladi.
2. Balandligi H ga, yon qirrasi l ga teng bo‘lgan muntazam piramidaga R radiusli shar tashqi chizilgan bo‘lsa, l2 = 2HR tenglik o‘rinli bo‘ladi.
4-masala. Muntazam piramidaga tashqi chizilgan sharning markazi uning o‘qida yotishini isbotlang.
Isbot. Sharning O markazidan piramida asosi tekisligiga OA perpendikular tushiramiz (17rasm). X piramida asosining ixtiyoriy bir uchi bo‘lsin. Pifagor teoremasiga ko‘ra AX 2 = OX 2 – OA2 =R2 – OA2 bo‘ladi.
Shunday qilib, AX kesmaning uzunligi piramida asosining istalgan uchi uchun aynan bir xil. Bu esa A nuqta piramida asosiga tashqi chizilgan aylananing markazi ekanini anglatadi.
 Demak, sharining O markazi
piramidaning o‘qida yotadi.
Demak, sharining O markazi
piramidaning o‘qida yotadi.
Agar silindr asoslarining aylanalari shar sirtida yotsa, silindr sharga ichki chizilgan deyiladi (18rasm), shar esa silindrga tashqi chizilgan deb yuritiladi.
Agar shar sirti silindrning asoslari va yon sirtiga urinsa, shar silindrga ichki chizilgan deyiladi (19rasm), silindr esa sharga tashqi chizilgan deb yuritiladi.
Ma’lum bo‘lishicha, silindrning yasovchisi asos diametriga teng bo‘lsa, unga tashqi shar chizish mumkin. Shuningdek, quyidagi munosabatlarning ham o‘rinli bo‘lishini mustaqil asoslang.
1. Silindrga shar ichki chizilgan bo‘lsa, silindrning o‘q kesimi kvadrat va sharning radiusi silindr asosining radiusiga teng bo‘ladi. Silindrning balandligi H, asosining radiusi R, ichki chizilgan shar radiusi r bo‘lsa, u holda H = 2r; R = r.
2. Diagonali d ga teng bo‘lgan silindrga R radiusli shar tashqi chizilgan bo‘lsa, d = 2 R.
Agar konusning uchi va asos aylanasi shar sirtida yotsa, konus sharga ichki chizilgan deyiladi (20rasm), shar esa silindrga tashqi chizilgan deb yuritiladi.
Agar shar sirti konusning asosi va yon sirtiga urinsa, shar konusga ichki chizilgan deyiladi (21rasm), konus esa sharga tashqi chizilgan deb yuritiladi.
Ma’lum bo‘lishicha, har qanday konusga ichki va tashqi shar chizish mumkin. Shuningdek, quyidagi munosabatlarning ham o‘rinli bo‘lishini mustaqil asoslang.
1. Asosining radiusi R ga, yasovchisi bilan asos tekisligi orasidagi burchagi a ga teng bo‘lgan konusga r1 radiusli shar ichki chizilgan bo‘lsa, u holda r1 = R sinα (1 + cosα).
2. Balandligi H ga, yasovchisi l ga teng bo‘lgan konusga R1 radiusli shar tashqi chizilgan bo‘lsa, u holda l2 = 2 HR1.
3. Asoslarining radiuslari R va r ga, balandligi H ga, yasovchisi l ga teng bo‘lgan kesik konusga r1 radiusli shar ichki chizilgan bo‘lsa, u holda H = 2r1 va l = R + r.
5-masala. Sharga tashqi chizilgan kesik konusning yasovchilari o‘rtalaridan o‘tuvchi tekislik bilan shu kesik konus hosil qilgan kesimning yuzi 4π ga teng. Kesik konusning yasovchisini toping.
Yechish. Kesik konus yasovchilari o‘rtalaridan o‘tuvchi tekislik uni doira bo‘ylab kesadi. Bu doiraning radiusi r ga teng bo‘lsin. Masalaning shartiga ko‘ra πr2 = 4 π. Bu yerdan r = 2 ekanini topamiz.
Kesik konusning o‘q kesimida teng yonli trapetsiya hosil bo‘ladi. Bu trapetsiyaning o‘rta chizig‘ini topamiz: l = 2r = 4.
Kesik konus sharga tashqi chizilgani
uchun trapetsiyaga ichki aylana chizish mumkin. Shu sababli trapetsiyaning yon
tomoni x uning o‘rta chizig‘i l ga teng bo‘ladi: x = l =
4. Javob: 4.![]()
Mavzuga oid masalalar va amaliy topshiriqlar
507. Sfera a) to‘g‘ri chiziq; b) tekislik bilan nechta umumiy nuqtaga ega bo‘lishi mumkin?
508. Sferaning radiusi 13 dm ga teng. Sfera markazidan 5 dm masofada tekislik o‘tkazilgan. Hosil bo‘lgan kesimning yuzini hisoblang.
509. K nuqtadan sferagacha bo‘lgan eng qisqa masofa 6 cm, eng uzoq masofa esa 16 cm. Berilgan sfera bilan chegaralangan shar katta doirasining yuzini hisoblang.
510. Sferaning tenglamasi (x + 1)2 + (y –2)2 + (z –1)2 = 25 ko‘rinishda berilgan bo‘lsa, uning markazi va radiusini toping.
511. Markazi C (5; –2; 7) nuqtada, radiusi R = 2 bo‘lgan sfera tenglamasini yozing.
512. Agar sferaning markazi C (3; –2; 1) nuqtada va K (2; –1; –3) nuqta unga tegishli bo‘lsa, sfera tenglamasini yozing.
513. A (2; –3; 5) va B (4; 1; –3) sfera diametrining uchlari bo‘lsa, sfera tenglamasini yozing.
514. Sharning radiusi 10 dm, uning tekislik bilan kesimining yuzi 64p dm2. Sharning markazidan kesim tekisligigacha bo‘lgan masofani toping.
515. Tekislik radiusi 20 cm bo‘lgan sharga urinadi. A nuqta bu tekislikda yotadi va sharning markazidan 25 cm masofada joylashgan. A nuqtadan urinish nuqtasi B gacha bo‘lgan masofani toping (22rasm).
516. Birlik sharga ichki chizilgan to‘g‘ri burchakli parallelepiped sirtining yuzini toping (23rasm).
517. Birlik sharga tashqi chizilgan kub hajmini toping (24rasm).
518. Sferaga tashqi chizilgan kub hajmi 216 ga teng. Sfera radiusini toping. 519. Shardan tashqaridagi M nuqtadan uning sirtiga MN urinma o‘tkazildi. M nuqtadan sharning sirtigacha bo‘lgan eng qisqa masofa 6 ga, sharning markazigacha bo‘lgan masofa 15 ga teng. MN ning uzunligini toping.
520. Shar katta doirasining yuzi 25π ga teng. Sharning markazidan qanday masofada o‘tkazilgan tekislik shardan doirasining yuzi 9π ga teng bo‘lgan kesim ajratadi?
521. Tomonlari 10, 10 va 12 ga teng bo‘lgan uchburchak shar sirtiga urinadi. Uchburchak tekisligidan shar markazigacha masofa 4 ga teng bo‘lsa, sharning radiusini toping.
522. Radiusi 13 ga teng bo‘lgan shar sirtiga diagonallari 30 va 40 ga teng bo‘lgan romb tomonlari urinadi. Romb tekisligidan shar markazigacha bo‘lgan masofani aniqlang.
523. Shar radiusi 6 ga teng. Radius uchidan 30° burchak tashkil qiluvchi tekislik o‘tkazilgan. Shar bilan tekislik hosil qilgan kesimning yuzini toping.
524. Radiusi 15 ga va 20 ga teng bo‘lgan ikki shar markazlari orasidagi masofa 25 ga teng. Shar sirtlari kesishishidan hosil bo‘lgan aylananing uzunligini toping.
525.
![]() Sharning
radiusi 8 π
ga teng. Radiusning oxiridan u bilan 60° li burchak tashkil etadigan kesuvchi
tekislik o‘tkazilgan. Kesimning yuzini toping.
Sharning
radiusi 8 π
ga teng. Radiusning oxiridan u bilan 60° li burchak tashkil etadigan kesuvchi
tekislik o‘tkazilgan. Kesimning yuzini toping.
526. Tomoni 12,5 ga teng bo‘lgan romb tomonlari shar sirtiga urinadi. Sharning radiusi 10 ga teng. Romb tekisligi va shar markazi orasidagi masofa 8 ga teng bo‘lsa, rombning yuzini toping.
527. Ikki kesik konusga ichki chizilgan shar radiuslarining nisbati 2 ga teng.
Bu kesik konuslar balandliklarining nisbatini toping.
528. Asoslarning radiuslari R va r bo‘lgan kesik konusga shar ichki chizilgan. Kesik konus yasovchisining uzunligini toping.
529. Sferaning radiusi 60% uzaytirilsa, sfera o‘q kesimining yuzi necha foiz ko‘payadi?
530. To‘la sirtining yuzi 72 ga teng bo‘lgan kubga tashqi chizilgan sharning radiusini toping.
531. Qirrasining uzunligi 8 ga teng bo‘lgan kubning barcha uchlaridan o‘tuvchi sferaning radiusini toping.
532. Muntazam tetraedrning qirrasi 1 ga teng. Shu tetraedrga tashqi chizilgan sharning radiusini toping.
533. To‘rtburchakli muntazam piramida asosining tomoni 12 ga, unga ichki chizilgan sharning radiusi 3 ga teng. Piramidaning yon sirtini toping.
534. Piramidaning hajmi 25 ga, unga ichki chizilgan sharning radiusi 1,5 ga teng. Piramidaning to‘la sirtini toping.
535. Sharga ichki chizilgan konusning balandligi 3 ga, asosining radiusi
![]() 3 3 ga teng. Sharning
radiusini toping.
3 3 ga teng. Sharning
radiusini toping.
536. Radiusi 5 ga teng bo‘lgan sharga ichki chizilgan konusning balandligi 4 ga teng. Konusning hajmini toping.
537. Sferaga balandligi asosining diemetriga teng bo‘lgan konus ichki chizilgan. Agar sferaning radiusi 2 ga teng bo‘lsa, konus asosining yuzini toping.
Abu Rayhon Beruniy “Astronomiya san’atidan boshlang‘ich ma’lumot beruvchi kitob” nomli asarining geometriyaga tegishli qismida fazoviy jismlar, jumladan, aylanish jismlari haqida qator ma’lumotlar keltirgan.
To‘g‘ri va og‘ma silindrlarga ta’rif bergan. Konusni (asos deb ataluvchi) doiradan yoki boshqa shakldan boshlanib, nuqtada tugovchi jism sifatida tasvirlaydi. Shuningdek, konus uchun silindr mavjudligi va uning bir asosi konusning asosi, ikkinchi asosining markazi esa to‘g‘ri konusning uchi bo‘lishini aytadi. Bu silindrning to‘g‘ri yoki og‘ma bo‘lishiga qarab, konusning ham to‘g‘ri yoki og‘ma bo‘lishini ta’kidlaydi. Beruniyning “Konus hamma vaqt silindrning uchdan birini tashkil qiladi” – degan tasdig‘idan konusning hajmi asosi va balandligi konusning asosi va balandligi bilan bir xil bo‘lgan silindr hajmining uchdan biriga teng, degan jumla kelib chiqadi.
Beruniy konusni tekislik bilan kesganda, kesim: uchburchak, doira, parabola, ellips, giperbola bo‘lishini aytadi va ular haqida batafsil izoh beradi. Beruniy parabolani – “kifoyali kesim”, ellipsni – “yetishmovchi kesim” va giperbolani “ortiqcha kesim” deb nomlaydi.
Shuningdek, Beruniy shar va sferaga ham ta’rif berib ularning qator xossalarini o‘rgangan. Xususan, u doira o‘zining qo‘zg‘olmas diametri atrofida aylantirilsa, shar hosil bo‘lishini ta’kidlab o‘tgan. Sharga ichki chizilgan beshta jism – beshta muntazam ko‘pyoq: kub, ikosaedr, oktaedr, tetraedr va dodekaedrlar haqida ma’lumot bergan. Sharni tekislik bilan kesganda hosil bo‘ladigan kesimlar haqida batafsil ma’lumotlarni keltirgan. Jumladan, kesimda hosil bo‘ladigan katta doira yuzi shar sirti yuzining to‘rtdan biriga tengligi, xuddi shu singari, agar sharning diametri katta doira aylanasining yuziga ko‘paytirilsa, shar sirtining yuzi hosil bo‘lishini aytib o‘tadi. Bu xossalar qadimgi yunon olimi Arximedning “Shar va silindr haqida” degan asarida ham uchraydi. Demak, Beruniy Arximedning shu asari bilan tanish bo‘lgan.
Fazoda berilgan F1 va F2 jismlarni bitta tekislikka parallel tekisliklar bilan kesganda kesimda teng yuzaga ega bo‘lgan shakllar hosil bo‘lsa, bu jismlar hajmi teng bo‘ladi (25 rasm).
Bu ajoyib xossa Kavalyeri prinsipi deb yuritiladi. Uni asoslash uchun F1 va F2 jismlarni bitta tekislikka parallel tekisliklar bilan kesganda hosil bo‘ladigan yupqa qatlamlardan tuzilgan deb olamiz. Bu qatlamlarni bir xil qalinlikdagi (balandlikdagi) to‘g‘ri silindrlar deb olsak, shartga ko‘ra ularning asoslari yuzalari tengligidan bu silindrlarning hajmlari ham birbiriga teng bo‘lishi kelib chiqadi. Unda bu qatlamlardan tuzilgan F1 va F2 jismlarning hajmlari ham o‘zaro teng bo‘ladi (26 rasm).
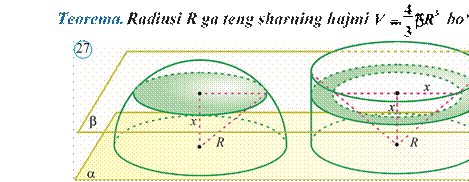
Isbot. a tekislikda yotgan R radiusli yarimshar berilgan bo‘lsin (27rasm). Uning yonida asosi shu tekislikda yotgan, radiusi R ga teng doiradan iborat va balandligi R ga teng bo‘lgan silindrni qaraymiz. Bu silindrga, asosi silindr ning yuqori asosidan iborat, uchi esa silindr pastki asosi markazida bo‘lgan konusni ichki chizamiz.
Berilgan yarimshar hajmi silindrning konusdan tashqari qismi hajmiga teng ekanligini ko‘rsatamiz. α tekislikdan x (0 ≤ x ≤ R) masofada o‘tuvchi va unga parallel β tekislikni o‘tkazamiz. Bu tekislikning yarimshar bilan kesi
![]() mida radiusi R2 − x2
ga, yuzi esa p −(R2 x2) ga teng bo‘lgan doirani
hosil qilamiz.
mida radiusi R2 − x2
ga, yuzi esa p −(R2 x2) ga teng bo‘lgan doirani
hosil qilamiz.
Bu tekislikning ikkinchi jism bilan kesimida tashqi radiusi R ga, ichki radiusi esa x ga teng bo‘lgan halqa hosil bo‘ladi. Bu halqaning yuzi ham p −p =p −R2 x2 (R2 x2) bo‘ladi. Unda Kavalyeri prinsipiga ko‘ra yarimdoira va yasalgan jism hajmlari o‘zaro teng bo‘ladi. Bu hajmni topaylik:
1 2 1 2 2 3 .
V V= silindr −Vkonus =pRR− ![]() pRR=
pRR= ![]() pR
pR
3 3
![]() Sharning hajmi
yarimshar hajmidan ikki marta katta, demak, u V=pR3 bo‘ladi.
Sharning hajmi
yarimshar hajmidan ikki marta katta, demak, u V=pR3 bo‘ladi. ![]()
Shar halqasi deb umumiy markazga ega bo‘lgan ikkita shar sirtlari orasidagi jismga aytiladi (28rasm). Bu sharlar radiuslari, mos ravishda, R va r bo‘lsa (R<r),
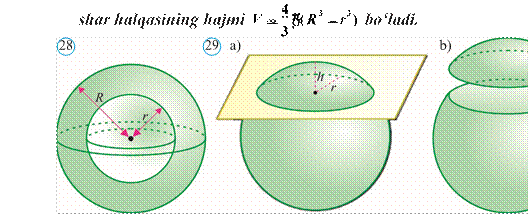
Shar segmenti deb uning markazidan o‘tmaydigan tekislik bilan uni kesganda hosil bo‘lgan shar bo‘laklariga aytiladi (29 rasm). Bu tekislik bilan sharni kesganda kesimda hosil bo‘lgan doira shar segmentining asosi deb ataladi. Shar segmenti asosiga perpendikular shar radiusining segment ichidagi bo‘lagi shar segmentining balandligi deb ataladi.
1 2
![]() Teorema. Shar segmentining hajmi V
Teorema. Shar segmentining hajmi V = ph R h(3 − ) bo‘ladi, bu yerda
3
R – shar radiusi, h esa shar segmentining balandligi.
Isbot. Yana 27rasmga murojaat qilamiz. β tekislik yarimshardan H balandlikka ega bo‘lgan segment ajratgan bo‘lsin, deb faraz qilamiz. Unda bu tekislik silindrdan va unga ichki chizilgan konusdan balandligi h ga teng bo‘lgan silindr va kesik konusni ajratadi.
Unda Kavalyeri prinsipiga ko‘ra, shar segmenti V hajmi silindr va kesik konuslar hajmlarining ayirmasiga teng bo‘ladi.
Silindrning hajmi Vsilindr =pR h2 . Kesik konusning hajmi esa
1
![]()
 3 1 3 2 23
3 1 3 2 23
Vkesik konus = ![]() pR −
pR − ![]() p(R − h) = pR h − pR h + ph .
p(R − h) = pR h − pR h + ph .
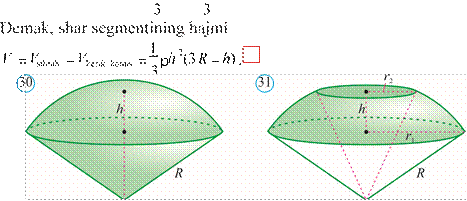
Shar sektori deb shar segmenti va uchi shar markazida, asosi esa shar segmenti asosidan iborat konusdan tashkil topgan shar bo‘lagiga aytiladi (30rasm).
Shar sektorining hajmini shar segmenti va mos konus hajmlarini qo‘shib topish mumkin (30rasm).
2 2
![]() Shar sektorining hajmi V
Shar sektorining hajmi V = pRh bo‘ladi.
3
Shar kamari deb sharning ikki parallel kesuvchi tekisliklar orasidagi bo‘lagiga aytiladi (31rasm). Sharning bu tekisliklar bilan hosil qilgan kesimlari shar kamarining asoslari, bu tekisliklar orasidagi masofa esa shar kamarining balandligi deb aytiladi.
Shar kamarining hajmini shar hajmidan ortiqcha segmentlar hajmlarini ayirib topish mumkin (31rasm). Shar kamari asoslarining radiuslari r1 va r2, balandligi esa h bo‘lsa,
![]()
![]() 1 2 22 shar
kamarining hajmi V
1 2 22 shar
kamarining hajmi V = ph(3r1 − 3r2 + h ) bo‘ladi.
6
Eslatma: Shar va sfera kabi shar segmenti, shar sektori va shar kamarlari ham aylanish jismlaridir. Ular, mos ravishda, quyidagi yassi shakllarning muayyan o‘q atrofida aylantirishdan hosil qilinadi (32rasm):
Mavzuga oid masalalar va amaliy topshiriqlar
538. Diametri 2 marta kattalashtirilgan shar hajmi necha marta kattalashadi? 539. 33rasmda tasvirlangan jismlar hajmini toping.
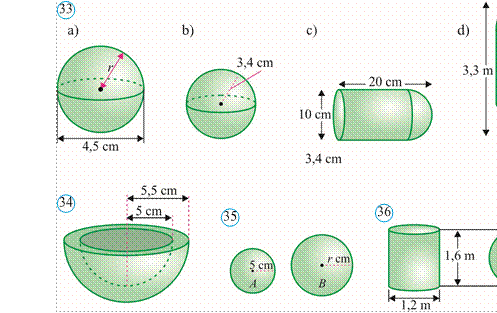
540. Ichki radiusi 5 cm, tashqi radiusi 7 cm bo‘lgan shar halqasining hajmini toping.
541. 34rasmda tasvirlangan qozonning hajmini toping.
542. 35rasmdagi B sharning hajmi A sharning hajmidan ikki marta katta bo‘lsa, uning radiusini toping.
543. 36rasmda berilganlarga ko‘ra, shar va silindrning hajmini toping.
544. Hajmi 8 m3 ga teng bo‘lgan kubga ichki chizilgan shar hajmini toping.
![]() 4 3 ga teng bo‘lgan sharga
ichki chizilgan silindrning o‘q
4 3 ga teng bo‘lgan sharga
ichki chizilgan silindrning o‘q
545. Hajmi p cm 3
kesimining yuzini toping.
546. Radiusi 5 cm va balandligi 3 cm bo‘lgan shar segmenti hajmini toping.
547. Radiusi 3 cm va balandligi 1 cm bo‘lgan shar sektorining hajmini toping.
548. Qirrasi a ga teng bo‘lgan kub berilgan. Kubga a) ichki; b) tashqi chizilgan shar hajmini toping.
549. 37rasmda tasvirlangan yarimdoiraning vertikal diametri atrofida aylanishidan hosil bo‘lgan fazoviy jismning hajmini toping.
 1
1
bo‘lsa, uning radiusini toping. 3
551*. Tegishli o‘lchash ishlarini bajarib, 38rasmda tasvirlangan apelsinning mag‘zi va po‘chog‘ining hajmlari o‘zaro teng ekanligini tekshiring.
552*. Silindrik shakldagi qutiga radiusi 5 cm bo‘lgan uchta tennis koptogi joylashadi (39rasm). Qutining hajmini toping.
553. Radiuslari 2 cm va 5 cm bo‘lgan sovun pufaklari qo‘shilishidan hosil bo‘lgan katta pufakning hajmi qancha bo‘ladi?
554. Radiusi 3 cm va 5 cm bo‘lgan sharlar tarozining bir pallasiga, radiusi 8 cm bo‘lgan shar ikkinchi pallasiga qo‘yildi? Qaysi palla og‘irroq bo‘ladi?
555. Sharning markazidan 6 cm masofada joylashgan kesimning yuzi 64p cm2 bo‘lsa, sharning hajmini toping.
556. Qirrasi 1 m bo‘lgan kubga tashqi chizilgan sharning radiusini toping.
557*. Sharga ichki chizilgan kubning hajmi shar hajmidan necha marta ki chik?
558. Radiusi 2 ga teng bo‘lgan shardan deametri bo‘ylab silindrik teshik teshilgan. Agar silindrik teshikning radiusi 1 ga teng bo‘lsa, sharning qolgan bo‘lagining hajmini hisoblang.
559. Agar shar sektori asosining radiusi 60 cm ga, sharning radiusi esa 75 cm ga teng bo‘lsa, shar sektorining hajmini toping.
560. Shar kamarining asoslari yuzlari 225p cm2, 264p cm2 va shar radiusi 17 cm bo‘lsa, shar kamarining hajmini toping.
561. Massasi 1 kg bo‘lgan qo‘rg‘oshindan radiusi 0,6 cm ga teng bo‘lgan nechta sharcha quyish mumkin? Qo‘rg‘oshinning zichligi 11,4 kg/dm3 ga teng deb oling.
562. Shar shaklidagi handalaklardan birining diametri ikkinchisinikidan ikki marta katta. Birinchi handalak ikkinchisidan necha marta og‘ir?
563. Ikkita shar hajmlarining nisbati m:n kabi. Ular diametrlarining nisbati nimaga teng bo‘ladi?
564. Shar diametriga perpendikular va uni 6 cm va 12 cm qismlarga bo‘luvchi tekislik o‘tkazilgan. Sharning hosil bo‘lgan qismlari hajmlarini hisoblang.
565. Sharni chegaralovchi sfera tenglamasi x2 + y2 + z2 – 6 x + 4y – 6 z = 3 ko‘rinishda bo‘lsa, shar hajmini hisoblang.
566. Asosining radiusi 1 ga teng bo‘lgan silindrga ichki chizilgan sharning hajmini toping (40rasm).
567. Qirrasi 1 ga teng bo‘lgan kubga ichki chizilgan sharning hajmini toping (41rasm).
568. Asosining radiusi 1 ga, yasovchisi 2 ga teng bo‘lgan konusga ichki chizilgan sharning hajmini toping (42rasm).
569. Asosining radiusi 3 ga, balandligi 8 ga teng bo‘lgan silindrga tashqi chizilgan sharning hajmini toping (43rasm).
570. Uzunliklari 1 ga teng kubning qirralariga urinadigan sharning hajmini toping (44rasm).
571. Qirrasi 1 ga teng bo‘lgan kubga tashqi chizilgan sharning hajmini toping (45rasm).
576. Silindr sharga tashqi chizilgan. Shar hajmi 24 ga teng. Silindrning hajmini toping.
577*. Arximed teoremasini isbotlang: Sharning hajmi unga tashqi chizilgan silindr hajmidan 1,5 marta kichik.
578. O‘quvchi qumni yarimshar shaklidagi va radiusi r ga teng bo‘lgan idish dan, radiusi va balandligi r ga teng bo‘lgan konus shaklidagi idishga solayotib, yarimshar hajmi konus hajmidan ikki marta katta, degan xulosaga keldi. Uning tajribadan kelib chiqqan bu xulosasi nazariy jihatdan to‘g‘rimi?
579. 47rasmda berilganlarga ko‘ra masala tuzing va uni yeching.
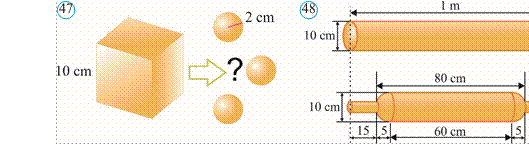
580. 48 rasm asosida masala tuzing va uni yeching.
581. 49rasmda berilganlarga ko‘ra, silindr va shar hajmlari nisbatini toping. 582. 50rasmdagi shar va kub hajmlari teng bo‘lsa, shar radiusini toping.
583. 51rasmdagi shar va konus hajmlari o‘zaro teng bo‘lsa, konusning yasovchisini toping.
584. Radiusi 10 cm bo‘lgan shar kub shaklidagi qutiga zich qilib joylangan.
Qutining bo‘sh qolgan qismining hajmini toping (52rasm).
585. 53rasmdagi jismlar bir xil hajmdagi materialdan yasalgan. Agar sharning radiusi 7 cm, yarimshar diametr kesimi halqasining ichki radiusi 10 cm bo‘lsa, tashqi radiusini toping.
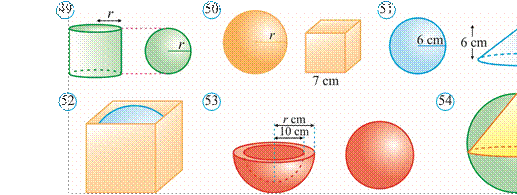
586. Balandligi diametriga teng bo‘lgan silindr shaklidagi taxtadan eng katta hajmli shar yo‘nib olingan. Taxtaning necha foizi chiqitga chiqib ketgan?
587*. Radiusi 10 mm bo‘lgan mis shar bolg‘alanib, qalinligi 3 mm bo‘lgan silindr shaklidagi disk hosil qilingan. Diskning radiusini toping.
588. Konus sharga ichki chizilgan. Konus asosining radiusi shar radiusiga teng. Shar hajmi 28 ga teng. Konusning hajmini toping (54rasm).
589. Konus sharga ichki chizilgan. Konus asosining radiusi shar radiusiga teng. Konusning hajmi 6 ga teng bo‘lsa, sharning hajmini toping.
590.
![]() Kubga
radiusi 3 ga
teng bo‘lgan shar ichki chizilgan. Kubning hajmini toping.
Kubga
radiusi 3 ga
teng bo‘lgan shar ichki chizilgan. Kubning hajmini toping.
591*. Radiusi va balandligi bir xil bo‘lgan silindr, shar va konus shaklidagi idishlar berilgan (55rasm). Silindr idish suvga to‘ldirilib, undagi suv bilan avvaliga konus shaklidagi idish to‘ldirilgan, so‘ng ortib qolgan suv shar shaklidagi idishga quyilgan. Natijada silindr shaklidagi idishda qancha suv qoladi?
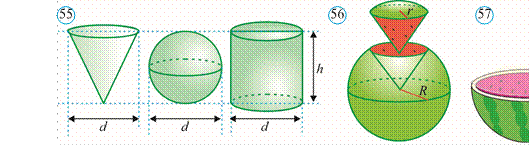
592*. Shar shaklidagi tarvuzdan shar sektori shaklidagi bo‘lagi kesib olingan (56rasm). Rasmdagi berilganlardan foydalanib, butun tarvuz hajmining bo‘lagi hajmiga nisbatini toping.
593. Shar shaklidagi brinchi tarvuzning diametri ikkinchisinikidan 2 marta uzun. Birinchi tarvuz ikkinchisidan necha marta og‘irroq?
594. Radiusi 20 cm bo‘lgan shar shaklidagi tarvuz po‘chog‘ining qalinligi 2 cm. Yarimta tarvuzning qanchasi po‘choqqa chiqib ketadi (57rasm)?
595*. Kub shaklidagi uchta bir xil akvariumga 58rasmda ko‘rsatilgandek, kub yoqlariga yoki (va) birbiriga urinadigan qilib sharchalar joylashtirilgan hamda akvariumlar suv bilan to‘ldirilgan. Akvariumlarning qaysi biriga ko‘proq suv ketadi?
596*. Do‘konda radiusi va balandligi bir xil bo‘lgan silindr, shar va konus shaklidagi shokolad konfetalari sotilmoqda (59rasm). Agar ularning narxi bir xil bo‘lsa, siz ulardan qaysi birini sotib olgan bo‘lar edingiz?
Nega?
597. 60rasmda tasvirlangan beton plitaning o‘lchamlariga ko‘ra uning massasini hisoblang. Bu yerda, o‘yilgan silindr shaklidagi teshiklar diametri d = 10 cm, a= 1,5 m, b = 6 m, n = 20 cm va plita zichligini r = 4 g/cm3 deb oling.
598. 61rasmda tasvirlangan 6 m uzunlikdagi beton plita ko‘ndalang kesimining millimetrlarda berilgan o‘lchamlariga ko‘ra massasini hisoblang (plitaning zichligini r = 4 g/cm3 deb oling).
599. 62rasmda tasvirlangan detallar zichligi 10 g/cm3 bo‘lgan metall dan ishlangan. Qirqish va ishlov berish natijasida metallning 1,5% chiqitga chiqishi ma’lum. Bu detallarning millimetrlarda berilgan o‘lchamlariga ko‘ra, ularni tayyorlashga sarflanadigan metall massasini toping.
600. 63rasmdagi ma’lumotlar asosida berilgan fazoviy jismlar hajmini toping.
601. Yer ekvatorning uzunligi 40 000 km ga, yadrosining radiusi esa 3500 km (64rasm). Yer yadrosining hajmi Yerning hajmidan necha marta kichik?
602*. Radiusi 6 cm bo‘lgan sharcha suvda suzib yuribdi (65rasm). Agar sharcha materialining zichligi 0,7 g/cm3 bo‘lsa, sharchaning suvdan chiqib turgan qismining balandligini toping.
603*. Kosmik kema Yerga tushadigan apparatining radiusi 1 m bo‘lgan shar shaklida (66rasm). Suvga tushganda cho‘kib ketmasligi uchun bu apparatning massasi qancha bo‘lishi kerak?
604. Plasmassadan ishlangan sharchaning diametri 0,6 cm. Agar plasmassa zichligi 0,15 g/cm3 ekanligi ma’lum bo‘lsa, sharchalardan nechtasining massasi 8 kg bo‘ladi?
605. Bolalar to‘pining diametr kesimi 67rasmda berilgan. Rasmda berilgan ma’lumotlardan foydalanib, bu to‘pni ishlab chiqarish uchun sarflangan rezina hajmini toping.
606*. Bozorda bir xil radiusli ikki xil navli tarvuz sotilmoqda (68 rasm). Birinchisining po‘chog‘i yupqa bo‘lib, u 5000 so‘mdan, ikkinchisi radiusining 20 foizi po‘choqdan iborat bo‘lib, u 3500 so‘mdan sotilmoqda.
Qaysi tarvuzni sotib olgan bo‘lar edingiz?
607. Yer ekvatori lenta bilan tarang qilib o‘raldi. So‘ng lentaning uzunligi 1 m ga uzaytirildi (69rasm). Bu lenta tagidan mushuk o‘ta oladimi?
608. Mis halqa qizdirilganda uning teshigi kengligi 1,5 marta uzaydi. Halqa teshigining yuzi qanchaga o‘zgardi?
609*. Globus ekvatorining uzunligi 1 m ga teng. Yetishmayotgan ma’lumotlarni qidirib topib, Yer hajmining globus hajmiga nisbatini toping.
610. Jism bir yo‘nalishda k marta cho‘zilsa, uning hajmi qanday o‘zgaradi?
611. Filning barcha chiziqli o‘lchamlari ikki marta uzaytirilsa, uning massasi qanchaga o‘zgaradi (70.arasm)? Fil rasmining yuzichi (70.b rasm)?
612*. Kovak shar devorining hajmi 252p cm3 ga, devorning qalinligi 3 cm ga teng. Tashqi sharning radiusini toping.
Sferaga yoqlari kichik qavariq ko‘pburchaklardan iborat ko‘pyoqni tashqi qilib chiqamiz (71.arasm). Bu ko‘pyoq sirtining yuzi, ya’ni barcha qavariq ko‘pburchaklar yuzlarining yig‘indisi S' ga teng bo‘lsin. Ko‘pyoq yoqlarining chiziqli o‘lchovlari, ya’ni istalgan ikki nuqtasi orasidagi masofa ε dan kichik deb faraz qilamiz va ko‘pyoq sirti yuzining taqribiy qiymatini topamiz.
Ko‘pyoqning hajmi asosi ko‘pyoqning
yoqlaridan iborat, uchi esa sferaning O markazida bo‘lgan piramidalar
hajmlarining yig‘indisiga teng (71.brasm). Har bir piramidaning OA balandligi
sferaning R radiusiga teng (71.crasm). Shuning uchun ko‘pyoqning hajmi V = ![]() SʹR bo‘ladi.
SʹR bo‘ladi.
Ko‘pyoqning hajmi sfera bilan chegaralangan sharning hajmidan katta, biroq o‘sha markazli va R + ε radiusli sharning hajmidan kichik bo‘ladi. Shunday qilib,
4 3 1 4 3 ![]() pR <
pR < ![]() S R'' <
S R'' < ![]() p(R + ε) .
p(R + ε) .
3 3 3
Bundan 4pR2 < S' < 4 (p R + ε)21+ ![]() ε
ga ega bo‘lamiz.
ε
ga ega bo‘lamiz.
R
Tashqi chizilgan ko‘pyoq yoqlarining o‘lchamlari cheksiz kamaytirilganga, ya’ni ε cheksiz kamayganda, ko‘pyoq sirti 4 πR2 ga yaqinlashadi. Shuning uchun 4 π R2 soni sferaning yuzi sifatida qabul qilinadi.
Shunday qilib, R radiusli sferaning yuzi
S = 4 π R2
formula bo‘yicha hisoblanadi, ya’ni u to‘rtta katta doira yuziga teng.
Yuqoridagi mulohazalardan quyidagi natijalar kelib chiqadi:
1. Shar sektori sirti sferik qismining (72rasm) yuzi, ya’ni sferik segmentning yuzi S = 2πRh, bu yerda R – shar radiusi, h – segmentning balandligi.
2. R
radiusli sharga tashqi chizilgan ko‘pyoqning hajmi V = ![]() SR , bu yerda
S ko‘pyoq to‘la sirtining yuzi (73 rasm).
SR , bu yerda
S ko‘pyoq to‘la sirtining yuzi (73 rasm).
3. R
radiusli sharning hajmi V = ![]() SR , bu yerda
S shar sirtining yuzi.
SR , bu yerda
S shar sirtining yuzi.
Mavzuga oid masalalar va amaliy topshiriqlar
613. Sharning katta doirasi yuzi 3 ga teng. Shar sirtining yuzini toping.
614. Radiusi R ga teng bo‘lgan sharning hajmi V, sirtining yuzi S bilan belgilangan. a) agar R = 4 cm bo‘lsa, S va V ni toping; b) agar V = 4000 cm3 bo‘lsa, R va S ni toping; c) agar S = 64π cm2 bo‘lsa, R va V ni toping.
615. Radiusi 10 cm bo‘lgan futbol to‘pini tayyorlash uchun qancha teri materiali kerak bo‘ladi? (To‘pni tayyorlashda 10% material chiqitga chiqishini hisobga oling).
616. Sfera radiusi uch marta kattalashtirilsa, uning sirti yuzi qancha kattalashadi?
617. Shar shaklidagi pufak shishirildi. Bunda uning sirti yuzi 9% ga oshgan bo‘lsa, uning radiusi qanchaga uzaydi?
618. Shar tekislik bilan hajmi 720π cm3 va 252π cm3 bo‘lgan bo‘laklarga bo‘lingan. Shar sirtining yuzini topong.
619. Sferaning tenglamasi a) x2+ y2 + z2 = 3; b) x2+ 2x + y2 + + z2 = 0;
c) (x–1)2+(y+1)2+(z–2)2=16; d) x2 –2x+y2+2y+z2 –4z=3 ko‘rinishda berilgan bo‘lsa, uning yuzini hisoblang.
620. Sferaning tenglamasi x2+ y2 + z2 –4x + 6y + 6z – 3 = 0 ko‘rinishda berilgan bo‘lsa, uning sirti yuzini hisoblang.
621. Yer sirtining taxminan 75 foizini suv tashkil qiladi. Yerning radiusi 6375 km bo‘lsa, Yer yuzasi quruqlik qismining yuzini toping.
622. Balandligi 50 cm va radiusi 3 m bo‘lgan shar segmenti shaklidagi tepalikni hosil qilish uchun necha kub metr tuproq kerak bo‘ladi?
623. Shar shaklidagi radiuslari 10 cm va 20 cm bo‘lgan handalaklardan qaysi birini tanlagan bo‘lar edingiz? Nega?
624*. Oyning diametri Yer diametridan taxminan 4 marta kichik. Oy va Yerning shaklini shar deb olib, ularning hajmlari nisbatini toping.
625*. Mars diametri Yer diametrining yarmini tashkil qiladi. Mars va Yerning shaklini shar deb olib, Mars sirti Yer sirtidan necha marta kichik ekanligini aniqlang.
626*. Quyoshning diametri Oy diametridan 400 matra katta. Quyosh sirtining yuzi Oy sirtining yuzidan necha marta katta?
627. O‘lchamlari 20 cm, 20 cm va 10 cm bo‘lgan to‘g‘ri burchakli parallelepiped shaklidagi mis parchasi eritilib, shar shaklida quyilgan. Sharning radiusini toping.
628. Radiusi 2 cm bo‘lgan sharlarning nechtasidan radiusi 6 cm bo‘lgan shar hosil qilish mumkin?
629. Radiusi 3 cm, 4 cm va 5 cm bo‘lgan mis sharlarni eritib, qanday radiusli sharni hosil qilish mumkin?
630. Olcha danagini qalinligi danak diametriga teng bo‘lgan mag‘zi qoplab turadi. Olcha va uning danagini shar shaklida deb olib, olcha mag‘zi hajmining uning danagi hajmiga nisbatini toping.
631. Radiusi 1 m bo‘lgan shar sirtini qalinligi 0,5 mm bo‘lgan bo‘yoq bilan bo‘yash uchun qancha hajmdagi bo‘yoq kerak bo‘ladi?
632. Sharga silindr ichki chizilgan. Silindrning to‘la sirtining yuzi 18 ga teng. Shar sirtining yuzini toping.
633. Kubning qirrasi a ga teng. a) kubga ichki chizilgan; b) kubga tashqi chizilgan; c) kubning barcha qirralari o‘rtasidan o‘tuvchi sfera sirtining yuzini toping.
634. Tekislik sfera sirtini yuzi 12 dm2 va 24 dm2 bo‘lgan bo‘laklarga ajratgan. Kesimda hosil bo‘lgan doira yuzini toping.
635*. Qirrasi 1,6 ga teng ABCDA1B1C1D1 kubning A uchi A1 nuqtadan o‘tuvchi sferaning markazi hisoblanadi (74rasm). Sferaning kub ishida joylashgan qismi sirtining yuzini toping.
636*. Qirrasi 1,9 ga teng kubning bitta qirrasining o‘rtasi – radiusi 0,95 ga teng bo‘lgan sharning markazidir (75rasm). Sharning kub ichida joylashgan qismi sirtining yuzini toping.
637. Ikkita shar berilgan. Birinchi shar radiusi ikkinchi shar radiusidan 2 marta katta. Birinchi shar sirtining yuzi ikkinchisinikidan qancha marta katta?
638. Shar radiusi uch marta kattalashtirilsa, uning hajmi qancha kattalashadi?
639. Uchta shar radiuslari, mos ravishda, 6, 8, 10 ga teng. Hajmi shu uchta shar hajmiga teng bo‘lgan shar radiusini toping.
640. Birinchi shar hajmi ikkinchisinikidan 27 marta katta. Birinchi shar sirtining yuzi ikkinchisinikidan necha marta katta?
641. Ikkita shar radiuslari, mos ravishda, 6 va 8 ga teng. Hajmi shu ikkita shar hajmiga teng bo‘lgan shar radiusini toping.
642*. Shar sektori sirti sferik qismining yuzi, ya’ni sferik segment yuzi S = 2πRh ga teng ekanligini asoslang, bu yerda R – shar radiusi, h – segmentning balandligi.
643*. R
radiusli sharga tashqi chizilgan ko‘pyoqning hajmi V = ![]() SR ga teng
ekanligini asoslang, bu yerda S ko‘pyoq to‘la sirtining yuzi.
SR ga teng
ekanligini asoslang, bu yerda S ko‘pyoq to‘la sirtining yuzi.
644*. R
radiusli sharning hajmi V = ![]() SR ekanligini
asoslang, bu yerda S shar sirtining yuzi.
SR ekanligini
asoslang, bu yerda S shar sirtining yuzi.
645*. 76rasmda osmon jismlarini kuzatish uchun mo‘ljallangan observatoriya binosi keltirilgan. Rasmda berilganlardan foydalanib, observatoriya devorlari va tomining sirtini toping. Arag 1 gallon bo‘yoq 300 kvadrat fut sirtni bo‘yashga yetishi ma’lum bo‘lsa, observatoriya sirtini bo‘yash uchun necha gallon bo‘yoq kerak bo‘ladi?
646. 77rasmda berilgan ma’lumotlar asosida berilgan fazoviy jismning to‘la sirti va hajmini toping.
647. 78rasmda tasvirlangan fazoviy jismlarning balandliklari teng. Qaysi jismning to‘la sirti katta?
648. Sferani bo‘yash uchun 250 g bo‘yoq kerak bo‘ldi (79rasm). Qirrasi sfera radiusiga teng bo‘lgan kubni bo‘yash uchun qancha bo‘yoq kerak bo‘ladi?
649*. Apelsin 8 ta teng bo‘lakka bo‘lindi (80rasm). Barcha bo‘laklarning to‘la sirti apelsin to‘la sirtidan qanchaga katta?
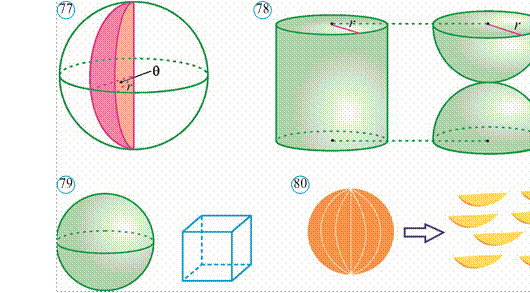
650. Shar shaklidagi shokolad eritilib, undan kub shaklidagi shokolad yasaldi (81rasm). Qaysi shaklning to‘la sirti kichikroq bo‘ladi?
651*. 1060 km balandlikda uchib borayotgan fazoviy kemadagi fazogir Yerning qanday qismi sirtini kuzatish imkoniyatiga ega? 40 paralleldan shimolda joylashgan Yer sirtining yuzini toping. Masalani yechishda Yer radiusini 6 370 km deb oling va 82rasmdan foydalaning.
652*. Globus ekvatorining uzunligi 1 m ga teng. Yetishmayotgan ma’lumotlarni qidirib topib, globusda O‘zbekiston egallagan maydon yuzini toping.
Quyosh sistemasidagi sayyoralarning harakat qonunini kashf qilgan nemis astronomi Iogann Kepler ( 1571–1630) muntazam ko‘pyoqlar bilan qiziqib qolib, 1596yilda bu xususida o‘z qarashlarini “Dunyo yaralishining siri” deb nomlangan asarida bayon etdi. Mavjud sayyoralar harakat orbitalari (harakatlanish trayektoriyalari) orasidagi masofalarni birbiriga ichmaich joylashgan Platon jismlaridan foydalanib topish mumkinligini ko‘rsatib berdi.
Keplerning sayyoralar geometriyasi quyidagicha edi (83 rasm). “Yer (Yer orbitasi) hamma orbitalar uchun o‘lchov birligi hisoblanadi. Uni shar deb olib unga dodekaedrni tashqi chizamiz. Dodekaedrga tashqi chizilgan sfera Mars orbitasidir. Mars orbitasi sferasiga tetraedrni tashqi chizamiz. Tetraedrga tashqi chizilgan sfera Yupiter orbitasidan iborat bo‘ladi. Yupiter orbitasi sferasiga kubni tashqi chizamiz. Kubga tashqi chizilgan sfera Saturn orbitasini tashkil qiladi. Yer orbitasi sferasiga ikosaedrni ichki chizamiz. Unga ichki chizilgan sfera Venera orbitasidan iborat bo‘ladi. Venera sferasiga oktaedrni ichki chizamiz. Oktaedrga ichki chizilgan sfera Merkuriy sayyarasi orbitasidan iborat bo‘ladi.
Kepler shu tariqa muntazam ko‘pyoqlardan foydalanib, o‘zining “Koinot kubogini” qurdi.Bu hisoblar haqiqatdan ham sayyoralar orbitalari orasidagi masofalarga juda yaqin bo‘lgan.
4TEST TOPSHIRIG‘I
1. Agar sferaning radiusi 50% orttirilsa, sfera sirtining yuzi necha foizga ko‘payadi?
A) 125%; B) 100%; C) 150%; D) 75%.
2. Radiusi 13 ga teng bo‘lgan shar tekislik bilan kesilgan. Agar shar markazidan kesimgacha masofa 10 ga teng bo‘lsa, kesimning yuzini toping.
A) ![]() 69π; B)
3 6p; C) 100π; D)
3.
69π; B)
3 6p; C) 100π; D)
3.
3. Shar sirtining yuzi Q bo‘lsa, uning hajmi nimaga teng?
![]()
![]()
![]() A) Q Q / 6 ;
B)
A) Q Q / 6 ;
B) ![]() 3 Qπ; C)
4 Q ; D) 3 Q Q .
3 Qπ; C)
4 Q ; D) 3 Q Q .
4. Sharni bo‘yash uchun 100 gramm bo‘yoq ishlatildi. Agar sharning diametri uch marta orttirilsa, uni bo‘yash uchun necha gramm bo‘yoq kerak bo‘ladi? A) 900; B) 300; C) 600; D) 450.
5. Radiusi 5 ga teng bo‘lgan shar markazidan 3 ga teng bo‘lgan masofada tekislik bilan ikkita jismga ajratildi. Shu jismlardan kichigining hajmini toping.
A) 17![]() π; B) 15
π; B) 15![]() π; C) 17
π; C) 17![]() π; D) 16
π; D) 16![]() π.
π.
6. Radiusi 2 ga teng bo‘lgan yarimshar balandligining o‘rtasidan yarimsharning asosiga parallel tekislik o‘tkazilgan. Hosil bo‘lgan shar qatlamining hajmini toping.
A) 10π/3; B) 11π/3; C) 4π; D) 3π.
7. Sfera sirtidagi uchta nuqta orasidagi masofa 26, 24 va 10 ga, sfera sirtining yuzi esa 900π ga teng. Shu uchta nuqta orqali o‘tgan tekislikdan sferaning markazigacha bo‘lgan masofani toping.
A) ![]()
![]()
![]() 2π 14 ; B)
2 14 ; C)
4 14 ;
D) 56π.
2π 14 ; B)
2 14 ; C)
4 14 ;
D) 56π.
8. Hajmi 125 bo‘lgan kubga ichki chizilgan shar sirtining yuzini toping. A) 125π; B) 25π; C) 24,5π; D) 105π.
9.
![]() Ikkita
qo‘shni yoqlarining markazlari orasidagi masofa 2 2 ga teng bo‘lgan kubga tashqi chizilgan
shar sirtining yuzini toping.
Ikkita
qo‘shni yoqlarining markazlari orasidagi masofa 2 2 ga teng bo‘lgan kubga tashqi chizilgan
shar sirtining yuzini toping.
A) ![]() 28π; B)
36π; C) 48π; D) 18 2 π.
28π; B)
36π; C) 48π; D) 18 2 π.
10. Radiusi
![]() ga
teng yarimsharga kub ichki chizilgan bo‘lib, uning to‘rtta uchi yarimshar
asosida, qolgan to‘rttasi shar sirtida yotadi. Kubning hajmini toping.
ga
teng yarimsharga kub ichki chizilgan bo‘lib, uning to‘rtta uchi yarimshar
asosida, qolgan to‘rttasi shar sirtida yotadi. Kubning hajmini toping.
3 3
A) ![]() 1; B) ; C)
2,25; D) 2.
1; B) ; C)
2,25; D) 2.
2 2
11. Kubga tashqi chizilgan sharning hajmi 1023π ga teng. Kubning diagonaliga tegishli bo‘lmagan uchlaridan diagonalgacha bo‘lgan masofani toping.
A) ![]()
![]()
![]() 4 2 /3; B) 3 2 /4; C) 4 2 /9; D)3
3 /8.
4 2 /3; B) 3 2 /4; C) 4 2 /9; D)3
3 /8.
12. ![]() Kubning bir uchidan chiqqan
uchta qirralarining o‘rtalari orqali o‘tkazilgan kesimning yuzi 16 3 ga teng. Shu
kubga ichki chizilgan shar sirtining yuzini hisoblang.
Kubning bir uchidan chiqqan
uchta qirralarining o‘rtalari orqali o‘tkazilgan kesimning yuzi 16 3 ga teng. Shu
kubga ichki chizilgan shar sirtining yuzini hisoblang.
A) 96π; B) 256π; C) 144π; D) 128π.
1
13. Kubga
ichki chizilgan sharning hajmi 85 ![]() π ga
teng. Shu kubning to‘la
π ga
teng. Shu kubning to‘la
3 sirtini toping.
A) 382; B) 386; C) 385; D) 384.
14. Piramidaning to‘la sirti 60 ga, unga ichki chizilgan sharning radiusi 5 ga teng. Piramidaning hajmini toping.
A) 120; B) 80; C) 90; D) 100.
15. Oltiburchakli muntazam piramidaning apofemasi 5 ga, uning asosiga tash qi chizilgan doiraning yuzi 12 π ga teng. Shu piramidaga ichki chizilgan sharning radiusini toping.
A) 3; B) 3,2; C) 1,5; D) 2,5.
16. Uchburchakli muntazam piramidaga tashqi chizilgan sharning markazi uning balandligini 6 va 3 ga teng bo‘lgan qismlarga ajratadi. Piramidaning hajmini toping.
A) ![]()
![]()
![]()
![]() 25 3 /4; B) 81 3 /2; C)
729 3 /4;
D) 243 3 /4.
25 3 /4; B) 81 3 /2; C)
729 3 /4;
D) 243 3 /4.
17. Kubga ichki chizilgan silindrning hajmi unga ichki chizilgan konusning hajmidan π ga ortiq. Kubning hajmini toping.
A) 4; B) 6; C) 8; D) 12.
18. O‘q kesimi kvadratdan iborat silindrga radiusi 3 ga teng bo‘lgan shar ichki chizilgan. Silindr va shar sirtlari orasidagi jismning hajmini toping.
A) 27π; B) 24π; C) 18π; D)12π.
19. O‘q kesimi kvadratdan iborat silindrga radiusi 2 ga teng bo‘lgan shar tashqi chizilgan. Silindr hajmini toping.
A) ![]()
![]()
![]() 2 2 π; B) 3 2 π; C)
4 2 π;
D)8π.
2 2 π; B) 3 2 π; C)
4 2 π;
D)8π.
20. Silindrga shar ichki chizilgan. Silindrning hajmi 16π ga teng bo‘lsa, sharning hajmini toping.
A)
![]() 32π/3; B) 16π/3; C)
64π/3; D)10 π.
32π/3; B) 16π/3; C)
64π/3; D)10 π.
21. Kesik konusga shar ichki chizilgan. Konus ustki asosining yuzi 36π ga, ostki asosining yuzi esa 64π ga teng. Shar sirtining yuzini toping.
A) 172π; B) 100π; C) 144π; D) 192π.
22. Radiusi 2 ga teng shar konusga ichki chizilgan. Konus yasovchisi va balandligi orasidagi burchak 30° ga teng. Konus yon sirtining yuzini toping.
A) 24π; B) 4π; C) 16π; D) 18π.
23. Balandligi 6 ga, yasovchisi 10 ga teng konusga ichki chizilgan sharning sirtini toping.
A) 32π/3; B) 64π/3; C) 256π/9; D) 64π/9.
24. Radiusi 10 ga teng bo‘lgan sferaga balandligi 18 ga teng bo‘lgan konus ichki chizilgan. Konusning hajmini toping.
A) 210π; B) 216π; C) 220π; D) 228π.
25. Sharga balandligi asosining diametriga teng bo‘lgan konus ichki chizilgan. Agar konus asosining yuzi 2,4 ga teng bo‘lsa, shar sirtining yuzini toping.
A) 9π; B) 6; C) 12,5; D) 15.
26. O‘q kesimi teng tomonli uchburchakdan iborat konusga diametri D ga teng sfera ichki chizilgan. Konusning to‘la sirtini toping.
A) ![]() πD2; B)
πD2; B) ![]() πD2; C)
πD2; C) ![]() πD2; D)
πD2; D) ![]() πD2.
πD2.
27. Sharga konus shunday ichki chizilganki, konusning yasovchisi asosining diametriga teng. Konusning to‘la sirti shar sirti yuzining necha foizini tashkil etadi?
A) 62; B) 56,25; C) 54,5; D) 60,75.
28. Kesik konus asoslarining yuzlari 9π va 25π ga teng. Agar bu konusga sharni ichki chizish mumkin bo‘lsa, konusning yon sirtini toping.
A) 80π; B) 36π; C) 54π; D) 64π.
29. Yasovchisi 5 ga, asosining diametri 6 ga teng bo‘lgan konusga ichki chizilgan shar sirtining yuzini toping.
A) 16π; B) 64π/11; C) 9π; D) 71π/9.
30. Kesik konusga shar ichki chizilgan. Agar kesik konus asoslarining yuzlari π va 4π ga teng bo‘lsa, shu konus yon sirtining yuzini toping.
A) 6π; B) 7π; C) 8π; D) 9π.
Masalalar
652. O – shar markazi, O1 – shar kesimining markazi (84rasm). ∠AOB= 60°, ∠ABO1= 45°. Sharning katta doirasi yuzi 12 ga teng. Kesim yuzini toping.
653. Silindr sferaga tashqi chizilgan (85rasm). Sfera sirtining yuzi 20 ga teng. Silindr to‘la sirtining yuzimi toping.
654. Silindr radiusi 2 ga teng sferaga tashqi chizilgan. Sfera sirtining yuzi 20 ga teng. Silindr hajmini toping.
655. Silindr sharga tashqi chizilgan. Shar hajmi 16 ga teng. Silindr hajmini toping.
656. Radiusi 6 ga teng sharga asos diametri va yasovchisi teng bo‘lgan konus ichki chizilgan (86rasm). Konusning hajmini toping.
657. Radiusi 3 ga teng sharga konus ichki chizilgan. Shar markazi konus asosiga tegishli (87rasm). Konusning hajmini toping.
658. Kubning qirrasi 6 ga teng (88rasm). Kubga ichki chizilgan shar hajmini toping.
659. Radiuslari 2, 3 va 4 ga teng bo‘lgan metall sharlar eritilib, bitta shar quyildi. Shu sharning hajmini toping.
660. Kovak shar devorining hajmi 156π ga, devorning qalinligi 2 ga teng. Tashqi sharning radiusini toping.
661. Hajmi 9π/16 ga teng shar sirtining yuzini aniqlang.
662. ![]() Radiusi 3 2 bo‘lgan shar
sirti, yon sirti asosining yuzidan 3 marta katta bo‘lgan konus sirtiga teng.
Konusning balandligini toping.
Radiusi 3 2 bo‘lgan shar
sirti, yon sirti asosining yuzidan 3 marta katta bo‘lgan konus sirtiga teng.
Konusning balandligini toping.
663. ![]() Kubning diagonali 3 ga teng. Kubga
ichki chizilgan shar hajmini toping.
Kubning diagonali 3 ga teng. Kubga
ichki chizilgan shar hajmini toping.
664. Radiusi 5 ga teng bo‘lgan sharga balandligi 8 ga teng to‘rtburchakli muntazam prizma ichki chizilgan. Prizmaning hajmini toping.
665. Radiusi R ga teng sharga balandligi H ga teng bo‘lgan uchburchakli muntazam prizma ichki chizilgan. Prizmaning hajmini toping.
666. Sakkizburchakli muntazam piramidaning apofemasi 10 ga, uning asosiga ichki chizilgan doiraning yuzi 36π ga teng. Shu piramidaga ichki chizilgan sharning radiusini toping.
667. Oltiburchakli muntazam piramidaning to‘la sirti 2000 ga, hajmi 4800 ga teng. Shu piramidaga ichki chizilgan sharning radiusini toping.
668. To‘rtburchakli muntazam kesik piramida kichik asosining yuzi 50 ga, katta asosining yuzi 200 ga teng. Shu piramidaga ichki chizilgan sfera sirtining yuzini toping.
669*. Radiusi 1 ga teng bo‘lgan sferaga ichki chizilgan eng katta hajmli silindrning balandligini aniqlang.
670*. Radiusi 6 cm bo‘lgan metall shardan eng katta hajmli silindr yo‘nilgan. Bu silindr asosining radiusi nechaga teng?
671. O‘q kesimi kvadratdan iborat silindr shaklidagi g‘o‘ladan eng katta hajmdagi shar yo‘nib olindi. G‘o‘laning qancha foizi chiqitga ketgan?
672. O‘q kesimi teng tomonli uchburchak bo‘lgan konusga shar tashqi chizilgan. Shar sirtining konus to‘la sirtiga nisbatini toping.
673. Sharga konus ichki chizilgan. Konusning yasovchisi asosining diametriga teng. Shar hajmining konus hajmiga nisbatini toping.
674. Sharga tashqi chizilgan kesik konusning yasovchilari o‘rtalaridan o‘tuvchi tekislik bilan shu kesik konus hosil qilingan kesimning yuzi 4π ga teng. Kesik konusning yasovchisinini toping.
675. Kesik konusning yon sirti 10π ga, to‘la sirti 18π ga teng. Konusning to‘la sirti unga ichki chizilgan shar sirtidan qancha ko‘p?
676*. R radiusli yarimsharga asosining markazi bilan ustmaust tushadigan konus tashqi chizilgan. Konusning balandligi qanday bo‘lganda, uning hajmi eng kichik bo‘ladi?
677. Konus asosining yuzi 9π ga, yon sirtining yuzi 15π ga teng. Shu konusga ichki chizilgan sferaning radiusini toping.
678. Teng tomonli konusga ichki va tashqi shar chizildi. Ichki chizilgan shar hajmi tashqi chizilgan shar hajmining necha foizini tashkil etadi?
679*. Radiusi R ga teng bo‘lgan shar ichiga chizilgan eng katta hajmga ega bo‘lgan konusning balandligini toping.
680. ![]() Radiusi 1 ga teng bo‘lgan
sharga yasovchisi 3
ga teng bo‘lgan konus ichki chizildi. Shu konus o‘q kesimining uchidagi
burchakning kattaligini toping.
Radiusi 1 ga teng bo‘lgan
sharga yasovchisi 3
ga teng bo‘lgan konus ichki chizildi. Shu konus o‘q kesimining uchidagi
burchakning kattaligini toping.
681. Silindr va unga tashqi chizilgan muntazam parallelepiped asosining tomoni 4 ga teng. Silindrning hajmini toping.
682. Hajmi 432π ga teng bo‘lgan silindrning o‘q kesimi kvadratdan iborat.
Silindrga ichki chizilgan shar sirtining yuzini toping.
683. Uchburchakli muntazam prizmaga tashqi chizilgan silindr yon sirti yuzining unga ichki chizilgan silindr yon sirti yuziga nisbatini toping.
684. To‘rtburchakli muntazam prizmaga silindr ichki chizilgan. Silindr hajmining prizma hajmiga nisbatini toping.
685. Qirrasi 12 ga teng kubga konus ichki chizilgan. Agar konusning asosi kubning ostki asosiga ichki chizilgan bo‘lsa, uchi esa yuqoridagi asosining markazida yotsa, konusning hajmini toping.
686. Qirrasi 6 ga teng bo‘lgan kubga konus ichki chizilgan. Konusning asosi kubning yuqoridagi asosiga ichki chizilgan, uchi esa kubning quyi asosining markazida. Konusning hajmini toping.
687. To‘rtburchakli muntazam prizmaga konus ichki chizilgan. Konusning asosi prizmaning ostki asosida, uchi esa prizma ustki asosining markazida yotadi. Prizma hajmining konus hajmiga nisbatini toping.
688. Uchburchakli muntazam piramidaga konus ichki chizilgan. Agar piramidaning yon yoqlari bilan asosi 60° li burchak hosil qilib, piramidaning asosiga ichki chizilgan aylananing radiusi 16 ga bo‘lsa, konusning yon sirtini toping.
689. Konus asosining radiusi 2 ga, o‘q kesimining uchidagi burchagi 60° ga teng. Shu konusga tashqi chizilgan uchburchakli muntazam piramidaning hajmini toping.
690. Sfera silindrga ichki chizilgan. Sfera sirtining yuzi 20 ga teng. Silindr yon sirtining yuzi 23 ga teng. Sfera sirtining yuzini toping.
4nazorat ishi namunasi
1. Sharning katta doirasi yuzi 16 ga teng. Shar sirtining yuzini toping.
2. Sharga tashqi chizilgan kubning hajmi 8 ga teng. Sharning radiusini toping.
3. O‘q kesimi kvadratdan iborat silindrga ichki chizilgan sharning hajmi 9π/16 ga teng. Silindrning yon sirtini toping.
4. Sharga ichki chizilgan konusning asosi sharning katta doirasiga teng. Konus o‘q kesimining yuzi 9 ga teng. Sharning hajmini toping.
5. Sharga ichki chizilgan konusning o‘q kesimi teng yonli to‘g‘ri burchakli uchburchakdan iborat. Konus hajmi shar hajmining qanday qismini tashkil etadi?
Mazkur bobda oliy o‘quv yurtlariga kirish imtihonlarida stereometriya kursidan berilgan test topshiriqlari keltirilgan. Ularni yechib, stereometriyani takrorlang va shu bilan birga stereometriya kursidan olgan bilimlaringizni tekshirib ko‘ring.
1.
![]() a (–3; 2; –1) va b (–4; 4;
1) vektorlar berilgan bo‘lsa, ularning yig‘indisini toping.
a (–3; 2; –1) va b (–4; 4;
1) vektorlar berilgan bo‘lsa, ularning yig‘indisini toping.
A) (7; 6; 0); B) (–7; 6; 0); C) (12; 8; –1); D) (–7; 6; –1).
2. a (3x; 2;–1) va b (x; –2x;–1) vektorlar berilgan. x ning qanday qiymatida ular o‘zaro perpendikular bo‘ladi?
A)1;
3; B) –1; – ![]() ; C) 1;
; C) 1; ![]() ; D) 1; –
; D) 1; – ![]() .
.
3. M (3; –2; 0) va N (–1; 1; 12) nuqtalar orasidagi masofani toping.
A) 10; B) 12; C) 23; D) 13.
4. a (–1;3;2) va b (–2; 4; –3) vektorlarning skalar ko‘paytmasini toping. A) 10; B) 14; C) 8; D) –2.
5. Bir uchi A (3; 4; 8) nuqtada, o‘rtasi C (5; 6; 12) nuqtada bo‘lgan kesmaning ikkinchi uchini toping.
A) (7;8;16); B) (8;7;7); C) (2;2;0); D) (8; 10;1).
6. a (–2; –4; 5) va b (–3; 4; –2) vektorlar berilgan bo‘lsa, ularning ayirmasi a–b ni toping.
A) (–5; 0; 3); B) (1; –8; 7); C) (5; 0; 3); D) (1; 8; 7).
7. Beshburchakli piramidaning nechta uchi bor?
A) 6; B) 5; C) 10; D) 7.
8.
![]()
![]()
![]() Oxy tekisligiga nisbatan (–1; 2; 3) nuqtaga simmetrik bo‘lgan
nuqtani toping.
Oxy tekisligiga nisbatan (–1; 2; 3) nuqtaga simmetrik bo‘lgan
nuqtani toping.
A) (–1; –2; –3); B) (1; 2; –3); C) (–1; 2; –3); D) (1; 2; –3).
9. a (0; –5; 2) va b (2; –3; 1) vektorlar berilgan. 2a – 3b vektorni toping.
A) (–6; –19; 1); B) (–6; –1; 1); C) (0; –4; –1); D) (6; –4; 1).
10. Quyidagi nuqtalardan qaysi biri Oxz tekislikda yotadi?
A) (–4;2;0); B) (0;5;0); C) (2;0;–8); D) (0;–2;1).
11.
![]() a (–4; 2; 2) va b ( 2; − 2;0) vektorlar berilgan bo‘lsa, ular
orasidagi burchakni toping.
a (–4; 2; 2) va b ( 2; − 2;0) vektorlar berilgan bo‘lsa, ular
orasidagi burchakni toping.
A) 60°; B) 150°; C) 135°; D) 120°.
12. Uchlari A (1; –3; –5) va B (5; –1; –3) nuqtalarda bo‘lgan kesma o‘rtasining koordinatalarini toping.
A)
(3; 2;
4); B) (3; –2; –4); ![]() C) (2; –1; 1); D) (2; 1; 1).
C) (2; –1; 1); D) (2; 1; 1).
13. Kub uchun nechta simmetriya tekisligi mavjud?
A) 8; B) 9; C) 7; D) 10.
14. Kubning barcha qirralari yig‘indisi 96. Uning hajmini toping.
A) 256; B) 216; C) 384; D) 4.
15. Kub yog‘ining yuzi 16 ga teng. Kubning hajmini toping.
A) 60; B) 62; C) 66; D) 64.
16. Kubning barcha qirralari yig‘indisi 48 ga teng. Kub sirtining yuzini toping.
A) 96; B) 24; C) 36; D) 48.
17. Agar kubning qirrasi 10% ga kamaytirilsa, uning hajmi necha foiz kamayadi?
A) 10; B) 30; C) 33; D) 27.
18. Qirrasi 1 m bo‘lgan kub qirrasi 1 cm bo‘lgan kublarga ajratildi va ular bir qatorga yig‘ildi. Hosil bo‘lgan qatorning uzunligini toping.
A) 10 m; B) 100 cm C) 10 km; D) 500 m.
19. Asosi kvadrat bo‘lgan to‘g‘ri burchakli parallelepiped uchun nechta simmetriya tekisligi mavjud?
A) 9; B) 7; C) 3; D)5.
20. To‘g‘ri burchakli parallelepiped asosining tomonlari 7 cm va 24 cm. Parallelepipedning balandligi 8 cm. Diagonal kesimining yuzini toping.
A) 168; B) 1344; C) 100; D) 200.
21. O‘lchamlari 21×27×9 bo‘lgan to‘g‘ri burchakli parallelepipedga eng ko‘pi bilan qirrasi 5 ga teng bo‘lgan kublardan nechtasini joylashtirish mumkin (kubning barcha qirralari parallelepipedning qirralariga parallel).
A) 20; B) 25; C) 30; D) 40.
22. Zalning uzunligi, eni va balandliklarining nisbati 5:3:1 kabi. Zalning uzunligi uning enidan 8 m ko‘p. Zalning hajmini (m3) toping.
A) 930; B) 840; C) 960; D) 790.
23. 60 ta qirrasi bo‘lgan prizmaning nechta yog‘i bo‘ladi?
A) 20; B) 21; C) 22; D) 24.
24. Prizmaning jami qirralari 36 ta bo‘lsa, uning nechta yon yog‘i bor?
A) 12; B) 16; C) 9; D) 10.
25.
![]() Prizmaning asosi tomoni 2 5 bo‘lgan muntazam oltiburchakdan, yon
yoqlari kvadratlardan iborat. Prizmaning katta diagonalini toping.
Prizmaning asosi tomoni 2 5 bo‘lgan muntazam oltiburchakdan, yon
yoqlari kvadratlardan iborat. Prizmaning katta diagonalini toping.
A)
![]()
![]() 4 5 ; B)
10; C) 3 5 ; D)
12.
4 5 ; B)
10; C) 3 5 ; D)
12.
26. Uchburchakli to‘g‘ri prizma asosining tomonlari 15, 20 va 25 ga, yon qirrasi asosining eng katta balandligiga teng. Prizmaning hajmini toping.
A) 600; B) 750; C) 3000; D) 1200.
27. Uchburchakli to‘g‘ri prizma asosining tomonlari 13, 14 va 15 ga, yon qirrasi asosining o‘rtacha balandligiga teng. Prizmaning hajmini toping.
A) 336; B) 504; C) 1008; D) 978.
28. O‘q kesimining yuzi 10 ga teng bo‘lgan silindr yon sirtining yuzini toping. A) 10 π; B) 20 π; C) 30 π; D) 15 π.
29. Silindrning balandligi 3 ga, o‘q kesimining diagonali 5 ga teng. Asosining radiusini toping.
A) 2; B) 3; C) 4; D) 5.
30. Silindr o‘q kesimining yuzi 4 ga teng. Yon sirtining yuzini toping. A) 4π; B) 8π; C) 2π; D) 7π.
31. Agar silindrning yon sirti 2 marta orttirilsa, uning hajmi necha marta ortadi?
A) 2; B) 4; C) 8; D) aniqlab bo‘lmaydi.
32. Silindrning hajmi 120 π ga, yon sirti 60 π ga teng. Silindr asosining radiusini toping.
A) 4; B) 5; C) 6; D) 4; 2.
33. To‘rtburchakli muntazam piramidaning balandligi 6 cm, apofemasi esa 6 cm va 5 cm. Piramida asosining perimetrini toping.
A) 10; B) 12; C) 24; D) 20.
34. Muntazam piramida yon sirtining yuzi 96 ga, asosining perimetrini 24 ga teng. Piramidaning apofemasini toping.
A) 16; B) 10; C) 6; D) 8.
35. Uchburchakli muntazam piramidaning balandligi 4 ga, asosining balandligi esa 4,5 ga teng. Piramidaning yon qirrasini toping.
A) 6; B) 6,5; C) 5; D) 5,5.
36. Muntazam piramidaning yon sirti 24 ga, asosining yuzi 12 ga teng. Piramidaning yon yog‘i bilan asos tekisligi orasidagi burchakni toping.
A) 45°; B) 30°; C) 60°; D) 35°.
37. To‘rtburchakli muntazam piramidaning uchidagi tekis burchagi 60° ga teng.
Shu piramidaning yon qirrasi va asosi orasidagi burchakni toping. A) 15°; B) 30°; C) 45°; D) 60°.
38.
![]()
![]() Asosining tomoni 2 ga teng bo‘lgan uchburchakli muntazam
piramidaning to‘la sirti 7 3
dan kichik emas va
13 3 dan katta emas. Shu piramidaning apofemasi qanday
oraliqda yotadi?
Asosining tomoni 2 ga teng bo‘lgan uchburchakli muntazam
piramidaning to‘la sirti 7 3
dan kichik emas va
13 3 dan katta emas. Shu piramidaning apofemasi qanday
oraliqda yotadi?
A)
![]() [2; 3]; B) [ 3 ; 3 3 ]; C) [2 3 ; 4 3 ]; D) [3; 4].
[2; 3]; B) [ 3 ; 3 3 ]; C) [2 3 ; 4 3 ]; D) [3; 4].
39. Piramida asosi to‘g‘ri burchakli uchburchakdan iborat. Uchburchakning katetlari 3 va 4 ga teng. Piramidaning yon yoqlari asos tekisligi bilan 60° li burchaklar hosil qiladi. Piramidaning to‘la sirtini toping.
A) 18; B) 20; C) 15; D) 24.
40. Qirrasi 28 ta bo‘lgan piramidaning yon yoqlari nechta?
A) 12; B) 14; C) 15; D) 18.
41. Hajmi 36 ga teng bo‘lgan to‘rtburchakli muntazam piramidaning asosidagi ikki yoqli burchagi 45°. Piramida asosining tomonini toping.
A) 6; B) 8; C) 4; D) 12.
42. To‘rtburchakli muntazam piramida asosining tomoni 3 marta kattalas htirildi, balandligi esa 3 marta kichiklashtirildi. Hosil bo‘lgan piramida hajmining dastlabki piramida hajmiga nisbatini toping.
A) 3:1; B) 1:3; C) 9:1; D) 1:9.
43. Hajmi 48 bo‘lgan to‘rtburchakli muntazam piramida asosining tomoni 6 ga teng. Piramida yon sirtining yuzini toping.
A) 144; B) 60; C) 72; D) 120.
44. Hajmi 1296 bo‘lgan to‘rtburchakli muntazam piramida asosining tomoni 18 ga teng. Piramida yon sirtining yuzini toping.
A) 540; B) 1080; C) 360; D) 900.
45. Piramidaning yon yoqlari asosi bilan bir xil burchak tashkil etadi. Quyidagi ko‘pburchaklardan qaysi biri piramidaning asosi bo‘lolmaydi?
A) Romb; B) uchburchak; C) kvadrat; D) to‘g‘ri to‘rtburchak.
46.
![]() Hajmi
8 3 ga teng
bo‘lgan muntazam tetraedrning balandligini toping.
Hajmi
8 3 ga teng
bo‘lgan muntazam tetraedrning balandligini toping.
A)
![]()
![]() 2 3 ; B) 3 3 ; C) 4 3 ; D)
4.
2 3 ; B) 3 3 ; C) 4 3 ; D)
4.
47. Oltiburchakli muntazam ABCDEFA1B1C1D1E1F1 (AA1||BB1, …, FF1||AA1) prizmaning EC diagonali va D1 uchi orqali o‘tkazilgan tekislik shu prizmadan ajratgan D1ECD piramidaning hajmi 24 ga teng.
Berilgan prizmaning hajmini toping.
A) 436; B) 428; C) 426; D) 432.
48. To‘rtburchakli muntazam piramida asosining yuzi 36 ga, yon sirtining yuzi esa 60 ga teng. Piramidaning hajmini toping.
A) 64; B) 120; C) 144; D) 72.
49.
![]() O‘nikkiburchakli
muntazam piramidaning apofemasi 2 2 ga teng, barcha yon yoqlari asos tekisligiga 45°
burchak ostida og‘gan. Uning hajmini toping.
O‘nikkiburchakli
muntazam piramidaning apofemasi 2 2 ga teng, barcha yon yoqlari asos tekisligiga 45°
burchak ostida og‘gan. Uning hajmini toping.
A)
![]()
![]()
![]()
![]() 56–30 2 ; B) 64–32
3 ; C) 68–48 2 ; D) 64–32 2 .
56–30 2 ; B) 64–32
3 ; C) 68–48 2 ; D) 64–32 2 .
50. To‘rtburchakli muntazam kesik piramida asoslarining tomonlari 14 va 10 cm, diagonali 18 cm. Kesik piramidaning balandligi necha cm? A) 6; B) 7; C) 8; D) 5.
51. Piramidaning balandligi 8 ga teng. Piramida uchidan 4 ga teng masofada asosga parallel tekislik o‘tkazilgan va hosil bo‘lgan kesim yuzi 27 ga teng. Piramida hajmini toping.
A) 480; B) 210; C) 92; D) 288.
52. To‘rtburchakli muntazam piramidaning balandligi 8 ga, asosining tomoni 12 ga teng. Piramida yon yog‘iga parallel bo‘lib, asosining markazi orqali o‘tgan kesimi yuzini hisoblang.
A) 45; B) 60; C) 72; D) 30.
53. Konus asosining radiusi 0,5 ga teng. Konus yasovchisi bilan uning asos tekisligi orasidagi burchak qanday bo‘lganda konus yon sirtining yuzi 0,5π ga teng bo‘ladi?
A) 30°; B) 60°; C) 45°; D) arccos (1/3).
54. ![]()
![]() Konus asosining radiusi 3 /2 ga teng.
Konus yasovchisi bilan uning asos tekisligi orasidagi burchak qanday bo‘lganda
konus yon sirtining yuzi 3 π /2 ga teng bo‘ladi?
Konus asosining radiusi 3 /2 ga teng.
Konus yasovchisi bilan uning asos tekisligi orasidagi burchak qanday bo‘lganda
konus yon sirtining yuzi 3 π /2 ga teng bo‘ladi?
A)
![]() arccos
(1/ 3 );
B) arccos (1/3); C) 45°; D) 30°.
arccos
(1/ 3 );
B) arccos (1/3); C) 45°; D) 30°.
55. Konusning yon sirti 60π ga, to‘la sirti 96π ga teng. Konusning yasovchisini toping.
A) 12; B) 9; C) 8; D) 10.
56. Katetlari 6 va 8 ga teng bo‘lgan to‘g‘ri burchakli uchburchakning kichik kateti atrofida aylanishidan hosil bo‘lgan jismning to‘la sirtini toping.
A) 144π; B) 100π; C) 80π; D) 150π.
57. Konusning to‘la sirti asosining yuzidan 3 marta katta bo‘lsa, o‘q kesimining uchidagi burchagini toping.
A) 60°; B) arccos (7/9); C) 45°; D) 30°.
58. Konus o‘q kesimining ikki tomoni 4 va 9 ga teng. Shu konusning yon sirtini toping.
A) 12π; B) 16π; C) 18π; D) 24π.
59.
![]() Asos
aylanasining uzunligi 8 pga, balandligi 9
cm ga teng bo‘lgan konusning hajmini toping.
Asos
aylanasining uzunligi 8 pga, balandligi 9
cm ga teng bo‘lgan konusning hajmini toping.
A) 16π; B) 24; C) 16; D) 48.
60. Konusning o‘q kesimi muntazam uchburchakdan, silindrniki esa kvadratdan iborat. Agar ularning hajmlari teng bo‘lsa, to‘la sirtlarining nisbati nimaga teng?
A)
![]()
![]()
![]() 2 : 3 ;
B) 2 3 : 3 2 ; C) 3 :
2; D) 1 : 2 3 .
2 : 3 ;
B) 2 3 : 3 2 ; C) 3 :
2; D) 1 : 2 3 .
61. y =|x – 1|, x = –1, x = 2 va y = 0 chiziqlar bilan chegaralangan shaklning abssissalar o‘qi atrofida aylanishidan hosil bo‘lgan jismning hajmini toping.
A) 3π; B) 4π; C) 5π; D) π.
62. Konus hajmi 9π ga teng bo‘lib, uning yasovchisi asos tekisligi bilan 45° li burchak tashkil qiladi. Konusning balandligini toping.
A)
![]() 3;
B) 2; C) 3 ;
D) 1,5.
3;
B) 2; C) 3 ;
D) 1,5.
63. Konusning balandligi 6 ga teng. Konusning asosidan 4 ga teng masofada unga parallel tekislik o‘tkazilgan. Hosil bo‘lgan kesim yuzining konus asosi yuziga nisbatini toping.
A) 1/3; B) 2/3; C) 4/9; D) 1/9.
64. Kesik konus asoslarining radiuslari 1 va 5 ga teng. Agar uning balandligi 3 ga teng bo‘lsa, yasovchisini toping.
A) 6; B) 3; C) 4; D) 5.
65. Agar sferaning radiusi 50% orttirilsa, sfera sirtining yuzi necha foizga ko‘payadi?
A) 125; B) 100; C) 150; D) 75.
66. ![]() Radiusi 13 ga teng bo‘lgan
shar tekislik bilan kesilgan. Agar shar markazidan kesimgacha masofa 10 ga teng
bo‘lsa, kesimning yuzini toping. A) 69π; B) 3 6 π; C)
100π; D) 3.
Radiusi 13 ga teng bo‘lgan
shar tekislik bilan kesilgan. Agar shar markazidan kesimgacha masofa 10 ga teng
bo‘lsa, kesimning yuzini toping. A) 69π; B) 3 6 π; C)
100π; D) 3.
67. Radiuslari 2, 3 va 4 ga teng bo‘lgan metall sharlar eritilib, bitta shar quyildi. Shu sharning hajmini toping.
A) 144π; B) 396π; C) 99π; D) 132π.
68.
![]() Sharning
radiusi 8 π
ga teng. Radiusning oxiridan u bilan 60° li burchak tashkil etadigan
kesuvchi tekislik o‘tkazilgan. Kesimning yuzini toping.
Sharning
radiusi 8 π
ga teng. Radiusning oxiridan u bilan 60° li burchak tashkil etadigan
kesuvchi tekislik o‘tkazilgan. Kesimning yuzini toping.
A) 8; B) 12; C) 16; D) 14.
69. Sharni bo‘yash uchun 50 massa birligida bo‘yoq ishlatildi. Agar sharning diametri ikki marta orttirilsa, uni bo‘yash uchun qancha bo‘yoq kerak bo‘ladi?
A) 100; B) 125; C) 150; D) 200.
70. Shardan tashqaridagi M nuqtadan uning sirtiga MN urinma o‘tkazildi. M nuqtadan sharning sirtigacha bo‘lgan eng qisqa masofa 6 ga, sharning markazigacha bo‘lgan masofa 15 ga teng. MN ning uzunligini toping.
A) 10; B) 16; C) 14; D) 12.
71. Kovak shar devorining hajmi 252π ga, devorning qalinligi 3 ga teng.
Ichki sharning radiusini toping.
A) 5; B) 3; C) 4; D) 7.
72. Shar radiusi 6 ga teng. Radius uchidan 30° burchak tashkil qiluvchi tekislik o‘tkazilgan. Shar bilan tekislik hosil qilgan kesimning yuzini toping.
A) 27π; B) 8π; C) 64π; D) 25π.
73. Radiusi 15 ga va 20 ga teng bo‘lgan ikki shar markazlari orasidagi masofa 25 ga teng. Shar sirtlari kesishishidan hosil bo‘lgan aylananing uzunligini toping.
A) 24π; B) 20π; C) 25π; D) 15π.
74. To‘la sirtining yuzi 72 ga teng bo‘lgan kubga tashqi chizilgan sharning radiusini toping.
A)
![]()
![]() 3; B) 6; C)
3 3 ; D)
2 3 .
3; B) 6; C)
3 3 ; D)
2 3 .
75. Hajmi 125 bo‘lgan kubga ichki chizilgan shar sirtining yuzini toping.
A) 125π; B) 25π; C) 24,5π; D) 105π.
76. ![]() Ikkita qo‘shni yoqlarining
markazlari orasidagi masofa 2 2 ga teng bo‘lgan kubga tashqi chizilgan shar sirtining
yuzini toping.
Ikkita qo‘shni yoqlarining
markazlari orasidagi masofa 2 2 ga teng bo‘lgan kubga tashqi chizilgan shar sirtining
yuzini toping.
A)
![]() 28π;
B) 36π; C) 48π; D) 18 2 π.
28π;
B) 36π; C) 48π; D) 18 2 π.
77. Kubning qirrasi 6 ga teng. Kubga ichki chizilgan sharning hajmini toping.
A) 12π; B) 36π; C) 27π; D) 18π.
78. ![]() Oktaedr sirtining yuzi 24 3 cm2 ga teng bo‘lsa, uning
qirrasini toping.
Oktaedr sirtining yuzi 24 3 cm2 ga teng bo‘lsa, uning
qirrasini toping.
A)
![]()
![]() 2 3 cm; B) 2 2 cm; C) 2 cm; D) 2 6 cm.
2 3 cm; B) 2 2 cm; C) 2 cm; D) 2 6 cm.
79. Piramidaning to‘la sirti 60 ga, unga ichki chizilgan sharning radiusi 5 ga teng. Piramidaning hajmini toping.
A) 120; B) 80; C) 90; D)100.
80. Oltiburchakli muntazam piramidaning apofemasi 5 ga, uning asosiga tash qi chizilgan doiraning yuzi 12π ga teng. Shu piramidadagi ichki chizilgan sharning radiusini toping.
A) 3; B) 3,2; C) 1,5; D) 2,5.
81. Muntazam tetraedrning qirrasi 1 ga teng. Shu tetraedrga tashqi chizilgan sharning radiusini toping.
A)
![]()
![]()
![]()
![]() 2 2 /3; B) 6 /4; C) 3 2 /8; D)11 2 /24.
2 2 /3; B) 6 /4; C) 3 2 /8; D)11 2 /24.
82. To‘rtburchakli muntazam kesik piramida kichik asosining yuzi 50 ga, katta asosining yuzi 200 ga teng. Shu piramidaga ichki chizilgan sfera sirtining yuzini toping.
A) 96π; B) 125π; C) 120π; D)100π.
83. O‘q kesimi kvadratdan iborat silindrga ichki chizilgan sharning hajmi 9π/16 ga teng. Silindrning yon sirtini toping.
A) 3π/4; B) 7π/4; C) 9π/4; D) 5π/4.
84. Silindrga shar ichki chizilgan. Silindrning hajmi 16p ga teng bo‘lsa, sharning hajmini toping.
A) 32π/3; B) 16π/3; C) 64π/3; D)16π.
85. Radiusi 1 ga teng bo‘lgan sferaga ichki chizilgan eng katta hajmli silindrning balandligini toping.
A)
![]()
![]()
![]()
![]() 3 3 /4; B) 3 /2; C)
2 3 /3; D)
2 /3.
3 3 /4; B) 3 /2; C)
2 3 /3; D)
2 /3.
86. O‘q kesimi kvadratdan iborat silindr shaklidagi g‘o‘ladan eng katta hajmdagi shar yo‘nib olindi. G‘o‘laning qancha foizi chiqitga ketgan?
A)
25; B) 30; C) 33![]() ; D)37
; D)37![]() .
.
87.
![]() Sharga
ichki chizilgan konusning balandligi 3 ga, asosining radiusi 3 3 ga teng. Sharning
radiusini toping.
Sharga
ichki chizilgan konusning balandligi 3 ga, asosining radiusi 3 3 ga teng. Sharning
radiusini toping.
A)
![]()
![]() 5; B) 6; C)
4 3 ; D)
5 2 .
5; B) 6; C)
4 3 ; D)
5 2 .
88. Sharga ichki chizilgan konusning asosi sharning eng katta doirasidan iborat. Sharning hajmi konusning hajmidan necha marta katta?
A) 2; B) 4; C) 3; D) 1,5.
89. Konusning balandligi 6 ga, yasovchisi 10 ga teng. Konusga ichki chizilgan sharning radiusini toping.
A)
![]() 3;
B) 2
3;
B) 2![]() ; C) 4; D) 3 3 .
; C) 4; D) 3 3 .
90. Sharga konus shunday ichki chizilganki, konusning yasovchisi asosining diametriga teng. Konusning to‘la sirti shar sirti yuzining necha foizini tashkil etadi?
A) 62; B) 56,25; C) 54,5; D) 60,75.
91. Kesik konus asoslarining yuzlari 9π va 25π ga teng. Agar bu konusga sharni ichki chizish mumkin bo‘lsa, konusning yon sirtini toping. A) 80π; B) 36π; C) 54π; D) 64π.
92. Yasovchisi 5 ga, asosining diametri 6 ga teng bo‘lgan konusga ichki chizilgan shar sirtining yuzini toping.
A) 16π; B) 64 π/11; C) 9π; D) 71π/9.
93. Kesik konusga shar ichki chizilgan. Agar kesik konus asoslarining yuzlari π va 4π ga teng bo‘lsa, shu konus yon sirtining yuzini toping.
A) 6π; B) 7π; C) 8π; D) 9π.
94. Radiusi 4 ga teng bo‘lgan sharga balandligi 9 ga teng bo‘lgan konus tashqi chizilgan. Konus asosining radiusini toping.
A) 12; B) 9; C) 10; D) 8.
95. Teng tomonli konusga shar tashqi chizilgan. Shar sirtining konusning to‘la sirtiga nisbatini toping.
A) 9 : 4; B) 7 : 4; C) 16 : 9; D) 4 : 3.
96. Konus asosining yuzi 9π ga, yon sirtining yuzi 15π ga teng. Shu konusga ichki chizilgan sferaning radiusini toping.
A) 1,5; B) 1,8; C) 2; D) 2,4.
97. Silindr va unga tashqi chizilgan to‘rtburchakli muntazam parallelepiped asosining tomoni 4 ga teng. Silindrning hajmini toping.
A) 10π; B) 12π; C) 16π; D) 20π.
98. Kubga konus ichki chizilgan. Agar konusning asosi kubning ostki asosiga ichki chizilgan bo‘lsa, uchi esa yuqoridagi asosining markazida yotsa, konus va kub hajmlari nisbatini toping.
A) π/2; B) π/3; C) π/6; D) π/12.
Yakuniy nazorat ishi namunasi
1variant
1.
![]() Uchta
nuqta berilgan: A (1; 1; 1), B (–1; 0; 1), C (0; 1; 1).
Shunday D (x; y; z) nuqtani topingki, AB va CD vektorlar
teng bo‘lsin.
Uchta
nuqta berilgan: A (1; 1; 1), B (–1; 0; 1), C (0; 1; 1).
Shunday D (x; y; z) nuqtani topingki, AB va CD vektorlar
teng bo‘lsin.
![]()
![]() A) D (2; 0; 1); B) D (–2;
0; 1); C) D (–2; 1; 1); D) D (2; 0; 0).
A) D (2; 0; 1); B) D (–2;
0; 1); C) D (–2; 1; 1); D) D (2; 0; 0).
2. Skalar ko‘paytmasi 0,5 ga teng bo‘lgan birlik vektorlar orasidagi burchakni toping.
A) 60°; B) 30°; C) 120°; D) 45°.
3.
![]() Kubning
ikkita qaramaqarshi yoqlarining diagonallari orqali o‘tkazilgan kesimning yuzi
16 2 ga
teng. Kubning qirrasini toping.
Kubning
ikkita qaramaqarshi yoqlarining diagonallari orqali o‘tkazilgan kesimning yuzi
16 2 ga
teng. Kubning qirrasini toping.
![]() A)
4; B) 2 2 ; C) 4 2 ; D) 8.
A)
4; B) 2 2 ; C) 4 2 ; D) 8.
4. Muntazam uchburchakli prizmaning hajmi 27 3 ga, asosiga tashqi chizilgan aylananing radiusi esa 2 ga teng. Prizmaning balandligini toping.
A) 12; B) 8; C) 6; D) 9.
5. Oktaedrning qirrasi a ga teng. Uning to‘la sirtini hisoblang.
![]()
![]()
![]()
![]() A)
2a2 3 ; B)
a2 3 ; C)
2 3a2 / 3; D)
4a2 3 .
A)
2a2 3 ; B)
a2 3 ; C)
2 3a2 / 3; D)
4a2 3 .
6. To‘rtburchakli muntazam kesik piramidaning balandligi 16 ga, asoslarining tomonlari 24 va 40 ga teng. Kesik piramidaning diagonalini toping.
A) 48; B) 24; C) 36; D) 40.
7. Konusning balandligi 10 ga, o‘q kesimi uchidagi burchagi 120° ga teng.
Konus hajmini toping.
A) 1000p; B) 1200p; C) 900p; D) 600p.
8. Shar katta doirasining yuzi 25π ga teng. Sharning markazidan qanday masofada o‘tkazilgan tekislik shardan doirasining yuzi 9π ga teng bo‘lgan kesim ajratadi?
A) 3,8; B) 3,6; C) 3,5; D) 4.
9. Piramidaning hajmi 25 ga, unga ichki chizilgan sharning radiusi 1,5 ga teng. Piramidaning to‘la sirtini toping.
A) 20; B) 15; C) 25; D)50.
10. Balandligi 3 ga, yasovchisi 6 ga teng bo‘lgan konusga tashqi chizilgan sharning radiusini toping.
![]()
![]() A)
3 3 ; B)
5; C) 6; D) 4 2 .
A)
3 3 ; B)
5; C) 6; D) 4 2 .
2variant
1.
![]()
![]() Uchta nuqta berilgan: A (2
1; –1), B (–3; 1; 1), C (2; 0; 1). ShundayD(x; y;
z) nuqtani topingki, AB va CD vektorlar teng bo‘lsin.
Uchta nuqta berilgan: A (2
1; –1), B (–3; 1; 1), C (2; 0; 1). ShundayD(x; y;
z) nuqtani topingki, AB va CD vektorlar teng bo‘lsin.
A) D (3; 0; 1); B) D (–3; 0; 1); C) D (–3; 0; 3); D) D (–3; 0; 0).
2.
![]() Skalar
ko‘paytmasi ga teng bo‘lgan birlik vektorlar orasidagi burchakni toping.
Skalar
ko‘paytmasi ga teng bo‘lgan birlik vektorlar orasidagi burchakni toping.
A) 60°; B) 30°; C) 120°; D) 45°.
3.
![]() To‘rtburchakli
muntazam prizma asosining tomoni 2 ga, diagonali bilan yon yog‘i orasidagi burchak esa
30° ga teng. Prizmaning hajmini toping.
To‘rtburchakli
muntazam prizma asosining tomoni 2 ga, diagonali bilan yon yog‘i orasidagi burchak esa
30° ga teng. Prizmaning hajmini toping.
![]()
![]() A)
8 2 ; B)
4; C) 16; D) 4 2 .
A)
8 2 ; B)
4; C) 16; D) 4 2 .
4.
![]() Silindrning
balandligi 5 ga, uning asosiga ichki chizilgan muntazam uchburchakning tomoni 3
3 ga teng. Silindrning
hajmini toping. A) 25π; B) 35π; C) 45π; D)
40π.
Silindrning
balandligi 5 ga, uning asosiga ichki chizilgan muntazam uchburchakning tomoni 3
3 ga teng. Silindrning
hajmini toping. A) 25π; B) 35π; C) 45π; D)
40π.
5.
![]() To‘rtburchakli
muntazam piramidaning yon qirrasi 3 2 ga, yon qirra va asos tekisligi orasidagi burchak
45° ga teng. Piramidaning hajmini toping.
To‘rtburchakli
muntazam piramidaning yon qirrasi 3 2 ga, yon qirra va asos tekisligi orasidagi burchak
45° ga teng. Piramidaning hajmini toping.
![]()
![]() A)
12 2 ; B)
18; C) 9 2 ; D) 24.
A)
12 2 ; B)
18; C) 9 2 ; D) 24.
6. Konusning yasovchisi 15 ga, yon sirti yoyilmasining uchidagi burchagi 120° ga teng. Konus asosining diametrini toping.
A) 10; B) 15; C) 20; D) 25.
7. Asoslarning radiuslari 2 va 7 ga, o‘q kesimining diagonali 15 ga teng bo‘lgan kesik konus yon sirtining yuzini toping.
A) 112π; B) 115π; C) 117π; D) 120π.
8. Kubga tashqi chizilgan sharning hajmi unga ichki chizilgan sharning hajmidan necha marta katta?
![]()
![]() A)
8; B) 4; C) 4 2 ; D) 3 3 .
A)
8; B) 4; C) 4 2 ; D) 3 3 .
9. Silindrga shar ichki chizilgan. Silindrning hajmi 16π ga teng bo‘lsa, sharning hajmini toping.
A) 32π/3;
B) 16π/3; C) 64π/3;
D)10![]() π.
π.
10. Qirrasi 12 ga teng bo‘lgan kubga konus ichki chizilgan. Konusning asosi kubning quyi asosiga ichki chizilgan, uchi esa kubning yuqoridagi asosining markazida. Konusning hajmini toping.
A) 120π; B) 132π; C) 126π; D) 144π.
![]() 349. 20 cm. 350. 2
cm. 351. 32 cm2.
352. 36 cm2.
360. 576 cm2.
361. 2 cm. 376. 6 cm. 377. 3 cm. 378. 48 cm. 379. 576
cm2. 380. 2 cm. 381. 6
2 . 382. 8.
349. 20 cm. 350. 2
cm. 351. 32 cm2.
352. 36 cm2.
360. 576 cm2.
361. 2 cm. 376. 6 cm. 377. 3 cm. 378. 48 cm. 379. 576
cm2. 380. 2 cm. 381. 6
2 . 382. 8.
383. 168. 384. 4.
385. 2 cm. 386. 36 cm. ![]()
406. 2592100 m3. 407. ≈50°. 408. 9. 414. 84 dm. 421. 12 cm. 426. 48 cm2.
427. 320p cm2. 437. 4 cm. 440. 144p cm2. 441. 100p dm2. 442. 96 cm2.
![]()
![]()
![]() 27 11 2. 444. 576p cm2. 445.p. 446. 36p cm2.
447. 16 3 p cm2.
27 11 2. 444. 576p cm2. 445.p. 446. 36p cm2.
447. 16 3 p cm2.
443. cm
8
449. 30π. 450. 132π.
455. 65p cm2. 456. 160p
cm2. 458. 129p
cm3. 459. ![]() p cm2.
p cm2.
![]() 875 3 2. 476. 45°. 477. (1; 2). 478. arccos 5/12. 480. 54.
481. 60°.
875 3 2. 476. 45°. 477. (1; 2). 478. arccos 5/12. 480. 54.
481. 60°.
460. p cm
3
![]() 483. 2 13 . 484. Romb. 485. 6
3. 486. 24. 487. 2,5.
488. 30°. 489. 3.
483. 2 13 . 484. Romb. 485. 6
3. 486. 24. 487. 2,5.
488. 30°. 489. 3.
![]()
![]() 490. 60°. 491. 36. 492. l3 2tga .493. 4. 494. 448. 495. 75. 496. 32π.
497.
2 πR2.
490. 60°. 491. 36. 492. l3 2tga .493. 4. 494. 448. 495. 75. 496. 32π.
497.
2 πR2.
498. 360. 499. 108°. 500. 216°. 501. 48π. 502. 4π. 503. 100π. 504. 8π 3 /3. 505. 135π. 506. 72π.
3test sinovi javoblari
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
D |
D |
C |
C |
A |
A |
B |
C |
D |
C |
A |
B |
D |
B |
A |
|
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
C |
B |
A |
A |
B |
D |
B |
B |
B |
A |
A |
D |
C |
B |
A |
3nazorat ishi javoblari: 1) 5; 2) 640; 3) 7 cm; 4) 216°; 5) 24π.
507. a) 1 yoki 2ta; b) 1 ta yoki cheksiz ko‘p. 508. 1447p dm2. 590. 25 p cm2. 510. O( –1; 2; 1), R = 5. 511. (x – 5)2+(y + 2)2 + (z – 7)2 = 4. 512. (x – 3)2 + (y + 2)2 + (z – 1)2 = 18. 513. (x – 3)2 + (y + 1)2 + (z – l)2 = 2I.
514. 6 dm. 515. 15 s. 516.24. 517. 8. 518. 3. 519. 12. 520. 4. 521. 5. 522. 5. 523. 27π. 524. 24π. 526. 150. 527. 2. 528. R+r. 529. 254%. 530. 3. 531.
![]()
![]() 4 3 . 532. 6 /4. 533. 240. 534. 50.
535. 6. 536. 32π.
537.
4 3 . 532. 6 /4. 533. 240. 534. 50.
535. 6. 536. 32π.
537. ![]() p. 555. 4000p/3 cm3
= 4/3p dm3. 564. 252p cm3,
720p cm3. 565. 500/3p.
p. 555. 4000p/3 cm3
= 4/3p dm3. 564. 252p cm3,
720p cm3. 565. 500/3p.
![]()
![]()
![]()
![]() 1 4 3 500
1 4 3 500
566. p. 567. ![]() p. 568. p. 569.
p. 568. p. 569. ![]() p. 570. p. 571. p. 573. 4,5p.
p. 570. p. 571. p. 573. 4,5p.
6 27 3 3 2
574. 4,5p. 575. 22. 576. 36. 588. 7. 589. 24. 606. Birinchisini. 611. 8 marta, 4 marta. 613. 12. 616. 9 marta. 620.10p.
![]() 626. 160000. 627. 10cm. 628. 27 cm. 629. 6 cm. 630. 26. 631. ≈6 dm3. 632. 12. 635.
1,28π. 636. 0,9025π. 638. 27 marta. 639. 12. 640. 9 marta. 641. 10.
626. 160000. 627. 10cm. 628. 27 cm. 629. 6 cm. 630. 26. 631. ≈6 dm3. 632. 12. 635.
1,28π. 636. 0,9025π. 638. 27 marta. 639. 12. 640. 9 marta. 641. 10. ![]() 144. 665. 3
3 H (4R2– H2)/16.
144. 665. 3
3 H (4R2– H2)/16.
![]() 32:9.
32:9.
![]() .
.
682. 144π. 683. 2. 684. π/4. 685. 144π. 686. 18π. 687. 12/π. 688. 512π. 689. 24.
4test sinovi javoblari
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
A |
D |
A |
A |
A |
B |
B |
B |
C |
A |
A |
D |
D |
D |
C |
|
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
D |
B |
C |
C |
A |
D |
A |
C |
B |
D |
D |
B |
D |
C |
D |
4nazorat ishi javoblari: 1) 64; 2) 1; 3) 9π/4; 4) 36π; 5) 0,75.
Takrorlash testi javoblari
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
B |
C |
D |
C |
A |
B |
A |
B |
A |
C |
D |
B |
B |
D |
D |
|
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
A |
D |
C |
D |
D |
A |
C |
C |
A |
B |
C |
C |
A |
A |
A |
|
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
|
D |
A |
D |
D |
C |
C |
C |
C |
A |
B |
A |
A |
B |
A |
D |
|
46 |
47 |
48 |
49 |
50 |
51 |
52 |
53 |
54 |
55 |
56 |
57 |
58 |
59 |
60 |
|
D |
D |
D |
B |
A |
D |
A |
B |
D |
D |
A |
A |
C |
D |
B |
|
61 |
62 |
63 |
64 |
65 |
66 |
67 |
68 |
69 |
70 |
71 |
72 |
73 |
74 |
75 |
|
A |
A |
D |
D |
A |
D |
D |
C |
D |
D |
B |
A |
A |
A |
B |
|
76 |
77 |
78 |
79 |
80 |
81 |
82 |
83 |
84 |
85 |
86 |
87 |
88 |
89 |
90 |
|
C |
B |
A |
D |
C |
B |
D |
C |
A |
C |
C |
B |
C |
B |
B |
|
91 |
92 |
93 |
94 |
95 |
96 |
97 |
98 |
|
|
|
|
|
|
|
|
D |
D |
D |
A |
C |
A |
B |
D |
Yakuniy nazorat ishi javoblari
|
1variant |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
B |
A |
A |
B |
D |
C |
A |
B |
A |
A |
|
|
2variant |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
C |
D |
A |
C |
D |
D |
D |
A |
C |
D |
1. A’zamov A., Xaydarov B. Matematika sayyorasi.–T., O‘qituvchi, 1993.
2. Afonina S.I. Matematika va qo‘zallik.–T., O‘qituvchi, 1986.
3. Norjigitov X. Mirzayev Ch. Stereometrik masallarni yechish. Akademik litseylar uchun o‘quv qo‘llanma.–T., 2004.
4. Israilov I., Pashayev Z. Geometriya. Akademik litseylar uchun o‘quv qo‘llanma.
II qism.–T., O‘qituvchi, 2005.
5. Александров А. Д., Вернер А, Л., Рыжик В, И. Геометрия для 10–11х классов:
учеб. пособие для учащихся шк. и классов с углубленным изучением математики, – 3е. изд.–М., Просвещение, 1992. – 464 с.
6. Киселев А. П. Элементарная геометрия. Книга для учителя / А. П. Киселев. – М.: Просвещение, 1980. – 287 с.
7. Погорелов А.В. “Геометрия 10–11”, учебник. –М., Просвешение, 2009.
8. Л. А. Латотин, Б. Д. Чеботаревский. “Математика 11”, учебник.–Минск, 2013.
9. Смирнова И.М., Смирнов В.А. Геометрия. 10–11 класс. учебник. –М., 2008.
10. Бевз Г. П. Геометрия: Учебник для 7–11 кл. / Г. П. Бевз, В. Г. Бевз, Н.Г. Владимирова. –М., Просвещение, 1990.
11. А. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. Геометрия: Учеб. для 10 – 11 кл. общеобразоват. учреждений. М., Просвещение, 1998.
12. Смирнова И. –М. Геометрия: учебное пособие для 10–11 кл. гуманит. профиля. / И. М. Смирнова. М., Просвещение, 1997.
13. Шарыгин И. Ф. Геометрия 10 – 11 классы. / И. Ф. Шарыгин // Математика – 2006 – №3 – С. 36–38.
14. Билянина О.Я. и др. “Геометрия 11” учебник. –Киев, “Генеза”, 2010.
15. Daniel C.Alexander, Elementary geometry for college students, Canada, Brooks / Cole, Cengage Learning, 2011.
16. Mal Coad and others, Mathematics for the international students, Haese and Harris publocations, Australia, 2010.
17. http://www.uzedu.uz – Xalq ta’limi vazirligining axborot ta’lim portali.
18. http://www.eduportal.uz – Multimedia markazi axborot ta’lim portali.
19. http://www.school.edu.ru – Umumta’lim portali (rus tilida).
20. http://www.problems.ru/ Matematikadan masalalar izlash tizimi (rus tilida).
21. http://geometry.net / – Algebra va geometriyadan o‘quv materiallari (ingliz tilida).
22. http://www.ixl.com – Masofadan turib o‘qitish sayti (ingliz tilida).
23. http://www.mathkang.ru – “Kenguru” xalqaro matematik tanlov sayti (rus tilida).
24. http://www.khanakademy. org –”Xon akademiyasi” masofaviy ta’lim sayti (ingliz tilida).
25. http://www.brilliant.org – Matematikadan masofaviy ta’lim sayti (ingliz tilida).
III BOB. PIRAMIDA VA KONUS
10. Piramida va kesik piramida ..................................................... 113
11. Konus va kesik konus ............................................................... 127
12. Bobni takrorlashga doir amaliy mashqlar .............................. 140
IV BOB. SFERA VA SHAR
13. Shar va uning elementlari ........................................................ 146
14. Shar va uning bo‘laklari hajmi ..................................................155
15. Sfera sirtining yuzi .................................................................. 165 16. Bobni takrorlashga doir amaliy mashqlar ............................... 171
V BOB. TAKRORLASH
17. Stereometriyani takrorlashga doir test topshiriqlari ................ 177
JAVOBLAR ................................................................................... 188
Darslikni tuzishda foydalanilgan
va qo‘shimcha o‘rganishga tavsiya etilayotgan adabiyotlar va elektron
resurslar .................... 190
Algebra va analiz asoslari: M.A. Mirzaahmedov, Sh.N. Ismailov, A.Q. Amanov.
Geometriya: B.Q. Xaydarov.
MATEMATIKA 11
ALGEBRA VA ANALIZ ASOSLARI,
GEOMETRIYA
II QISM
O‘rta ta’lim muassasalarining 11sinfi va o‘rta maxsus, kasbhunar ta’limi muassasalari o‘quvchilari uchun darslik
1 nashr
Muharrirlar: N. Gayipov
M. Raemov
Texnik muharrir: A. Abdusalomov
Kompyuterda sahifalovchi: S. G‘ofurov
Nashriyot litsenziyasi AI № 015. 20.07.2018 Bosishga ruxsat etildi 05.09.2018. Bichimi 70×1001/16
“Times New Roman” garniturasi.
Hajmi: 12,0 bosma tab. Nashr tab. 11,0.
Adadi 433091 nusxada
Originalmaket “Zamin Nashr” MCHJ da tayyorlandi. 100053, Toshkent sh.
Bog‘ishamol ko‘chasi, 160. Tel: 235 44 82 Buyurtma № 18334.
O‘zbekiston matbuot va axborot agentligi "O‘ZBEKISTON" nashriyotmatbaa ijodiy uyi. 100011, Toshkent sh., Navoiy 30.
Tel.: (371) 2448755, 2448720
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.