
|
Дата: |
ФИО учителя: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Класс:8 |
Количество присутствующих: |
отсутствующих: |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Тема урока |
Квадратныйтрехчлен |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу) |
8.2.1.1 усвоить понятие корня квадратного трехчлена; |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Целиурока |
− −объяснить понятие корня квадратного трехчлена; |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Критерии успеха |
− знает понятие корня квадратного трехчлена; − решает квадратные уравнения; − владеет навыками самообучения. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Языковыецели
|
Учащиеся будут: − комментировать решение квадратного или дробно–рационального уравнения; − аргументировано рассуждать о количестве корней квадратного уравнения;
Лексика и терминология, специфичная для предмета: − квадратныйтрехчлен; − кореньквадратноготрехчлена; − квадратноеуравнение; − уравнениевторойстепени; − полное и неполное квадратные уравнения; − приведенноеквадратноеуравнение; − первый или старший коэффициент, второй коэффициент или коэффициент при х, свободный член; − дискриминант; − выделениеквадратадвучлена; − рациональноеуравнение; − биквадратноеуравнение; − область допустимых значений дробно–рационального уравнения; − постороннийкорень. Полезные выражения для диалогов и письма: − представим левую часть уравнения в виде квадрата двучлена…; − дискриминантомквадратногоуравненияназывается…; − данное квадратное уравнение имеет … (количество корней), так как…; − сумму и произведение корней произвольного квадратного уравнения можно выразить через…; − корни данного квадратного уравнения одного знака, так как…; − корни данного квадратного уравнения разного знака, так как…; − данный корень является посторонним, так как…. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Привитиешкольных ценностей |
Сотрудничество. Академическая честность. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Взаимосвязь с «Мәңгілік ел» |
Привитие таких ценностей, как осуществляется через работу в паре и при индивидуальной работе. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Межпредметныесвязи |
Прикладная математика, физика |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Навыкииспользования ИКТ |
Развитие навыков работы с ИД. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Предварительныезнания
|
Знание определения квадратного корня и арифметического квадратного корня, умение находить квадратные корни, вычислять значения иррациональных выражений, упрощать целые и иррациональные выражения. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Тип урока: |
Урок изучения нового и закрепления знаний. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ходурока |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Запланированныеэтапыурока |
Запланированнаядеятельностьнауроке |
Ресурсы |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Началоурока 1 мин.
2 мин |
1. Организационный момент. (1 мин.) Приветствие. Проверка подготовленности к уроку: наличие учебника, тетради, принадлежностей.
Повторение: (слайд 1-5) На доске записано: - Что написано на доске? - От чего зависит
количество корней? - Как найти корни квадратного уравнения? |
Учебная литература: 1) Алгебра 8. Шыныбеков А.Н. Учебник для 8 класса общеобразовательной школы. 3-е изд. – Алматы: Атамұра, 2012. – 288 с. ISBN 978-601-282-527-5 Глава 2. п.1 стр. 61-63
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
20 минут
10 мин
10мин.
7 мин.
2 урок
10мин.
10-15мин.
2мин.
10мин.
1 мин. |
Деление на группы с помощью палочек(палочки двух цветов). Игра «Тарсия». (15-20мин) Приложение 1 Решите уравнение:
Новая тема. (Слайд 6) Найдем
значение квадратного трехчлена
При х=2 квадратный трехчлен 3х2-7х+2 обращается в нуль. Такое значение переменной называют корнем квадратного трехчлена. Определение: Корнем квадратного трехчлена называется значение переменной, при котором значение квадратного трехчлена равно нулю. Чтобы
найти корни квадратного трехчлена Найдем,
например, корни квадратного трехчлена
Значит,
квадратный трехчлен Число корней квадратного
трехчлена В зависимости от дискриминанта квадратный трехчлен так же, как квадратное уравнение, может иметь два корня, один корень(или два одинаковых корня) или вовсе не иметь корней. Корни квадратного трехчлена можно использовать при его разложении на множители. Закрепление знаний.
Можно предложить учащимся индивидуальную «Карточку–шифровку» на применение определения корня квадратного трехчлена. Из предложенных значений переменной к каждому трехчлену необходимо выбрать то значение, которое является его корнем, и выписать буквы кода в соответстии с нумерацией трехчленов. Для удобства результаты можно записать в таблицу и получить фамилию первого казахского профессора – математика.
Ответ: ЕРМЕКОВ Алимхан Абеуович (1891–1970).
Работа со всем классом. (Слайд8) По учебнику Макарычева 8 класс. 24.36 Найдите корни квадратного трехчленаа)
№59.Найдите корни квадратного трехчлена:
Парная работа. (слайд 9) №60
№362.
Гимнастика для глаз.
Индивидуальная работа.(слайд 10)
№292.
Все виды работ на уроке оценивать по следующей схеме:
Дополнительно. (Слайд11) 1.Найдите корни квадратного трехчлена (x-4)²+(4y-12)². 2.Найдите значения параметра a, при каждом из которых квадратный трехчлен x²+4x+2ax+8a+1 имеет одно решение. a)найдите значение параметра а, при котором квадратный трехчлен x²-6x+2ax+4a не имеет решения; b)найдите корни квадратного трехчлена (2x-6)²+(3y-12)² |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Конец урока 2 мин.
1 мин. |
Домашнее задание. По учебнику А. Шыныбекова Алгебра 8 класс: № 326
В конце урока рефлексия: - что узнал, чему научился - что осталось непонятным - над чем необходимо работать |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? |
Оценивание – как Вы планируете проверить уровень усвоения материала учащимися? |
Здоровье и соблюдение техники безопасности |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Учащимся будет предоставлен набор критериев успеха для оценивания правильности выполнения работы. |
В процессе работы над решением проблемной ситуации учащимися демонстрируется креативный и критический подход |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Рефлексия по уроку Были ли цели урока/цели обучения реалистичными? Все ли учащиеся достигли ЦО? Если нет, то почему? Правильно ли проведена дифференциация на уроке? Выдержаны ли были временные этапы урока? Какие отступления были от плана урока и почему? |
Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Общая оценка
Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)? 1:
2: Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)? 1:
2: Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
Приложение 1
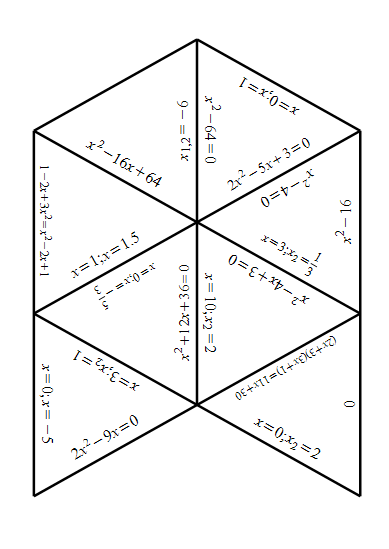
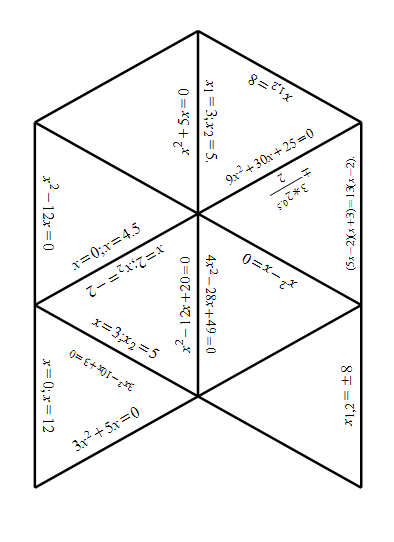
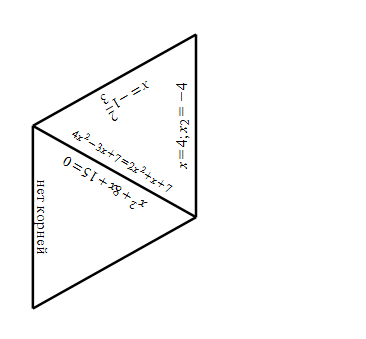
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.