2.24 Треугольники и четырехугольники на клетчатой бумаге.

Треугольники и четырехугольники на клетчатой бумаге.

Повторяем теорию

Высота треугольника ‒ это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.

Высота параллелограмма — это перпендикуляр, опущенный из любой точки одной стороны параллелограмма на прямую, содержащую противоположную сторону.

Высота трапеции – это перпендикуляр, опущенный из любой точки одного основания к другому основанию

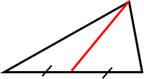Медиана треугольника ‒ отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

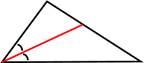Биссектриса треугольника ‒ отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны

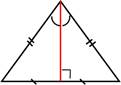В равнобедренном треугольнике медиана, проведённая к основанию, одновременно является биссектрисой и высотой.

Свойства прямоугольного треугольника.

1)  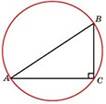 Радиус окружности, описанной вокруг прямоугольного треугольника, равен половине гипотенузы: R= 1 АВ

2

(Центр окружности, описанной около прямоугольного треугольника — середина гипотенузы).

2)   В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна половине гипотенузы.

3)   В равнобедренном прямоугольном треугольнике биссектриса, высота, медиана, проведённая к гипотенузе, равна половине гипотенузы.

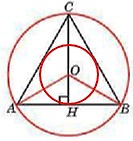В равностороннем треугольнике центры вписанной и описанной окружностей совпадают.

Центр равностороннего треугольника – точка пересечения медиан, биссектрис и высот, делит эти отрезки в отношении 2:1, считая от вершины треугольника.

Радиус вписанной окружности r= ОН= 1 СН,

3

радиус описанной окружности R= ОС =

1   СН.

3

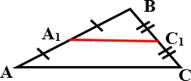Средняя линия треугольника ‒ отрезок, соединяющий середины двух сторон треугольника.

Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна её половине.

А₁С₁ || АС, А₁ С₁ =

1 АС.

2

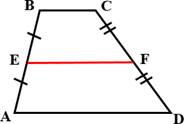Средняя линия трапеции ‒ отрезок, соединяющий середины боковых сторон этой трапеции.

Средняя линия параллельна основаниям и равна их полусумме.

BC + AD

EF || AD || BC,                 ЕF =       2       .

Проверяем себя.

Т1. Вставьте пропущенное слово:

а) Высота треугольника ‒ это                                          , проведённый из вершины треугольника к прямой, содержащей противоположную сторону.

б)                                             треугольника  ‒   отрезок,  соединяющий  вершину

треугольника с серединой противолежащей стороны.

в)                  Биссектриса     треугольника     ‒                            

треугольника,

соединяющий вершину треугольника с точкой противоположной стороны.

г)                                      –   точка   пересечения   медиан,   биссектрис   и   высот

равностороннего треугольника.

Ответ: а) перпендикуляр; б) медиана; в) отрезок биссектрисы угла; г) центр равностороннего треугольника.

Т2. Выберите верное утверждение.

а) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.

б)                 Любая    медиана    равнобедренного    треугольника    является    его биссектрисой.

в) У равнобедренного треугольника есть центр симметрии.

Ответ: а).

Т3. Выберите верное утверждение

1)     Средняя линия треугольника ‒ это отрезок, соединяющий боковые стороны.

2)  Средняя линия трапеции равна половине её основания.

3)      Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне.

Ответ: 3.

Решаем задачи.

1.     а) Фигуры изображены на клетчатой бумаге с размером клетки 1×1.

Ответ: 1) 5; 2) 3; 3) 4.

б) Фигуры изображены на клетчатой бумаге с размером клетки 1×1.

Ответ: 1) 5; 2) 3; 3) 3.

в) Фигуры изображены на клетчатой бумаге с размером клетки 1×1.

Ответ:1) 4; 2) 3; 3) 6.

2.     а)  На  клетчатой           бумаге   с   размером   клетки   1×1   изображён равнобедренный прямоугольный треугольник.

Ответ: 1) 3,5; 2) 4,5; 3) 1,5.

б) На клетчатой бумаге с размером клетки 1×1 изображён равнобедренный прямоугольный треугольник.

Ответ: 1) 2,5; 2) 2,5; 3) 3,5.

в) На клетчатой бумаге с размером клетки 1×1 изображён равнобедренный прямоугольный треугольник.

Ответ: 1) 1,5; 2) 3,5; 3) 2,5.

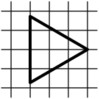
3.  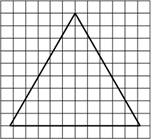                а)   На   клетчатой   бумаге   с   размером   клетки   1×1   изображён равносторонний треугольник.

Ответ: 1) 6; 2) 1.

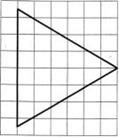
б) На клетчатой бумаге с размером клетки 1×1 изображён равносторонний треугольник.

Ответ: 1) 4; 2) 3.

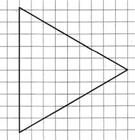
в) На клетчатой бумаге с размером клетки 1×1 изображён равносторонний треугольник.

Ответ: 1) 10; 2) 2.

4.                  а)   На   клетчатой   бумаге   с   размером   клетки   1×1   изображён параллелограмм.

Ответ: 1) 9; 2) 8; 3) 3; 4) 10.

б) На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм.

Ответ: 1) 8; 2) 8; 3) 5; 4) 5.

в) На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм.

Ответ: 1) 4; 2) 4; 3) 6; 4) 13.

5.            а) Фигуры изображены на клетчатой бумаге с размером клетки 1×1.

Ответ: 1) 3; 2) 3; 3) 4.

б) Фигуры изображены на клетчатой бумаге с размером клетки 1×1.

Ответ: 1) 2; 2) 7; 3) 4.

в) Фигуры изображены на клетчатой бумаге с размером клетки 1×1.

Ответ: 1) 2; 2) 3; 3) 5.

6.            а) Фигуры изображены на клетчатой бумаге с размером клетки 1×1.

Ответ: 1) 3; 2) 2; 3) 5.

б) Фигуры изображены на клетчатой бумаге с размером клетки 1×1.

Ответ: 1) 6, 2) 5,5; 3) 2,5.

в) Фигуры изображены на клетчатой бумаге с размером клетки 1×1.

Ответ: 1) 2; 2) 3; 3) 8,5.

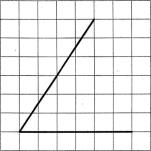
7.  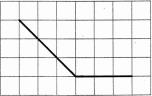            а) На клетчатой бумаге с размером клетки 1×1 изображены углы. Найдите тангенсы этих углов.

Ответ: 1) 1,5; 2) ‒1.

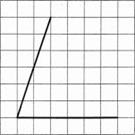
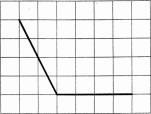б) На клетчатой бумаге с размером клетки 1×1 изображены углы. Найдите тангенсы этих углов.

Ответ: 1) 3; 2) ‒2.

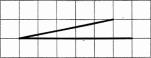
в) На клетчатой бумаге с размером клетки 1×1 изображены углы. Найдите тангенсы этих углов.

Ответ: 1) 0,2; 2) ‒0,25.

Дополнительные задачи.

1. 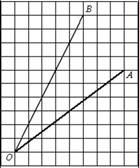 Найти тангенс угла АОВ

Ответ: 0,5.

2. 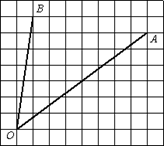 Найти тангенс угла АОВ:

Ответ: 1