3_Математика_7класс_степень_Стандартный_вид_числа_Приложение_к_уроку_01

Теоретический материал

СТАНДАРТНЫЙ ВИД ЧИСЛА

В физике, астрономии, технике часто приходится иметь дело с величинами, значения которых выражаются очень большими или очень малыми числами.

Например, масса Земли равна 5 980 000 000 000 000 000 000 т, а масса одного атома железа 0, 000 000 000 000 000 000 000 0927 г. Такие числа не только трудно читать, но о них даже трудно получить явное представление, с ними неудобно выполнять вычисления. Поэтому очень большие или очень маленькие числа принято записывать в виде , где а – число, заключенное между 1 и 10, а п – целое число. Такую запись называют стандартным видом числа.

Стандартным видом числа х называют запись этого числа в виде , где  и . Число а называют значащей частью числа х, а целое число п называют порядком этого числа.

Масса Земли в стандартном виде запишется так:  т, а масса одного атома железа – в виде  г.

Порядок числа позволяет оценить, насколько велико или мала число. Он дает возможность сравнивать большие и малые числа.

Например, известно, что масса Юпитера равна  т. Сравнивая ее с массой Земли, мы можем сказать, что она на 3 порядка больше массы земли.

Известно, что сила звука (громкость) оказывает на человека как положительное, так и отрицательное воздействие. В акустике силу звука измеряют в единицах Вт/см². Сравним шорох листьев в лесу в тихую погоду (он оценивается как  Вт/см²) и шум на оживленной городской улице ( Вт/см²). Из этого сравнения видно, что шум на городской улице на 5 порядков, т.е. в 100 000 раз, больше шороха листьев в лесу. Какой из этих «шумов» благоприятнее для человека, нетрудно сделать вывод. Заметим, что сила звука, равная  Вт/см², вызывает у человека болевое ощущение.

Алгоритм перехода от обычной десятичной дроби к стандартному виду очень прост. Но перед тем как его использовать, обязательно повторите, что такое значащая часть числа 

1.             Выписать значащую часть исходного числа и поставить после первой значащей цифры десятичную точку;

2.             Найти образовавшийся сдвиг, т.е. на сколько разрядов сместилась десятичная точка по сравнению с исходной дробью. Пусть это будет число k;

3.             Сравнить значащую часть, которую мы выписали на первом шаге, с исходным числом. Если значащая часть (с учетом десятичной точки) меньше исходного числа, дописать множитель 10^k. Если больше — дописать множитель 10^−k. Это выражение и будет стандартным видом.

Рассмотрим примеры записи числа в стандартном виде.

Пример 1. Представим в стандартном виде число  х = 63 800 000.

Число х должно иметь вид . Поставив в числе х запятую после цифры 6 (6,3800000), мы тем самым отделили запятой 7 цифр справа, т.е. уменьшили число х в 10⁷ раз. Поэтому х больше 6,38 в 10⁷ раз. Значит,  х = .

Пример 2. Запишем в стандартном виде число  х = 0,0000327.

Число х должно иметь вид , т.е. в значащей части числа до запятой должна быть одна цифра, отличная от нуля. Переставив запятую на 5 знаков вправо, мы увеличили число х в 10⁵ раз. Поэтому х меньше 3,27 в 10⁵ раз. Значит,

х = 3,27 :  10⁵  = .

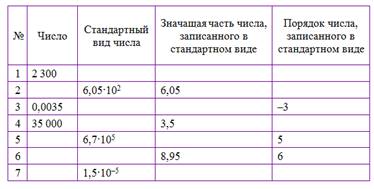
Заполните таблицу:

Выберите букву, соответствующую записи числа в стандартном виде:

А) Ниже приведены два примера, в которых объясняется, как число записать в стандартном виде. Один из вас должен изучить пример 1, а другой – пример 2, обратите внимание на то, какие слова и фразы использованы. Затем объясните свои примеры друг другу.

Пример 1. Представьте число 4209 в стандартном виде. Назовите значащую часть и порядок числа.

Так как значащая часть числа, записанного в стандартном виде, меньше десяти, но не меньше одного, то число 4209 должно иметь вид . Мы переставили запятую на 3 знака влево, значит число 4209 в 1000 раз больше числа 4,209. Тогда,

4209 = .

Значащая часть числа равна 4,209, а порядок равен 3.

Пример 2. Запишите число 0,00007 в стандартном виде.

Данное число в стандартном виде должно иметь вид , так как . Мы переставили запятую на 5 знаков вправо, поэтому число 0,00007 увеличилось в  раз, следовательно,

0,00007 = .

Значащая часть числа равна 7, а порядок равен -5.

В) Запишите числа 4 800 000 и 0,0156 в стандартном виде и сверьте ваши результаты.

Дополнительные задачи:

1. Площадь территории Испании составляет 506 тыс. км². Как эта величина записывается в стандартном виде?

2. Площадь территории некоторой страны составляет 342 тыс км². Как эта величина записывается в стандартном виде?

3. Площадь территории некоторой страны составляет 2 млн. км². Как эта величина записывается в стандартном виде?

4. Общее количество биомассы Мирового океана оценивается в 35 миллиардов тонн. Как эта величина записывается в стандартном виде?

5. Найдите десятичную дробь, равную: 1,65×10³; 1,65×10^-8; 1,65×10^-5.

6. Запишите число в стандартном виде:

7. Найдите числа, записанные в стандартном виде и по соответствующим буквам составьте название числа. Узнайте историю этого термина.

Скачано с www.znanio.ru