6. Методические рек к проведению урока. Вариант 1

Методические рекомендации

       Начните урок с организационного момента, приветствие, отметка отсутствующих, проверка готовности учащихся к урок. Совместно с учащимися определите цели урока, критерии оценивании, обсудите ход урока. Проведите выборочную проверку домашнего задания.

Для подготовки учащихся к усвоению нового материала предложите ответить на вопросы:

Мы закончили изучение очень важного раздела в математике.

- какого?

Умеем выполнять все действия с натуральными числами, десятичными и обыкновенными дробями?

Сколько арифметических действий вы знаете?

Проведем блиц –опрос:

- это действие можно записать не используя ни одного из арифметических знаков

- это действие можно заменить другим действием

Вы догадались? Задайте вопросы друг другу об этом действии.

- какое это действие?

- назовите компоненты этого действия

- как можно его записать не используя арифметических знаков?

- каким действием можно заменить его?

-как называется результат деления?

Для того, чтобы учащиеся узнали тему урока предложите учащимся задание.

Теоретический материал: Объяснение нового материала.

На данном уроке вводится понятие отношения двух неравных нулю чисел a и b, отношения величин и соответствующая терминология: члены отношения, однородные величины. Подчеркнём, что отношением двух неравных нулю чисел a и b называют как выражение a : b, так и его значение.

Показывается, что некоторые известные величины являются отношениями других величин (скорость, плотность вещества, цена). Здесь же сформулировано свойство отношения.

Учащиеся должны понимать, что отношение величин одного наименования (длин, скоростей и т. д., выраженных одинаковыми единицами измерения), есть число, а отношение величин разных наименований (пути и времени, стоимости товара и его количества и т.д.) есть новая величин.

Для закрепления полученных знании объедините учащихся в пары. Предложите каждой паре заполнить пустые клетки таблицы

Пары обмениваются решениями и осуществляют взаимопроверку.

      Предложите учащимся проблемную ситуацию. На доске изображены два отрезка АВ и СD. Пусть АВ = 15 см и СD = 5 см. Сравните длины отрезков АВ и СD. Определите, во сколько раз длина одного больше/меньше длины другого. Предложите учащимся записать действие, описывающее ответ на вопрос.

Сформулируйте определение: «Отношением двух величин называют ... ». При реализации данной деятельности используется принцип дифференциации «Проблемное обучение», которое позволяет учащимся развить навыки самостоятельного формирования новых знаний и их глубокого понимания.

Предложите учащимся индивидуальное задание.

Найдите отношение чисел

Предложите учащимся математический диктант.

Учащиеся записывают в тетрадях ответы. Один ученик работает у доски. Затем фронтально проверяют правильность выполнения заданий.

На данном этапе урока у учащихся развивается ценность: умение слушать и слышать друга и учителя, уважительное отношение друг другу.

Математический диктант

-Найдите отношение 23 к 8

-10 к 0,1

-0,2 к 0,3

-запишите в виде отношения: число a в 5 раз больше числа b

-запишите в виде отношения: число с в 3 раза меньше числа n

-Какую часть составляет число 7 от числа 9?

-Верно ли высказывание: отношение двух чисел увеличится вдвое, если увеличить в два раза каждое из чисел?

Приведите пример.

-Можно ли определенно назвать два числа, если известно, что их отношение равно 2?

Приведите пример.

Работа в парах. Взаимное обучение. Прикладные задачи.

Создадим пары с разным уровнем обучаемости. Предложим учащимся процесс взаимного обучения при решении практических задач: объяснять решение задачи своему напарнику при возникновении вопроса по той или иной задаче, т.е. ученики выполняют задания индивидуально, но имеют возможность обсудить непонятные вопросы с напарником.

Пример 1. Найдите отношение величин:

1) ; 2) .

Отношение однородных величин показывает во сколько раз одна величина больше другой.

Отношение величин разных наименований (пути и времени , стоимости товара и его количества , массы тела и его объема  и т.д.) есть новая величина.

Отношение величин в математике.

Отношение пути (км) к времени (ч) есть новая величина – скорость, выраженная в единицах скорости (км/ч)

 .

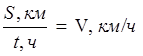Пример 2. Найдите отношение пути 16 км к времени 8 ч:

.

Отношение величин в математике.

Отношение стоимости товара (р.) к его массе (кг) есть новая величина – цена, выраженная в единицах цены (р./кг)

.

Знаменатель в единицах цены обычно не пишут, а пишут и говорят «цена 1 кг товара 50 р.».

Пример 3. Найдите отношение стоимости товара 24 р. к его массе 8 кг: .

Отношение величин в физике.

Отношение массы тела (кг) к его объему (м³) есть новая величина –плотность вещества, выраженная в единицах плотности (кг/м³).

.

Пример 4. Найдите отношение массы бруса 120 кг к его объёму 40 м³

.

Отношение величин в химии.

Отношение массы вещества (например, соли) (кг) к объему раствора (м³) есть новая величина – концентрация раствора, выраженная в единицах концентрации (кг/м³).

Пример 5. Найдите отношение массы соли (82 кг) к объёму раствора (42 м³): .

Предложите учащимся придумать свои примеры на отношения двух чисел.

Ресурсы:

http://festival.1september.ru/articles/413794/

http://free.megacampus.ru/xbookM0005/index.html?go=part–004*page.htm

ttp://math–prosto.ru/?page=pages/ratio_of_numbers/ratio_of_numbers.php

http://www.for6cl.uznateshe.ru/chto–takoe–otnoshenie–chisel/

http://znaika.ru/catalog/6–klass/matematika/Otnoshenie–dvukh–chisel

Скачано с www.znanio.ru