7Motion of a body dropped at an angle to the horizon

Theoretical material

Projectile motion is the motion of an object thrown or projected into the air, subject to only the acceleration of gravity. The object is called a projectile, and its path is called its trajectory. The motion of falling objects, as covered in Problem-Solving Basics for One-Dimensional Kinematics, is a simple one-dimensional type of projectile motion in which there is no horizontal movement. In this section, we consider two-dimensional projectile motion, such as that of a football or other object for which air resistance is negligible.

The most important fact to remember here is that motions along perpendicular axes are independent and thus can be analyzed separately. This fact was discussed in Kinematics in Two Dimensions: An Introduction, where vertical and horizontal motions were seen to be independent. The key to analyzing two-dimensional projectile motion is to break it into two motions, one along the horizontal axis and the other along the vertical. (This choice of axes is the most sensible, because acceleration due to gravity is vertical—thus, there will be no acceleration along the horizontal axis when air resistance is negligible.) As is customary, we call the horizontal axis the x-axis and the vertical axis the y-axis. Figure 1 illustrates the notation for displacement, where s is defined to be the total displacement and x and y are its components along the horizontal and vertical axes, respectively. The magnitudes of these vectors are s, x, and y. (Note that in the last section we used the notation A to represent a vector with components Ax and Ay. If we continued this format, we would call displacement s with components sx and sy. However, to simplify the notation, we will simply represent the component vectors as x and y.)

Of course, to describe motion we must deal with velocity and acceleration, as well as with displacement. We must find their components along the x– and y-axes, too. We will assume all forces except gravity (such as air resistance and friction, for example) are negligible. The components of acceleration are then very simple: ay = –g = –9.80 m/s². (Note that this definition assumes that the upwards direction is defined as the positive direction. If you arrange the coordinate system instead such that the downwards direction is positive, then acceleration due to gravity takes a positive value.) Because gravity is vertical, ax=0. Both accelerations are constant, so the kinematic equations can be used.

Given these assumptions, the following steps are then used to analyze projectile motion:

Step 1. Resolve or break the motion into horizontal and vertical components along the x- and y-axes. These axes are perpendicular, so A_x = A cos θ and Ay = A sin θ are used. The magnitude of the components of displacement s along these axes are x and y. The magnitudes of the components of the velocity v are V_x = V cos θ and V_y = v sin θ where v is the magnitude of the velocity and θ is its direction, as shown in 2. Initial values are denoted with a subscript 0, as usual.

Step 2.Treat the motion as two independent one-dimensional motions, one horizontal and the other vertical. The kinematic equations for horizontal and vertical motion take the following forms:

Step 3. Solve for the unknowns in the two separate motions—one horizontal and one vertical. Note that the only common variable between the motions is time t. The problem solving procedures here are the same as for one-dimensional kinematics and are illustrated in the solved examples below.

Step 4. Recombine the two motions to find the total displacement s and velocity v. Because the x – and y -motions are perpendicular, we determine these vectors by using the techniques outlined in the Vector Addition and Subtraction: Analytical Methods and employing A=√Ax2+Ay2A=Ax2+Ay2 and θ = tan⁻¹ (Ay/Ax) in the following form, where θ is the direction of the displacement s and θv is the direction of the velocity v:

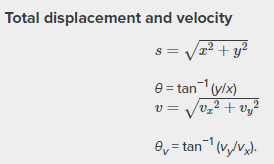
Answers to the solving problems from didactic material #1

1 a) 25 m/s, 19.6 m/s down  b) 38.6 m/s @ 49.6° down  c) 87 m @ 30.5° down  

2 a) 7.1 s  b) 12 m/s  

3. 31 m

4. a) 32.5 m/s, 56 m/s  b) 130 m  

5. a) 123 m  b) 600 m  

6. 660 m/s  

7. a) 5.1 s  b) 80 m  c) 38 m  d) 40.3 m/s @ 79.3° down  

8. a) 8.1 s  b) 23°

9. a) 7.1 s  b) 122 m  c) 62 m/s @ 74° down

Additional differentiated problems

Problem# 1
For Δd_y = 0 and for any given v_o find θ so that the range (Δd_x) is maximum.

Problem # 2
Find the maximum height (h) and range for v_o = 10 m/s, θ = 30°, and Δd_y = -10 m. What is the flight time?

Problem # 3
Find the maximum height and range for v_o = 10 m/s, θ = 30°, and Δd_y = 1 m. The displacement Δd_y corresponds to the stage of the projectile flight where it is moving downward. What is the flight time?

Problem # 4
Find Δd_y for v_o = 10 m/s, θ = 30°, and Δd_x = 15 m. What is the flight time?

Problem # 5
Find the maximum height and range for v_o = 10 m/s, and θ = 90°.

Problem # 6
Find the maximum height and range for v_o = 10 m/s, θ = 0, and Δd_y = -5 m.

Problem # 7
Find the maximum height and range for v_o = 10 m/s, θ = 30°, and Δd_y = -10 m. Account for air resistance, with drag coefficient equal to 0.47, projected frontal area equal to 0.01 m², density of air equal to 1.2 kg/m³, and mass of projectile equal to 0.1 kg. Compare this to the answer in problem 2.

Problem # 8


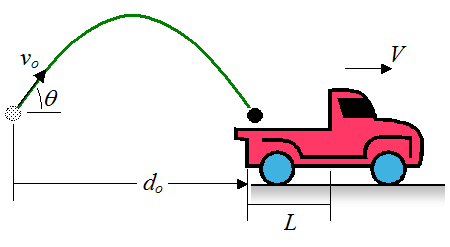
A ball is kicked at an angle θ = 45°. It is intended that the ball lands in the back of a moving truck which has a trunk of length L = 2.5 m. If the initial horizontal distance from the back of the truck to the ball, at the instant of the kick, is d_o = 5 m, and the truck moves directly away from the ball at velocity V = 9 m/s (as shown), what is the maximum and minimum velocity v_o so that the ball lands in the trunk. Assume that the initial height of the ball is equal to the height of the ball at the instant it begins to enter the trunk.

Скачано с www.znanio.ru