АГРЕГУВАННЯ ГАЛУЗЕЙ У МІЖАЛУЗЕВОМУ БАЛАНСІ Опис методів лабораторної роботи

АГРЕГУВАННЯ ГАЛУЗЕЙ У МІЖАЛУЗЕВОМУ БАЛАНСІ

Опис методів лабораторної роботи

          У економіко-математичному моделюванні актуальною є задача  агрегування галузей. Агрегування дозволяє перетворити складну модель у просту або зменшити розмірність моделі. Це дозволяє мінімізувати матеріальні, фінансові, трудові та інші ресурси.

         Початковими даними в моделі агрегування виступає міжгалузевий баланс виробництва та розподілу продукції (таблиця 5.1), який містить шахову таблицю, вектори кінцевої, валової та умовно-чистої продукції.  

          У міжгалузевому балансі виробництва та розподілу продукції розглядаються n галузей. Необхідно побудувати новий     міжгалузевий баланс на основі об’єднання  деяких, наперед заданих галузей та визначити за новою моделлю матрицю коефіцієнтів прямих матеріальних витрат. Нехай це будуть k, l та r галузі, (k, l, r)=1,....n. Номер нової галузі позначимо m. Сформульовану задачу можна розв’язати аналітичним та матричним методами.

         У аналітичному методі для визначення міжгалузевих потоків нової галузі використовуються формули

                                                     (6.1)

                                                    (6.2)

                                   (6.3)

Кількість валової  та кінцевої продукції нової галузі дорівнює

                                                                                           (6.4)

           Коефіцієнти прямих матеріальних витрат галузі m обчислюються за формулами

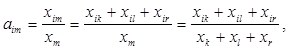                                                              (6.5)

                                                               (6.6)

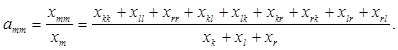                                       (6.7)

Так як у нових міжгалузевому балансі та матриці коефіцієнтів прямих матеріальних витрат зменшилась кількість рядків та стовпців, то номери галузей необхідно скорегувати.

          У матричному методі агрегування виконуються операції над матрицями. Розглянемо цей метод для чотирьох галузей економіки. Необхідно визначити матрицю коефіцієнтів прямих матеріальних витрат, якщо об’єднаються друга та третя галузі.

          Нова матриця коефіцієнтів прямих матеріальних витрат  А* обчислюється за формулою

                                            А*=І*АВ*,                                                              (6.8)

 де  І* -  скорегована одинична матриця, А – початкова матриця коефіцієнтів прямих матеріальних витрат, В* - скорегована матриця вагових коефіцієнтів.

         Матрицю І* можна одержати в результаті складання відповідних елементів другого та третього рядків одиничної матриці

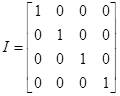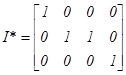                         ,             .                               (6.9)

         Матрицю В* отримують із матриці вагових коефіцієнтів В у результаті складання відповідних елементів другого та третього стовпців

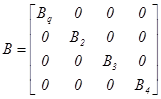
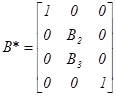                  ,             .                            (6.10)

Вагові коефіцієнти визначаються таким чином                                            

                                                    ,                                                            (6.11)

                                                ,                                                       (6.12)

                                                 ,                                                      (6.13)

                                                     ,                                                           (6.14)

           Правильно виконані розрахунки дозволяють одержати однакові результати на основі використання як аналітичного, так і матричного методів.