алгебра

Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год

Зачетная работа по теме Уравнения и неравенства. Системы уравнений и неравенств - Уравнения и неравенства. Системы уравнений и неравенств

Цель: проверить знания учащихся по вариантам одинаковой сложности.

Ход уроков

I. Сообщение темы и цели уроков

II. Варианты зачетной работы

Вариант 1

А

1. Решите уравнение:

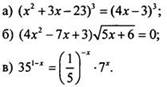
2. Решите систему уравнений:

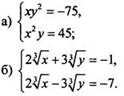
3. Решите неравенство: 

4. Решите уравнение: 

В

5. Дана функция f(x) = 4х² - х. Решите уравнение f(f(х)) = 33.

6. Решите уравнение: 

7. Решите систему уравнений: 

8. Решите неравенство: 

C

9. Решите уравнение: 

10. Найдите все пары (х; у) положительных чисел х и у, которые являются решениями системы уравнений: 

11. Найдите значения а, при которых произведение действительных корней уравнения  принимает наименьшее и наибольшее значения. Найдите также эти значения.

Вариант 2

А

1. Решите уравнение:

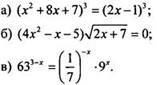
2. Решите систему уравнений:

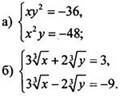
3. Решите неравенство: 

4. Решите уравнение: 

В

5. Дана функция f(х) = 5x² -х. Решите уравнение f(f(x)) = 76.

6. Решите уравнение: 

7. Решите систему уравнений: 

8. Решите неравенство: 

C

9. Решите уравнение: 

10. Найдите все пары (х; у) положительных чисел х и у, которые являются решениями системы уравнений: 

11. Найдите значения a, при которых произведение действительных корней уравнения  принимает наименьшее и наибольшее значения. Найдите также эти значения.

III. Ответы и решения

Вариант 1

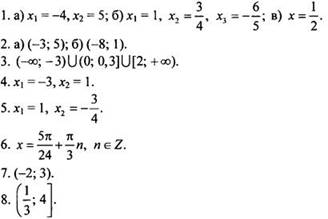
9. ОДЗ уравнения задается условием sin х ≠ 0. Запишем уравнение в виде:  или  или  Такое уравнение является однородным. Поэтому разделим все члены уравнения на sin²x и получим: 2ctgx + 13ctgx + 15 = 0. Решения уравнения: ctgx = -5 (тогда ) и ctgx = -3/2 (откуда ).

Ответ: 

10. Прологарифмируем каждое уравнение по основанию 2 и запишем систему в виде  Разделим первое уравнение на второе:  или 3у - 11 = 2у - 6, откуда у = 5. Подставим эту величину, например, во второе уравнение: 2log₂x = 2, тогда log₂x = 1 и x = 2. Система имеет единственное решение (2; 5).

Ответ: (2; 5).

11. ОДЗ уравнения задается неравенством 14a - 4a² - 10 ≥ 0 или 2a² - 7a + 5 ≤ 0, откуда а ∈ [1; 5/2]. Так как данное квадратное уравнение имеет корни, то его дискриминант D = 14а - 4a² – 10 - 4(-2а² + 8а - 7) = 4а² - 18а + 18 ≥ 0. Решение этого неравенства  С учетом ОДЗ находим диапазон изменения параметра а ∈ [1; 3/2]. По теореме Виета произведение корней данного квадратного уравнения у = -2а² + 8а - 7. Функция у(а) имеет максимум при а = 2. На отрезке а ∈ [1; 3/2] функция у(а) возрастает. Поэтому при а = 1 функция принимает наименьшее значение  при а = 3/2 - наибольшее значение 

Ответ: наименьшее значение (-1) при а = 1 и наибольшее значение 0,5 при а = 1,5.

Вариант 2

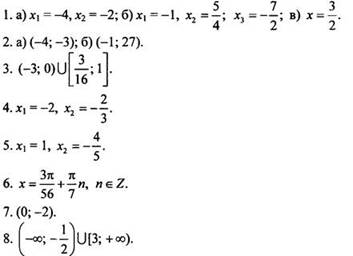
9. ОДЗ уравнения задается условием cos х ≠ 0. Запишем уравнение в виде 49cos² х + 11sin x cos x = 4, или 0 = 4sin² x + 4cos² x- 11sin x cos x - 49cos² x, или 0 = 4sin² x - 11sin x cos x - 45cos²x. Такое уравнение является однородным. Поэтому разделим все члены уравнения на cos² x и получим: 0 = 4tg² x - 11tg x - 45. Решения уравнения: tg x = 5 (тогда х = arctg5 + πn, n ∈ Z) и tgx= -9/4 (откуда х = arctg(-9/4) + πn).

Ответ: 

10. Прологарифмируем каждое уравнение по основанию 2 и запишем систему в виде  Разделим первое уравнение на второе:  или 16у - 4 = 3у + 9, откуда у = 1. Подставим эту величину, например, во второе уравнение: 4log₂x = 4, тогда log₂x = 1 и х = 2. Система имеет единственное решение (2; 1).

Ответ: (2; 1).

11. ОДЗ уравнения задается неравенством a² + a - 2 ≥ 0, откуда a ∈ (-∞; -2] U [1; +∞). Так как данное квадратное уравнение имеет корни, то его дискриминант D = a² + а – 2 - (2а² - 4) = -а²+ а + 2 ≥ 0. Решение этого неравенства а ∈ [-1; 2]. С учетом ОДЗ находим диапазон изменения параметра а ∈ [1; 2]. По теореме Виета произведение корней данного квадратного уравнения у = 2а² - 4. Функция у(а) имеет минимум при а = 0. На отрезке а ∈ [1; 2] функция y(a) возрастает. Поэтому при а = 1 функция принимает наименьшее значение  при а = 2 - наибольшее значение 

Ответ: наименьшее значение (-2) при а = 1 и наибольшее значение 4 при а = 2.