Конспект урока по алгебре: «Уравнения (9 класс)» (

Тема урока «Системы линейных уравнений »

Тип урока: урок изучения нового материала

Цель урока: познакомить с определением системы уравнений с двумя переменными, решением системы уравнений с двумя переменными

образовательная:

- ввести понятие системы уравнений, решения системы;

- сформировать умение находить количество решений, не решая систему;

развивающая:

- развитие культуры устной и письменной речи учащихся;

- развитие мышления учащихся через умение анализировать и выделять

главное;

воспитательная:

- воспитание аккуратности.

Формы работы: фронтальная, индивидуальная

Ход урока

1. Организационный момент

13 лет – время, когда всерьёз можно задуматься над вопросом бедующей профессии. А хорошее решение может быть принято только на основе знаний. Усердное изучение математики, систематические знания учат правильно рассуждать, принимать обоснованные решения, защищать и отстаивать своё мнение, развивать память и воображение. Значит занятие математикой – это первый шаг к будущей профессии. Давайте продолжим делать этот шаг.

2. Устная работаРабота по карточкам (задания из сборников для подготовки к ОГЭ)

2. Актуализация опорных знаний

Фронтальный опрос:

1. Какое уравнение называется линейным уравнением с двумя переменными?

2. Что является графиком уравнения?

3. Что является решением уравнения?

4. Как найти решения уравнения?

5. Как узнать будет ли пара (1;1) решением уравнения 2x + y = 5?

6. Найти три решения уравнения?

3. Объяснение нового материала

Ставит проблему: х + y = 3 и y = х - 5

Как найти решение, которое будет являться решением и одного и другого уравнения?

Чтобы найти общее решение этих уравнений надо найти такие значения переменных, которые обращают в верное равенство каждое из уравнений. В таких случаях говорят, что требуется решить систему уравнений.

Открываем тетради, записываем число, тему урока: ««Системы линейных уравнений с двумя переменными».

Систему уравнений принято записывать с помощью фигурной скобки:

Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство.

Проверить является ли пара (1;2), (4;-1) решением системы (образец выполнения показывает на доске).

Как решать системы линейных уравнений вы узнаете на последующих уроках. А сейчас вы узнаете как, не решая систему уравнений, определить, сколько решений она имеет.

Рассмотрим систему:

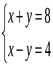
Выразим из каждого уравнения у через х:

Уравнения задаются линейными функциями. Видим, что угловые коэффициенты прямых, являющихся графиками этих функций, различны. Значит прямые пересекаются и система имеет единственное решение.

Правило:

1) если угловые коэффициенты прямых, являющихся графиками функций, различны, то система имеет единственное решение.

2) если угловые коэффициенты прямых, являющихся графиками функций, одинаковы, а b различны, то система не имеет решений.

3) если уравнения имеют одинаковый вид, то система имеет бесконечно много решений.

4. Закрепление

Работа по учебнику: №1056, №1063

5. Первичное закрепление нового материала

1. Выяснить, сколько решений имеет система.

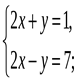
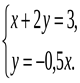
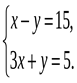
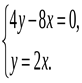
2. Является ли решением системы уравнений

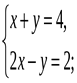
пара (3;1)

пара (2;2)

6. Постановка домашнего задания и его комментарий

п.42 (определение и примеры), №1057, №1064

7. Подведение итогов урока

1.      Какие новые понятия узнали на уроке?

2.      Что нового узнали на уроке.