Алгебра логики и логические основы компьютера

Что такое алгебра логики?

Алгебра логики (булева алгебра) – это раздел математики, возникший в XIX веке благодаря усилиям английского математика Дж. Буля. Поначалу булева алгебра не имела никакого практического значения. Однако уже в XX веке ее положения нашли применение в описании функционирования и разработке различных электронных схем. Законы и аппарат алгебры логики стал использоваться при проектировании различных частей компьютеров (память, процессор). Хотя это не единственная сфера применения данной науки.

Что же собой представляет алгебра логики? Во-первых, она изучает методы установления истинности или ложности сложных логических высказываний с помощью алгебраических методов. Во-вторых, булева алгебра делает это таким образом, что сложное логическое высказывание описывается функцией, результатом вычисления которой может быть либо истина, либо ложь (1, либо 0). При этом аргументы функции (простые высказывания) также могут иметь только два значения: 0, либо 1.

Что такое простое логическое высказывание? Это фразы типа «два больше одного», «5.8 является целым числом». В первом случае мы имеем истину, а во втором ложь. Алгебра логики не касается сути этих высказываний. Если кто-то решит, что высказывание «Земля квадратная» истинно, то алгебра логики это примет как факт. Дело в том, что булева алгебра занимается вычислениями результата сложных логических высказываний на основе заранее известных значений простых высказываний.

Логические операции. Дизъюнкция, конъюнкция и отрицание

Так как же связываются между собой простые логические высказывания, образуя сложные? В естественном языке мы используем различные союзы и другие части речи. Например, «и», «или», «либо», «не», «если», «то», «тогда». Пример сложных высказываний: «у него есть знания и навыки», «она приедет во вторник, либо в среду», «я буду играть тогда, когда сделаю уроки», «5 не равно 6». Как мы решаем, что нам сказали правду или нет? Как-то логически, даже где-то неосознанно, исходя из предыдущего жизненного опыта, мы понимает, что правда при союзе «и» наступает в случае правдивости обоих простых высказываний. Стоит одному стать ложью и все сложное высказывание будет лживо. А вот, при связке «либо» должно быть правдой только одно простое высказывание, и тогда все выражение станет истинным.

Булева алгебра переложила этот жизненный опыт на аппарат математики, формализовала его, ввела жесткие правила получения однозначного результата. Союзы стали называться здесь логическими операторами.

Алгебра логики предусматривает множество логических операций. Однако три из них заслуживают особого внимания, т.к. с их помощью можно описать все остальные, и, следовательно, использовать меньше разнообразных устройств при конструировании схем. Такими операциями являются конъюнкция (И), дизъюнкция (ИЛИ) иотрицание (НЕ). Часто конъюнкцию обозначают &, дизъюнкцию - ||, а отрицание - чертой над переменной, обозначающей высказывание.

При конъюнкции истина сложного выражения возникает лишь в случае истинности всех простых выражений, из которых состоит сложное. Во всех остальных случаях сложное выражение будет ложно.

При дизъюнкции истина сложного выражения наступает при истинности хотя бы одного входящего в него простого выражения или двух сразу. Бывает, что сложное выражение состоит более, чем из двух простых. В этом случае достаточно, чтобы одно простое было истинным и тогда все высказывание будет истинным.

Отрицание – это унарная операция, т.к выполняется по отношению к одному простому выражению или по отношению к результату сложного. В результате отрицания получается новое высказывание, противоположное исходному.

Таблицы истинности

Логические операции удобно описывать так называемыми таблицами истинности, в которых отражают результаты вычислений сложных высказываний при различных значениях исходных простых высказываний. Простые высказывания обозначаются переменными (например, A и B).

Логические основы ЭВМ

Яруллина Гульсиня Ситдиковна, преподаватель информатики

Статья отнесена к разделу: Преподавание информатики

Цели урока:

• развитие логического и алгоритмического мышления, памяти, внимательности
• дать студентам представление о том, как в компьютере при помощи логических элементов выполняются арифметические и логические операции.
• развитие познавательного интереса

Задачи преподавателя:

• на аналогиях из повседневной жизни показать, что логика хорошо реализуется при помощи электронных схем;
• познакомить студентов с логическими элементами;
• дать представление студентам о последовательности создания логического устройства.

Тип урока: урок объяснения нового материала

Методы: словесный, наглядно-иллюстративный, практический.

Организационные формы работы: фронтальная, групповая и индивидуальная

Оборудование: ПК, мультимедийный проектор,

Материалы к уроку:

• интерактивные ролики из Интернета в режиме on-line (http://somit.ru),
• презентация «Логические основы ЭВМ»

Ход урока

I. Организационный момент

Приветствие студентов, проверка отсутствующих, готовность к уроку, настрой их на дальнейшую работу.

II. Сообщение темы и целей урока.

Слайд 1.

Итак, тема нашего урока Логические основы компьютера. (Запись в тетради темы урока)

Слайд 2.

Ребята, сегодня на уроке мы с вами постараемся ответить на следующие вопросы:

• Какова роль математической логики в создании ЭВМ.
• Что такое логический элемент?
• Познакомимся с некоторыми логическими элементами компьютера;
• Познакомимся сборкой электрических цепей

Слайд 3.

III. Повторение пройденного материала. Фронтальный опрос.

Слайд 4.

• Как человек мыслит? (выделяет существенные признаки предмета, позволяющие отличить их от других, высказывает свою мысль, доказывает, делает вывод)

Вывод: т.е мышление всегда осуществляется через понятия, высказывания и умозаключения.

• Что в нашей речи является высказыванием, а что – нет? (Высказыванием является повествовательное предложение, в котором что-либо утверждается или отрицается).
• Как называется наука, которая занимается изучением форм и способов мышления? (Логика)

Слайд 5

• Чей этот портрет? (Аристотель) Кто кратко расскажет о нем?
• Как называется наука об операциях над высказываниями? (Алгебра логики)
• Как называется в алгебре логики простое высказывание? (Логическая переменная).
• Как ее обозначают в алгебре логики? (с помощью латинской буквы)
• Как называется составное высказывание (Логическая функция)
• Какие логические операции можно выполнить над высказываниями? (л.у, л.с, отрицание, импликацию, эквивалентность)

Если составное высказывание (л. функцию) выразить в виде формулы, то получится логическое выражение.

Слайд 6

• Запишите в виде логического выражения ответ на следующий вопрос: когда из крана польется вода? (Когда открыт кран А и открыт кран Б)

Слайд 7

когда из крана польется вода? (Когда открыт кран А или открыт кран Б)

• Как называется логическая операция, когда 2 простых высказывания соединяются с помощью союза и? или?

Слайд 8

ЗАПОМНИ

Слайд 9

• Как называется операция, которая образуется из высказывания с помощью добавления частицы «не» к сказуемому или использования оборота речи «неверно, что…». Логическое отрицание (инверсия)

Слайд 10

Вывод: назовите базовые логические операции

Операция конъюнкции на функциональных схемах обозначается знаком & (читается как «амперсэнд»), являющимся сокращенной записью английского слова and.

И если л. выражение содержит большое число операций, то сложно найти результат. Для приведения формулы к нормальной форме используют законы логики.

Слайд 11

• Какие законы логики знаете? (записать на доске)

IV. Изучение нового материала

Слайд 12

Тема урока

Слайд 13.

Роль математической логики в создании ЭВМ

Над возможностями применения логики в технике ученые и инженеры задумывались уже давно.

Посмотрим на микросхему. На первый взгляд ничего того, что нас удивило бы, мы не видим. Но если рассматривать ее при сильном увеличении она поразит нас своей стройной архитектурой. Чтобы понять, как она работает, вспомним, что она работает на электричестве, т.е. любая информация представлена в компьютере в виде электрических импульсов

Вариант диалога

Вопрос: Есть электрическое устройство, которым мы пользуемся каждый день. Оно реализует логическую операцию отрицания. Подумайте, что это за устройство?

Ответ: Выключатель. Если свет не горел, он его включает, если горел – выключает.

Интерактивный ролик 1 (http://somit.ru/informatika1.htm)

Итак, перед вами электрическая цепь, состоящая из источника тока, электрической лампочки, выключателя, вольтметра (понадобится для того, чтобы установить величину напряжения, соответствующего сигналу ВКЛЮЧЕНО в компьютерах) и конечно же соединительных проводников.

На кадре интерактивного ролика предоставляется возможность, щелкая по выключателю, переводить его в режим "ВКЛЮЧЕНО" или "ВЫКЛЮЧЕНО", одновременно сравнивая сигналы на клемме Х и ВЫХОДЕ, т.е. на лампочке.

Интерактивный ролик 2 (инверсия) (http://somit.ru/informatika2.htm)

Щелкая по выключателю, проверяем работоспособность электрической схемы и пробуем объяснить для себя и запомнить принцип работы данной электрической схемы

Интерактивный ролик 3 (конъюнкция) (http://somit.ru/informatika3.htm)

Щелкая по выключателю, проверяем работоспособность электрической схемы и пробуем объяснить для себя и запомнить принцип работы данной электрической схемы

Интерактивный ролик 4 (дизъюнкция) (http://somit.ru/informatika4.htm)

Щелкая по выключателю, проверяем работу

способность электрической схемы и пробуем объяснить для себя и запомнить принцип работы данной электрической схемы

Вывод: вы сейчас убедились, как хорошо реализуются логические операции в простейших схемах.

Недостатками контактных схем являлись их низкая надежность и быстродействие, большие размеры и потребление энергии. Поэтому попытка использовать такие схемы в ЭВМ не оправдала себя. Появление вакуумных и полупроводниковых приборов позволило создавать логические элементы с быстродействием от 1 миллиона переключателей в секунду. Именно такие электронные схемы нашли свое применение в качестве элементной базы ЭВМ.

Слайд 14

Что такое логический элемент компьютера?

Вся теория, изложенная для контактных схемах, была перенесена на электронные схемы. Элементы, реализующие базовые логические операции, назвали базовыми логическими элементами или вентилями. Как при строительстве дома применяют различного рода типовые блоки – кирпичи, рамы, двери и т.п., так и при разработке компьютера используют типовые электронные схемы. Каждая схема состоит из определенного набора типовых электронных элементов.

Логический элемент компьютера – это часть электронной логической схемы, которая реализует элементарную логическую функцию.

Тысячи микроскопических электронных переключателей в кристалле интегральной схемы сгруппированы в системы, выполняющие логические операции, т.е. операции с предсказуемыми результатами, и арифметические операции над двоичными числами. Соединенные в различные комбинации, логические элементы дают возможность компьютеру решать задачи, используя язык двоичных кодов.

V. Построение логических схем

Правило

1.     Определить число л. переменных

2.     Определить количество базовых логических операций и их порядок

3.     Изобразить для каждой логической операции соответствующий ей вентиль

4.     Соединить вентили в порядке выполнения логических операций

Пример.

Составить логическую схему для следующего логического выражения:

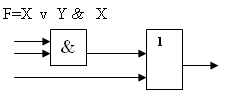
Ответ: 1v 0 & 1 = 1

Слайд 16

Задание 1

Слайд 17

Домашнее задание

Письменно:

Запишите данное высказывание в виде формулы

1.     Для сдачи экзамена необходимы знание или везение.

2.     Только умение и настойчивость приводят к достижению цели

Скачано с www.znanio.ru