Алгебра_8класс_Повторение_Неравенства_Методические рекомендации к уроку №5

Методические рекомендации к проведению урока

Тема урока: Повторение раздела «Неравенства»

Тип урока: урок-повторение

Цели обучения:

8.2.2.8

решать квадратные неравенства;

8.2.2.9

решать рациональные неравенства;

8.2.2.10

решать системы из двух неравенств, одно из которых линейное, а второе – квадратное;

8.2.2.11

решать системы и совокупности двух квадратных неравенств.

Цели урока:

·         решать квадратные неравенства: методом интервалов, графическим методом;

·         решать рациональные неравенства;

·         решать системы из двух неравенств, одно из которых линейное, а второе – квадратное;

·         решать системы двух квадратных неравенств;

·         решать совокупности двух квадратных неравенств.

Структура урока

1.    Организационный момент. Целеполагание.

2.    Повторение.

3.    Самостоятельная работа.

4.    Тест за раздел «Неравенства».

5.    Подведение итогов урока. Рефлексия.

Теоретический материал к уроку, определения к понятиям и др.

Определение. Неравенство, левая часть которого есть многочлен второй степени, а правая - нуль, называется квадратным неравенством.

Алгоритм решения квадратных неравенств, основанный на свойствах квадратичной функции.

–   Определить знак коэффициента а квадратичной функции и указать направление ветвей параболы.

–    Определить знак дискриминанта  квадратного трехчлена.

Если , то вычислить корни и отметить их на числовой прямой.

Если , то сразу перейти к следующему шагу.

–     Схематично изобразить параболу или представить ее положение на координатной плоскости.

–     По схематическому изображению параболы записать множество решений неравенства.

Метод интервалов.

Рассмотрим неравенства вида f (x) > 0 и f (x) < 0

•      Решить уравнение f (x) = 0;

•      Отметить все полученные корни на координатной прямой.

•      Выяснить знак (плюс или минус) функции f (x) на самом правом интервале. Для этого достаточно подставить в f (x) любое число, которое будет правее всех отмеченных корней;

•      Отметить знаки на остальных интервалах. Для этого достаточно запомнить, что при переходе через каждый корень знак меняется, за исключением сложных точек.

•      Выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имеет вид f (x) > 0, или знаком «−», если неравенство имеет вид  f (x) < 0.

Решение системы/совокупности неравенств с одной переменной.

1) решить каждое неравенство независимо одно от другого.

2) в ответ записать общие/все решения данных неравенств.

Инструкции к демонстрациям и технике безопасности.

Демонстрация материала осуществляется с помощью презентации PowerPoint. Слайды презентации содержат анимации, которые позволяют поэтапно вывести на экран решения и ответы к предложенным заданиям. Поэтому при показе презентации следует делать паузы после демонстрации заданий и постановки вопросов, давая учащимся время на их выполнение и обдумывание ответов.

Дополнительные методические рекомендации по организации урока.

Структура и организация урока нацелены на продуктивную деятельность учащихся при изучении новой темы, не допуская пассивного восприятия материала. В связи с этим учителю необходимо задавать учащимся вопросы высокого порядка, наталкивая их на «открытие» и освоение нового материала, при этом выдерживая паузы, необходимые для обдумывания.    

Дополнительные разноуровневые (на дифференциацию) задания.

Базовый уровень

А1. Какие из чисел  -3; 0; 2  являются решениями неравенства   ?

А2. Решите неравенство:

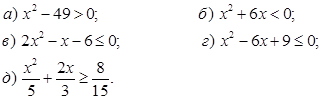
В1. При каких значениях  х  имеет смысл выражение  ?

Продвинутый уровень

Решите неравенства:

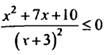
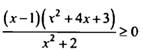
Рекомендации по формативному оцениванию.

Формативное оценивание производится на каждом этапе урока (самооценивание, взаимооценивание, оценивание учителем по критериям). Оценка путем наблюдения за вовлечением учеников в работу при выполнении заданий и за участием в диалогах. Прогресс, ответную реакцию на задания в парах, в группах необходимо отслеживать для того, чтобы оценить вклад каждого ученика и выявить наличие ошибок для их дальнейшей коррекции.

Ответы, критерии к заданиям, дополнительные материалы к уроку.

Ответы ко всем заданиям представлены в презентации и будут полезны для организации самооценивания или взаимооценивания учащихся.

Критерии оценивания к каждому блоку заданий прописаны в приложениях к уроку, а также указаны в краткосрочном плане.

Список полезных ссылок и литературы.

Алгебра. 8-класс: Учебник для 8 класса общеобразовательной школы с русским языком обучения/ А.Н. Шыныбеков – 3-издание. – Алматы: «Атамұра», 2012. 288 с.

Алгебра. 8-класс: Учебник для 8 класса общеобразовательной школы с русским языком обучения/ А.Е. Абылкасымова – Алматы: «Мектеп», 2008. 144 с.

Алгебра. 8  класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 21-е изд., испр. — М. : Мнемозина,

2014.