Конспект  бинарного урока  по информатике и математике

(Вычисление площади криволинейной трапеции методами приближенного вычисления в среде MS Excel и методом определенного интеграла.)

 

Данный урок целесообразно провести в дополнение к основным урокам при изучении электронной таблицы MS Excel.

Цель данного урока  дублирование и  повторение пройденной темы по алгебре, углубление понятий, связанных с интегральным исчислением. Используя возможности ЭТ (в частности применение и  копирование данных и  формул), мы рассмотрим три метода приближенного вычисления площади криволинейной трапеции и метод определенного интеграла и сделаем вывод о том, какой же способ дает наиболее точное значение.

 

 

ТЕМА  УРОКА:

Вычисление площади криволинейной трапеции методами приближенного вычисления в среде MS Excel и методом определенного интеграла.

 

Задачи урока:

 

Образовательные:

 1. Закрепление навыков вычисления  площади криволинейной трапеции с помощью  определенного интеграла и приближенных методов вычислений

2.Совершенствовать навыки работы в среде MS Excel.

3.Углублять и систематизировать знания работы с Мастером диаграмм.

 

Развивающие:

1. Способствовать развитию мышления, умения применять полученные знания при решении задач различной направленности.
2. Способствовать развитию представлений учащихся о прикладном значении программ MS-Office.

Воспитательные:

1. Воспитывать ответственность, коллективизм, взаимопомощь.
2. Воспитывать познавательный интерес к предмету.

 

Тип урока:

Урок совершенствование знаний, умений и навыков на основе полученных знаний в курсе дисциплин «Математики и Информатики»

 

Материально техническое оснащение:

1. Компьютеры с операционной системой Windows XP.
2. Программное обеспечение Microsoft Office, Excel XP.
3. Мультимедийный проектор. Экран.
4. Листы с индивидуальными заданиями – 14 шт

 

Ход урока

Организационный момент.

            Тема сегодняшнего урока: «Вычисление площади криволинейной трапеции методами приближенного вычисления в среде MS Excel и методом определенного интеграла.»

 

Мы с Вами прошли раздел интегрального исчисления, научились вычислять неопределенные и определенные интегралы, с помощью определенного интеграла научились решать физические и геометрические задачи.

Давайте вспомним.

 Вопросы:

1.     Что такое интегрирование?

 

         Ответ:  Интегрирование – нахождение функции по ее производной или по ее  дифференциалу

 

2.     Какие бывают интегралы?

           Ответ: Неопределенные и определенные

 

3.Чем отличается неопределенный интеграл от определенного?

 

           Ответ: у определенного интеграла есть пределы интегрирования, а у неопределенного их нет.

 

 

4.В чем состоит геометрический смысл определенного интеграла?

 

           Ответ: определенный интеграл от неотрицательной непрерывной функции есть площадь соответствующей криволинейной трапеции.

 

Вспомним немного истории: интегральное исчисление было предложено в 17 в. И.Ньютоном и Г. Лейбницем.

 

К сегодняшнему уроку Вам было задано подготовить небольшой доклад об истории возникновения интегрального исчисления.

 

Выступления студентов.

 

 

Сам знак  ∫ возник из первой буквы S латинского слова Summa. Но ведь при Евдоксе и Архимеде (400 г до н.э.) не было интегралов. Как же находили площади нестандартных фигур?

 

Возможные ответы учащихся …

 

1.     Методом прямоугольников (с недостатком и с избытком)

2.     Методом трапеций

 

  

Вопрос классу: Давайте вспомним: Что называют криволинейной трапецией?

         Криволинейной трапецией называется фигура, ограниченная отрезком  [a; b], графиком непрерывной функции не изменяющей своего знака на заданном отрезке и прямыми х=а и x=b.

(на доске через проектор)

 

          У                                         У                                  У                               У

                   у=f(x)                                                                      у=f(x)       

                                                                                                                        a                           b   Х

 

                                                                  y=f(x)

                                                                                                                                               

                                                                                      a    0                  b   Х                 y=f(x)

            0    a                b  Х           a  0                   b   Х       

 

Вычислим площадь криволинейной трапеции приближенными способами.

У каждого на столе лежат карточки с  двумя заданиями.

 

 

 

 

 

 

1.      Метод прямоугольников

 

                с недостатком                                                      с избытком

 

                    Y                                                                        Y

                  f(x_n)       y=f(x)                                              f(x_n)            y=f(x)

 

                   f(x₀)                                                               f(x₀)     

                                  S1                                                                     S1

 

                                  dx                                                                    dx

 

                        0     х₀                х_n         X                               0     х₀                х_n                X

 

            dx – шаг разбиения

            х₀ + dx = х₁                f(x₀) – значение функции в точке х₀

            …

            x_n-1 + dx = x_n               f(x_n) - значение функции в точке x_n

 

            S1пр = F(x₀) * dx                                                    _{n-1                                                n}

            S2пр = F(x₁) * dx                               S фигуры = Σ Si      S фигуры = Σ Si     

            …                                                        (_{с недостатком) i=0                 (c избытком)      i=1}       

Si пр = F(x_n-1) * dx

 

 

 

2.      Метод трапеций                                                     Х           y=f(x)

                                                                                    f(x_n)

     S1трап = (F(x₀) + F(x₁)) / 2 * dx

     S2трап = (F(x₁) + F(x₂)) / 2 * dx         

      …                                                                           f(x₀)

     Si трап = (F(x_n-1) + F(x_n)) / 2 * dx                                                        S

                                                                                                 dx

                                                                                 

                                    _n                                                     0     x₀             x_n         Y

              S фигуры = Σ Si     

                  _{трапеции        i=1}

 

На предыдущих уроках мы изучили функции ЭТ, составляли таблицы, строили диаграммы. Сегодня на уроке, используя возможности ЭТ, мы рассмотрим три метода приближенного вычисления площади криволинейной трапеции:

·        метод прямоугольников с недостатком;

·        метод прямоугольников с избытком;

·        метод трапеций.

Наша цель дублирование и повторение пройденной темы по алгебре, и углубление понятий, связанных с интегральным исчислением.

 

 

Реализуем все методы через электронную таблицу.

Что нам необходимо знать?

1.     Функцию

2.     Пределы интегрирования

3.     Шаг интегрирования (разбиения)

 

Рассмотрим на примере:        1. Функция Y=  ,

ограниченная прямыми y = 0, x = 1, x = 2

2. Пределы интегрирования [1,2]

3. Шаг интегрирования dx = 0.1

 

 

 

Ресурсы ЭТ

1.     Заголовочная часть.

2.     Начальное и конечное значения аргумента (пределы интегрирования).

3.     Шаг разбиения.

 

Заполним ЭТ в соответствии с тремя рассмотренными способами, при этом учтем следующее:

1.     Вспомним, что обозначает «######»  при работе с формулами или с числами? (Не хватает места для записи чисел или формул, следовательно необходимо увеличить ширину колонки)

2.     Можно ли заносить в одну ячейку числовую и текстовую информацию? (Нельзя)

3.     Какую команду следует использовать для облегчения многократного ввода и идентичного вычисления данных? (Копирование)

 

                                         

 

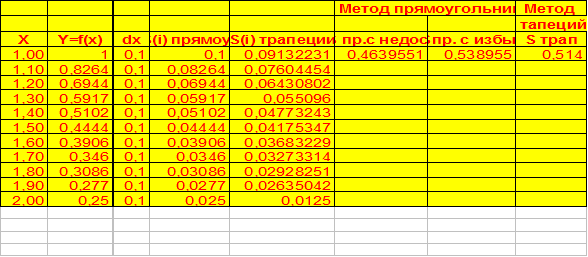
1.      Поменяем шаг интегрирования с dx = 0,1 на dx = 0,5 следовательно изменится количество значений аргумента и соответствующих им значений функций, поэтому применяя команду копирования необходимо взять заведомо большее количество значений аргумента.

2.      Рассмотрим графическое представление данной функции при различных dx.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Задание:

1.      Найти площадь криволинейной трапеции, заданной функцией Y=  всеми тремя способами. Сначала с шагом интегрирования dx = 0,1, а затем с шагом dx = 0,5.

2.      Сравнить результаты вычислений, полученных при вычислении через электронную таблицу с найденным значением интеграла данной функции

 

       = 0,5 кв. ед

 

Сравнив все полученные результаты, какой вывод можно сделать?

1.      От чего зависит точность вычисления площади криволинейной трапеции?

2.      Какой из способов дает более точное значение? Как вы думаете, почему?

 

Итак, подведем итог:

    Точность вычисления площади криволинейной трапеции зависит:

1.      От шага разбиения, т.е. шага интегрирования ( чем меньше шаг, тем больше точность вычисления.

2.      От метода, применяемого к функции.

3.      Наиболее точное значение вычисления площади криволинейной трапеции дает метод трапеций по отношению к точному результату 

4.      Самый точный результат получается при вычислении площади криволинейной трапеции с помощью определенного интеграла.

 

.

Домашнее задание: ( выдается на отдельных листочках каждому учащемуся)

 

 Используя методы приближенного вычисления площади криволинейной трапеции, найти площади фигур с помощью MS Excel и сравнить их с точным значением интеграла. Полученные значения записать в тетрадь и сделать вывод.

Найти площадь криволинейной трапеции   тремя различными способами и сравнить их с точным значением интеграла.    

 

Криволинейная  трапеция ограничена графиком функции У = 1/(Х + 2)²  +1 и прямыми   У = 0, Х = 0, Х = 2

 

Криволинейная  трапеция ограничена графиком функции У =  Х³ + 1 и прямыми У =  0,     Х = 0, Х = 2

 

     

  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Литература

 

 

1.     Н. Угринович Информатика и информационные технологии 10-11, Москва, Бином, Лаборатория знаний, 2007 г.

2.     Н. Угринович Практикум по информатике и информационным технологиям 10-11, Москва, Лаборатория базовых знаний, АО «Московские учебники», 2007 г.

3.     «Математический энциклопедический словарь», М., «Советская энциклопедия», 1988 г.

4.     В.С. Крамор «Повторяем и систематизируем школьный курс Алгебры и начала анализа», М., 1990 г.

5.     А.М. Рубиков, К.Ш. Шапиев «Элементы математического анализа», М., Просвещение, 1982 г.

6.     А.Н. Колмогоров и др. «Алгебра и начала анализа» учебник для 10 – 11 класса общеобразовательных учреждений, М., Просвещение, 2006 г.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

КАРТОЧКА 1

 

^1.       Задана функция  у= 1/х²

а) построить график заданной функции;

б) вычислить площадь криволинейной трапеции, ограниченной графиком этой функции и прямыми х=1, х=2 методом прямоугольников с недостатком с шагом разбиения dх=0,1

2.   Вычислить площадь криволинейной трапеции, ограниченной графиком заданной функции, прямыми х=1, х=2 с помощью определенного интеграла

 

 

 

 

КАРТОЧКА 2

 

1.  Задана функция  у= 1/х²

а) построить график заданной функции;

б) вычислить площадь криволинейной трапеции, ограниченной графиком этой функции и прямыми х=1, х=2 методом прямоугольников с избытком с шагом разбиения dх=0,1

2.  Вычислить площадь криволинейной трапеции, ограниченной графиком заданной функции, прямыми х=1, х=2 с помощью определенного интеграла

 

 

 

 

 

 

КАРТОЧКА 3

 

1.  Задана функция  у= 1/х²

а) построить график заданной функции;

б) вычислить площадь криволинейной трапеции, ограниченной графиком этой функции и прямыми х=1, х=2 методом прямоугольников с недостатком с шагом разбиения dх=0,5

2.  Вычислить площадь криволинейной трапеции, ограниченной графиком заданной функции, прямыми х=1, х=2 с помощью определенного интеграла

 

 

 

 

КАРТОЧКА 4

 

1. Задана функция  у= 1/х²

а) построить график заданной функции;

б) вычислить площадь криволинейной трапеции, ограниченной графиком этой функции и прямыми х=1, х=2 методом прямоугольников с избытком с шагом разбиения dх=0,5

2. Вычислить площадь криволинейной трапеции, ограниченной графиком заданной функции, прямыми х=1, х=2 с помощью определенного интеграла

 

 

 

 

 

 

КАРТОЧКА 5

 

1. Задана функция  у= 1/х²

а) построить график заданной функции;

б) вычислить площадь криволинейной трапеции, ограниченной графиком этой функции и прямыми х=1, х=2 методом трапеций с шагом разбиения dх=0,5

2.Вычислить площадь криволинейной трапеции, ограниченной графиком заданной функции, прямыми х=1, х=2 с помощью определенного интеграла

 

 

 

 

 

 

КАРТОЧКА 6

 

1. Задана функция  у= 1/х²

а) построить график заданной функции;

б) вычислить площадь криволинейной трапеции, ограниченной графиком этой функции и прямыми х=1, х=2 методом трапеций с шагом разбиения dх=0,1

2.Вычислить площадь криволинейной трапеции, ограниченной графиком заданной функции, прямыми х=1, х=2 с помощью определенного интеграла

 

 

 

 

 

КАРТОЧКА 7

 

1. Задана функция  у= 1/х²

а) построить график заданной функции;

б) вычислить площадь криволинейной трапеции, ограниченной графиком этой функции и прямыми х=1, х=2 методом трапеций с шагом разбиения dх=0,5

2.Вычислить площадь криволинейной трапеции, ограниченной графиком заданной функции, прямыми х=1, х=2 с помощью определенного интеграла

 

 

 

 

 

 

 

КАРТОЧКА 8

 

1. Задана функция  у= 1/х²

а) построить график заданной функции;

б) вычислить площадь криволинейной трапеции, ограниченной графиком этой функции и прямыми х=1, х=2 методом трапеций с шагом разбиения dх=0,1

2.Вычислить площадь криволинейной трапеции, ограниченной графиком заданной функции, прямыми х=1, х=2 с помощью определенного интеграла

 

 

 

КАРТОЧКА 9

 

1. Задана функция  у= 1/х²

а) построить график заданной функции;

б) вычислить площадь криволинейной трапеции, ограниченной графиком этой функции и прямыми х=1, х=2 методом прямоугольников с недостатком с шагом разбиения dх=0,1

2.Вычислить площадь криволинейной трапеции, ограниченной графиком заданной функции, прямыми х=1, х=2 с помощью определенного интеграла

 

 

 

 

КАРТОЧКА 10

 

1. Задана функция  у= 1/х²

а) построить график заданной функции;

б) вычислить площадь криволинейной трапеции, ограниченной графиком этой функции и прямыми х=1, х=2 методом прямоугольников с избытком с шагом разбиения dх=0,1

2. Вычислить площадь криволинейной трапеции, ограниченной графиком заданной функции, прямыми х=1, х=2 с помощью определенного интеграла

 

 

 

 

 

КАРТОЧКА 11

 

1. Задана функция  у= 1/х²

а) построить график заданной функции;

б) вычислить площадь криволинейной трапеции, ограниченной графиком этой функции и прямыми х=1, х=2 методом прямоугольников с недостатком с шагом разбиения dх=0,5

2. Вычислить площадь криволинейной трапеции, ограниченной графиком заданной функции, прямыми х=1, х=2 с помощью определенного интеграла

 

 

 

 

КАРТОЧКА 12

 

1. Задана функция  у= 1/х²

а) построить график заданной функции;

б) вычислить площадь криволинейной трапеции, ограниченной графиком этой функции и прямыми х=1, х=2 методом прямоугольников с избытком с шагом разбиения dх=0,5

2.Вычислить площадь криволинейной трапеции, ограниченной графиком заданной функции, прямыми х=1, х=2 с помощью определенного интеграла

 

 

 

 

 

 

КАРТОЧКА 13

 

1. Задана функция  у= 1/х²

а) построить график заданной функции;

б) вычислить площадь криволинейной трапеции, ограниченной графиком этой функции и прямыми х=1, х=2 методом трапеций с шагом разбиения dх=0,5

2.Вычислить площадь криволинейной трапеции, ограниченной графиком заданной функции, прямыми х=1, х=2 с помощью определенного интеграла

 

 

 

 

КАРТОЧКА 14

 

1. Задана функция  у= 1/х²

а) построить график заданной функции;

б) вычислить площадь криволинейной трапеции, ограниченной графиком этой функции и прямыми х=1, х=2 методом трапеций с шагом разбиения dх=0,1

2. Вычислить площадь криволинейной трапеции, ограниченной графиком заданной функции, прямыми х=1, х=2 с помощью определенного интеграла

 

 

 

 

 

Домашнее задание

 

 Используя методы приближенного вычисления площади криволинейной трапеции, найти площади фигур с помощью MS Excel и сравнить их с точным значением интеграла. Полученные значения записать в тетрадь и сделать вывод.

Найти площадь криволинейной трапеции   тремя различными способами и сравнить их с точным значением интеграла.    

 

Криволинейная  трапеция ограничена графиком функции

У = 1/(Х + 2)²  +1 и прямыми   У = 0, Х = 0, Х = 2

 

Криволинейная  трапеция ограничена графиком функции

У =  Х³ + 1 и прямыми У =  0,     Х = 0, Х = 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ФГОУ  РХТКИ

 

 

 

 

 

 

 

 

 

Методическая  разработка

бинарного урока

 

 

 

 Дисциплина  «Информатика и математика»

 

Тема урока « Вычисление площади криволинейной трапеции методами приближенного вычисления в среде MS Excel и методом определенного интеграла.»

 

Дата проведения    14 ноября 2011 г.

 

Преподаватели  Никулина И.В., Рыбалкина М. В.

 

 

 

 

 

 

 

 

 

 

 

План открытого  урока

 

Дисциплина       Информатика и математика

     Тема  Вычисление площади криволинейной трапеции методами приближенного вычисления в среде MS Excel и методом определенного интеграла.

 

Группа, дата    2М, 14 ноября

Вид занятия: комбинированный

Цель урока: повторение пройденной темы по математике, углубление понятий, связанных с интегральным исчислением и применение электронных таблиц при вычислении площади криволинейной трапеции.

 

Задачи урока:

-       дидактическая      закрепить навыки вычислений площади криволинейной трапеции, совершенствовать навыки работы в среде МS Excel

-       воспитательная    формировать познавательный интерес к предметам математики и информатики

-       развивающая      развитие мышления при решении задач различной напраленности

 

Обеспечение занятия:

1.      Листы с заданиями

2.      Компьютерное обеспечение

3.      Мультимедийный проектор, экран

Содержание занятия:

1.      Организационный момент урока — 3 мин.

2.      Активизация мыслительной деятельности студентов по математике — 20 мин.

1. Понятие интегрирования

2. Виды интегралов

3. Отличие интегралов

4. Геометрический смысл определенного интеграла

5. Выступление студентов с докладами об открытии интегрального исчисления

3.      Индивидуальная работа с карточками по математике — 22 мин

4.      Активизация мыслительной деятельности студентов по информатике — 15  мин

1. Применение обозначений при работе с формулами и числами.

2. Запись в ячейку числовой информации

3. Запись в ячейку текстовой информации

4. Использование команд для облегчения многократного ввода и идентичного вычисления данных

5.      Работа студентов по карточкам на компьютерах — 25 мин

6.      Подведение результатов урока — 3 мин

7.      Домашнее задание — 2 мин

 

 

  Преподаватели:  Рыбалкина М.В., Никулина И.В.

 

ПРОТОКОЛ № 1

от 14 ноября 2011 г.

    Обсуждение бинарного урока по дисциплинам «Информатика» и «Математика»

     Преподаватели: Никулина И.В., Рыбалкина М.В.

     Присутствовали: Макарова Н.Т., Сагина Н.В,, Синельщикова З.К., Назарова О.Г.

    Тема: Вычисление площади криволинейной трапеции методами приближенного вычисления в среде MS Excel и методом определенного интеграла.

 

    Цель проведения : повторение полученных знаний по математике и применение этих знаний на уроках информатике при использовании компьтерной техники

 

   Вид занятия : комбинированный бинарный урок

   Цель урока:  повторение пройденной темы по математике, углубление понятий, связанных с интегральным исчислением и применение электронных таблиц при вычислении площади криволинейной трапеции.

   Задачи урока указаны в плане.

   Обеспечение урока: Карточки с заданиями, мультимедийный проектор, экран, компьютеры.

   Ход занятия:

1.    Организационный момент.

2.    Преподаватель математики Рыбалкина М.В. активизировала мыслительную деятельность студентов, показывала слайды, студенты выступили с докладами, которые сопровождались презентацией на экране

3.    Затем в течение 20 минут студенты работали по индивидуальным заданиям, а студентка Лапина А. работала по своему заданию  у доски

4.    После того, как задания были выполнены, преподаватель информатики Никулина И.В.  аквизировала мыслительную деятельность студентов и они приступили к выполнению своих заданий на компьютерах

5.    Студентка Никитина А. выполнила свое задания на компьютере и продемонстрировала его на экране проекторе

6.    Оба преподавателя в конце урока сравнили полученные результаты, сделали выводы по методам вычислений, подвели итоги и выставили всем оценки

7.    Студенты получили домашнее задание.

  Урок был интересным. Кабинет информатики был подготовлен надлежащим образом. Преподаватели применили на уроке мультимедийный проектор,  подготовили и показали презентацию. Оба преподавателя четко, на высоком профессиональном уровне излагали весь материал. Студенты работали активно, подготовили интересные доклады, на вопросы преподавателей отвечали быстро и четко, показали хорошие знания по пройденной теме по математике и смогли их применить на уроке информатике, быстро и правильно выполнив задания на компьютерах.

Цели урока достигнуты, студенты хорошо  работали и по математике, и по информатике.

Замечаний по ведению урока нет. Пожелание: оформить методическую разработку по этому уроку.

 

 

 

 

 

 

Присутствовали:

 

Макарова Н.Т.

Сагина Н.В.

Синельщикова З.К.

Назарова О.Г.

 

 

      Председатель предметной комиссии                  Рыбалкина М.В.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ПРОТОКОЛ № 4

от 12 декабря 2012 г.

    Обсуждение открытого  урока по дисциплине   «Математика»

     Преподаватель:  Рыбалкина М.В.

     Присутствовали: Осипова Т.В., Сагина Н.В,, Синельщикова З.К., Назарова О.Г, Озерова О.В.

    Тема:  Корень n-й степени и его свойства

 

•   Цель проведения :  Создать условия для формирования у обучающихся целостного представления о корне n-ой степени, навыков сознательного и рационального использования свойств корня при решении различных задач.

 

   Вид занятия : комбинированный  урок

   Цель урока: познакомиться с понятием корня n- степени и научиться использовать свойства корня при решении задач.

   Задачи урока указаны в плане.

   Обеспечение урока:

    1. Опорный план на доске.

2.Презентация к уроку.

3.Раздаточный материал:

4.Карточки с заданием для индивидуальной работы.

 

   Ход занятия:

1.    Организационный момент.

2.    Преподаватель  Рыбалкина М.В. активизировала мыслительную деятельность студентов, показывала слайды, студенты выступили с докладами, которые сопровождались презентацией на экране.

3.    Затем в течение 15 минут студенты работали по индивидуальным заданиям, а студентка  Власенко Е. работала по своему заданию  у доски.

4.    Ребята работали с раздаточным материалом, затем проверили решения по слайдам.

5.    Преподаватель выставила оценки за работу на уроке

6.    Студенты получили домашнее задание.

 

  Урок был интересным. Преподаватель  Рыбалкина М.В.  применила на уроке мультимедийный проэктор,  подготовила и показала презентацию по данной теме. Студенты работали активно, подготовили интересные доклады, на вопросы преподавателя отвечали быстро и четко, показали хорошие знания  по математике и смогли их применить на уроке,  быстро и правильно выполнили индивидуальные  задания.

Цели урока достигнуты, студенты хорошо  работали.

Замечаний по ведению урока нет. Пожелание: оформить методическую разработку по этому уроку.

 

 

 

 

 

 

Присутствовали:

Осипова Т.В.

Сагина Н.В.

Озерова О.В.

 

 

 

 

 

 

 

 

 

      Председатель предметной комиссии                  Рыбалкина М.В.

 

 

 

 

 

 

ПРОТОКОЛ № 2

от 12 октября 2012 г.

    Обсуждение открытого  урока по дисциплине «Математика»

     Преподаватель: Рыбалкина М.В.

     Присутствовали: Осипова Т.В., Сагина Н.В, Михеева С.А.,

Некрылова Ю.Д.

    Тема: «Неопределенный интеграл и его свойства»

    Цель проведения: изучение данной темы

   Вид занятия: комбинированный  урок

   Цель урока: сформировать представление об интегральном исчислении, понять его сущность, развивать навыки при нахождении первообразных и неопределенного интеграла 

   Задачи урока указаны в плане.

   Обеспечение урока: портреты известных математиков, имеющих отношение к интегральному исчислению, презентация, карточки с заданиями, мультимедийный проектор, экран, компьютеры.

   Ход занятия:

1.Организационный момент.

2.Преподаватель математики Рыбалкина М.В. активизировала мыслительную деятельность студентов, показывала слайды,  которые сопровождались презентацией на экране, ребята записывали определения и свойства в тетрадь, рассматривали основные формулы интегрирования, активно работали и отвечали на вопросы преподавателя.

3.      Затем в течение 12 минут студенты работали по индивидуальным заданиям в подгруппах  в виде игры «Найди свою половинку», результатом которой появилось слово соответствующее теме данного урока.

4.      Ребята хорошо справились с заданием, ошибки были незначительны у некоторых учеников.

5.      Преподаватель в конце урока  подвела итоги и выставила всем оценки.

6.      Студенты получили домашнее задание.

  Урок был интересным.  Преподаватель применила на уроке мультимедийный проектор,  подготовила и показала презентацию, на высоком профессиональном уровне излагала весь материал. Студенты работали активно, на вопросы преподавателей отвечали быстро и четко, отлично справились с заданием игры «Найди свою половинку», работая в подгруппах. Цели урока достигнуты. Замечаний по ведению урока нет.

Пожелание: оформить методическую разработку по этому уроку.

 

 

 

 

Присутствовали:

 

Осипова Т.В.

 

Сагина Н.В

 

Михеева С.А.

 

Некрылова Ю.Д.

 

 

      Председатель предметной цикловой  комиссии                              Осипова Т.В.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Скачано с www.znanio.ru