Дискретна та неперервна одногалузеві динамічні моделі

Дискретна та неперервна одногалузеві динамічні моделі

Нехай усі фактори залежать від часу, тоді можна записати

                                                                 (5.1)

          Припустимо, що валові інвестиції I у тому ж році, коли була вироблена валова продукція Х, цілком використовуються на приріст ОВФ і амортизаційні відрахування.

У дискретній формі можна представити у вигляді

                                                                                (5.2) 

           де – приріст капіталу в році t

           K_t – виробничий капітал у році t,

           q – коефіцієнт пропорційності (параметр моделі),

          – амортизаційні відрахування,

          μ – коефіцієнт амортизації.

Запишемо рівняння (5.2) у неперервній формі.

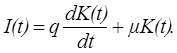
Звідси виведемо рівняння руху капіталу 

                              _,

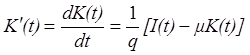Повернемося до дискретної форми. Використаємо вирази (5.1) та (5.2)

Якщо припустити, що проміжні витрати є пропорційними випускові валової продукції

де а-коефіцієнт виробничих витрат, то можна записати

                                                              (5.3)

З виразу (5.3) одержуємо вираз

,

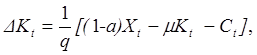який являє собою дискретну одногалузеву динамічну модель.

         У неперервній формі ця модель має вигляд

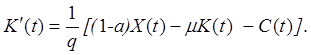                                                         (5.4)