Поделиться
Двоичная система счисления..doc
3урок, 8 класс
Учитель: Брух Т.В.
Дата:______________
Тема урока: «Двоичная система счисления».
Цели и задачи урока: освоить перевод десятичных чисел в двоичную
систему счисления и двоичных чисел в десятичную систему счисления. Уметь выполнять
операции сложения и умножения над двоичными числами. Понимать роли
фундаментальных знаний как основы современных информационных технологий
Планируемые образовательные результаты:
личностные – понимание роли фундаментальных знаний как основы современных информационных технологий; обосновывать свою позицию, высказывать своё мнение.
предметные – навыки перевода небольших десятичных чисел в двоичную систему счисления и двоичных чисел в десятичную систему счисления; умения выполнения операций сложения и умножения над небольшими двоичными числами;
метапредметные – умение анализировать любую позиционную систему счисления как знаковую систему.
Решаемые учебные задачи:
1) рассмотрение двоичной системы счисления как знаковой системы;
2) рассмотрение правила перевода двоичных чисел в десятичную систему счисления;
3) рассмотрение правила перевода целых десятичных чисел в двоичную систему счисления;
4) знакомство с операциями сложения и умножения в двоичной системе счисления.
Ход урока:
1. Организационный момент
2. Проверка домашнего задания
3. Изучение нового материала
Система счисления — это знаковая система, в которой приняты определённые правила записи чисел. Знаки, с помощью которых записываются числа, называются цифрами, а их совокупность — алфавитом системы счисления.
Двоичная система счисления издавна была предметом пристального внимания многих ученых.
Все позиционные системы счисления “одинаковы”, а именно, во всех них выполняются арифметические операции по одним и тем же правилам:
- справедливы одни и те же законы арифметики: коммутативный (переместительный), ассоциативный (сочетательный), дистрибутивный (распределительный);
- справедливы правила сложения, вычитания, умножения и деления столбиком;
- правила выполнения арифметических операций опираются на таблицы сложения и умножения.
Сейчас научимся, переводит из двоичной системы счисления в десятичную систему счисления и наоборот.
Примеры двоичной СС:
1) 1001112=
1*20+1*21+1*22+0*23+0*24+1*25=1+2+4+32 = 3910
2) 101101102 = (1·27)+(0·26)+(1·25)+(1·24)+(0·23)+(1·22)+(1·21)+(0·20) = 128+32+16+4+2 = 18210
Научимся переводить из десятичной системы счисления в двоичную систему счисления.
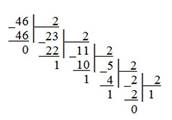Нужно последовательно делить данное число
на n до получения
числа, меньшего n. Затем записать остатки в обратном порядке. Это будет
искомое число.
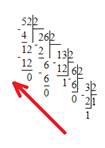Примеры десятичной СС:
1) 5210 =
Ответ: 1101002
2) 4610=
Ответ: 1011102
|
Арифметические операции в двоичной системе счисления I. Сложение. Рассмотрим сложение чисел в двоичной системе счисления. В его основе лежит таблица сложения одноразрядных двоичных чисел: |
|
0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10 |
Важно обратить внимание на то, что при сложении двух единиц происходит переполнение разряда и производится перенос в старший разряд. |
|
II. Вычитание. Рассмотрим вычитание двоичных чисел. В его основе лежит таблица вычитания одноразрядных двоичных чисел. При вычитании из меньшего числа (0) большего (1) производится заем из старшего разряда. В таблице заем обозначен 1 с чертой: |
|
|
0 – 0 = 0 0 – 1 = 1 1 – 0 = 1 1 – 1 = 0 |
Вычитание многоразрядных двоичных чисел происходит в соответствии с вышеприведенной таблицей вычитания с учетом возможных заемов из старших разрядов. |
III. Умножение.
0 * 0 = 0
0 * 1 = 0
1 * 0 = 0
1 * 1 = 1
4. Закрепление, выполнение заданий
Самостоятельная работа по теме:
«Перевод целых чисел из двоичной системы счисления в десятичную и обратно»
1 вариант
1) Переведите числа из десятичной системы в двоичную:
a) 371
b) 25
c) 18
d) 101
2) Переведите числа из двоичной системы в десятичную:
a) 10101
b) 1001
c) 1011
d) 111
3) Выполните сложение
4) а) 11001 +101 = 1 1110
5) б) 11001 +11001 = 110010
6) Выполните вычитания.
7) а) 11001-1001 = 10000 б) 1011-110 = 101
8) Выполните умножение:
9) а) 1101 * 1110 = 1011 0110 б) 1010 * 110 = 11 1100
Самостоятельная работа по теме:
«Перевод целых чисел из двоичной системы счисления в десятичную и обратно»
2 вариант
1) Переведите числа из десятичной системы в двоичную:
a) 189
b) 35
c) 16
d) 111
2) Переведите числа из двоичной системы в десятичную:
a) 1101
b) 10101
c) 10001
d) 10011
Выполните сложение
а) 11001 +101 = 1 1110
б) 11001 +11001 = 110010
Выполните вычитания.
а) 11001-1001 = 10000 б) 1011-110= 101
Выполните умножение:
а) 1101 * 1110 = 1011 0110 б) 1010 * 110 = 11 1100
5. Итог урока. Домашнее задание
|
100112 → А10 |
4610 → А2 |
|
1011012 → А10 |
67210 → А2 |
|
101112 → А10 |
93410 → А2 |
|
1001012 → А10 |
32510 → А2 |
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
