Экономическая задача в ЕГЭ по математике профильного уровня

Экзамен – это испытание не только знаний, но и хладнокровия, и способности действовать в сложной ситуации. На ЕГЭ по математике экономические задачи, пугают  многих выпускников. Действительно ли настолько страшны «банковские» задачи? Выпускникам необходимо преодолеть страх, выработать уверенность, чтобы ученик мог сказать себе: «Да, задача необычная, но я знаю общий подход к решению таких задач – справлюсь и на этот раз».

Самое необходимое для решения задачи экономического содержания в ЕГЭ по математике (профильный уровень)

•      1)  1% - это 0,01

•      2)  Основные соотношения и выражениями, встречающиеся при решении задач на проценты:

•      Число a составляет p% от числа в:   a =  0,01bp

•      Число а увеличили на p%:   a·(1+0,01p)

•      Число а увеличили сначала на p%, а потом еще на q%: a·(1+0,01p)·(1+0,01q)

•      Число а уменьшили на p%:   a·(1 - 0,01p)

Задачи, связанные с изменением величины

•      Пусть S_o – первоначальная величина, S – новая величина.

•      Повышение   на a%                 n раз на a%         

   S= S_o ·(1+0,01a)                    S= S_o ·(1+0,01a)ⁿ 

•         Понижение  на a%              n раз на a%         

    S= S_o ·(1-0,01a)                   S= S_o ·(1-0,01a)ⁿ 

Тематика задач экономического содержания в ЕГЭ по математике (профильный уровень)

•      Задачи на кредиты с аннуитетными (равными) платежами

•      Задачи на кредиты с дифференцированными платежами

•      Задачи на вклады и инвестиции

•      Задачи на оптимизацию, решаемые при помощи производной

Рассмотрим все варианты задач более подробно.

1 тип. Выплаты кредита производятся  равными платежами. Эта схема еще называется «аннуитет». К первому типу относятся также все задачи, где известны  платежи (или дана закономерность именно для платежей).

1. В июле 2022 года планируется взять кредит на некоторую сумму. Условия возврата таковы:

– в январе каждого года долг увеличивается на 20% по сравнению с предыдущим годом;

– с февраля по июнь нужно выплатить часть долга одним платежом.

Определите, какую сумму взяли в кредит, если известно, что кредит был выплачен четырьмя равными платежами (то есть за четыре года) и общая сумма выплат составила 311040 рублей.

Решение. Так как в задаче все четыре платежа равны между собой, то речь идет о аннуитетных платежах. Пусть ежегодный платеж по кредиту равен X млн рублей. Тогда каждый год долг увеличивается на 20%, то есть в n=1,2 раз, и уменьшается на X млн рублей. Обозначим начальную сумму S. Имеем:

S млн рублей – начальная сумма

n=0.01a = ставка по кредиту

x млн рублей – ежегодный аннуитетный платеж

Так как кредит был погашен за четыре года, то . Для облегчения вычисления можно заменить 1+n = Y.

Общая сумма выплат равна  Отсюда .

Ответ: 201300 рублей.

2. 31 декабря 2020 года Пётр взял в банке некоторую сумму в кредит под некоторый процент годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на a%), затем Пётр переводит очередной транш. Если он будет платить каждый год по 2 592 000 рублей, то выплатит долг за 4 года. Если по 4 392 000 рублей, то за 2 года. Под какой процент Пётр взял деньги в банке?

Используя решение предыдущей задачи, обозначим S млн рублей – начальная сумма

n=0.01a - ставка по кредиту

x млн рублей – ежегодный аннуитетный платеж

Получаем систему из двух условий

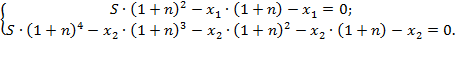
Выполняя подстановку S из первого уравнения во второе и преобразование многочлена, получаем

,

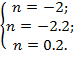
Два отрицательных корня не удовлетворяют условию задачи. n=0.2 или a=20%. Ответ: 20%.

2 тип.  Выплаты кредита подбираются так, что  сумма долга уменьшается равномерно. Это так называемая «схема с дифференцированными платежами». Ко второму типу относятся также задачи, где известна закономерность уменьшения суммы долга.

3. 15 декабря планируется взять кредит в банке на 21 месяц. Условия возврата таковы:

–                    1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;

–                    со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

–                    15-го числа каждого месяца с 1-го по 20-й долг должен быть на 30 тысяч рублей меньше долга на 15-е число предыдущего месяца;

–                    к 15-му числу 21-го месяца кредит должен быть полностью погашен.

Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1604 тысячи рублей?

По условию задачи m = 21, конечная сумма S _к = 1604 тыс., x=30 тыс., процентная ставка равна a = 3%. Пусть .

Значения платежей в этом случае находим по данным 2, 3, 5 столбцов таблицы.

,

,

…..

откуда находим S = 1100 тыс.

Ответ: 1100 тыс.

Напомним критерии оценивания

Спасибо за внимание! Желаем успехов!