
Елементарна теорія статичної моделі «витрати – випуск»
Для зручності математичного дослідження модель записують у векторно-матричній формі
![]()
де ![]() - одинична
матриця розміру
- одинична
матриця розміру ![]() ,
,
З погляду загальної теорії керування можна розглянути:
задачу аналізу або спостереження
![]()
задачу синтезу або планування
![]() ,
,
(показує процес планування валової продукції по заданому вектору кінцевої продукції).
Вектор валової продукції можна знайти за формулою
![]() =(I-A)-1
=(I-A)-1![]() ,
,
G=(I-A)-1,
![]() =G
=G![]() ,
,
де G - обернена матриця Леонтьєва або мультиплікатор Леонтьєва. Матриця G дорівнює
G=(Gij),
![]() ,
, ![]() .
.
Ця матриця зветься матрицею коефіцієнтів повних матеріальних витрат. Елемент Gij показує потребу в валовій продукції і-ої галузі для виробництва одиниці кінцевої продукції j-ї галузі.
Виникає питання відносно умов, за
яких існує така матриця (I-A)-1 , що для будь-якого
невід'ємного вектора ![]() ,
, ![]() ≥0, вектор (I-A)-1
≥0, вектор (I-A)-1![]() також невід'ємний. Матриця А
зветься невід'ємною, якщо всі її елементи є невід'ємними. Для економічних
систем матриця А завжди невід'ємна, але вона має бути також
продуктивною.
також невід'ємний. Матриця А
зветься невід'ємною, якщо всі її елементи є невід'ємними. Для економічних
систем матриця А завжди невід'ємна, але вона має бути також
продуктивною.
Умови продуктивності матриці А зв'язані з використанням одного з тверджень:
1) максимальне власне число λ(A) матриці А менше 1;
2) матриця (I-A) має невід'ємну обернену матрицю;
3) матричний ряд
I+A+A2+...+Ar+… = ![]() ,
,
A0=I,
(так званий ряд Неймана матриці А) збігається, при цьому його сума дорівнює оберненій матриці (I-A)-1
![]() =(I-A)-1,
=(I-A)-1,
4) послідовні головні мінори матриці (I-A) додатні.
З умови 3) випливає, що рішення задачі синтезу можна одержати итераційно, обчислюючи по формулі:
![]()
![]()
де приблизне рішення задачі ![]() одержане
по попередньому рішенню
одержане
по попередньому рішенню ![]() .
.
Виконаємо пошук власних чисел матриці ![]()
![]()
де - ![]() власний
вектор.
власний
вектор.
Приклад: дано матрицю ![]()
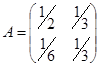 . Необхідно
знайти
. Необхідно
знайти ![]() і
і 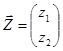 .
.
Величини ![]() і
і
![]() зв'язані рівнянням
зв'язані рівнянням
![]() .
.
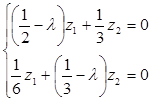
Щоб така система рівняння мала ненульове рішення, її визначник має дорівнювати 0.
![]() ;
;
![]() ;
;
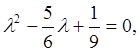
![]()
![]() ;
; ![]() ;
;
Виконаємо перевірку:
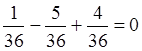 ,
,
![]() ,
,
таким чином для 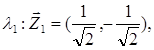
для 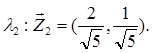 .
.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.