ЭТАПЫ МОДЕЛИРОВАНИЯ. ТЕОРИЯ ИГР. МОДЕЛИРОВАНИЕ ДВИЖЕНИЯ. ДИСКРЕТИЗАЦИЯ

7-8 урок, 11 КЛАСС – ТЕОРИЯ

Учитель: Брух Т.В.

Дата:______________

Тема урока: «Этапы моделирования. Теория игр. Моделирование движения. Дискретизация»

цель урока:

1.      Научиться анализировать множество вариантов развития ситуации.

2.      Освоить понятия: стратегия игры, выигрышная стратегия, дерево игры.

3.      Овладеть методом анализа дерева игры.

4.      Научится находить вариант хода, приводящий к выигрышу.

Ход урока:

1. Организационный момент

2. Проверка домашнего задания

3. Изучение нового материала

Слайд 2:

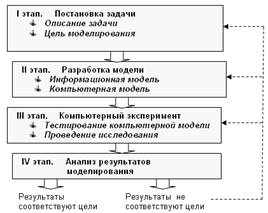Слайд 3:

Теория игр – это раздел прикладной математики, посвященный изучению математических методов поиска оптимальных стратегий в играх.

При этом под «играми» понимают любые процессы, в которых участвуют две или более сторон.

Игра с полной информацией — термин, обозначающий логическую игру, в которой для соперников отсутствует элемент неопределённости.

Игра рассматривается как определенный математический объект, который включает игроков, набор стратегий для каждого игрока и выигрыши игроков для каждой комбинации стратегий. Т.е. игру можно рассматривать как математическую модель.

Выражение «детерминированная игра» употребляют для такой игры, где при определённом её состоянии одно и то же действие будет всегда приводить к одному и тому же новому состоянию игры (отсутствует элемент случайности).

Слайд 4: Игра является игрой с полной информацией, если

n  игроки воздействуют на игровую ситуацию дискретными действиями — ходами, порядок ходов определён правилами и не зависит от таких параметров, как скорость реакции игроков (то есть очередной ход делает тот, кто должен его сделать по правилам, а не тот, кто первым догадался или успел его сделать);

n  в любой момент игры все игроки имеют полную информацию о состоянии игры, то есть о позиции и всех возможных ходах любого из игроков.

n  стратегия игрока в игре  — это полный план действий при всевозможных ситуациях, способных возникнуть. Стратегия определяет действие игрока в любой момент игры и для каждого возможного течения игры, способного привести к каждой ситуации.

n  набор стратегий — стратегии для каждого из игроков, которые полностью описывают все действия в игре. Набор стратегий обязан включать одну и только одну стратегию для каждого игрока.

Слайд 5:

Для любой детерминированной игры с полной информацией, теоретически, можно просчитать все возможные ходы игроков и определить последовательность ходов (алгоритм), которая гарантированно приведёт по крайней мере одного из них к выигрышу или ничьей.

Методы теории игр находят широкое применение в экономике, политологии, психологии, биологии и т.п. К играм с полной информацией относятся детерминированные настольные игры (например, шахматы, шашки, крестики-нолики и др.).

Для большинства из них алгоритм выигрыша или гарантированной ничьей неизвестен,  хотя теоретически он существует. На практике вариантов слишком много, чтобы их можно было построить и проанализировать за приемлемое время.

Слайд 6:

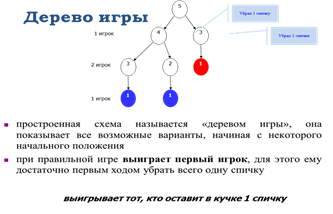
Выигрышные и проигрышные позиции

·                         все позиции в простых играх делятся на выигрышные и проигрышные

·                         выигрышная позиция – это такая позиция, в которой игрок, делающий первый ход, обязательно выиграет при любых действиях соперника, если не допустит ошибки; при этом говорят, что у данного игрока есть выигрышная стратегия – алгоритм выбора очередного хода, позволяющий ему выиграть

·                         если игрок, делающий первый ход, находится в проигрышной позиции, то он обязательно проиграет, если ошибку не сделает его оппонент; в этом случае говорят, что у данного игрока нет выигрышной стратегии; таким образом, общая стратегия игры состоит в том, чтобы своим ходом создать проигрышную позицию для оппонента

Слайд 7: Анализ выигрышных ходов

Анализ производится исходя из  того, что оба игрока располагают всей необходимой информацией об игру и стремятся к выигрышу. При решении нужно «по очереди играть за каждого игрока», каждый раз выбирая наиболее выгодный для этого игрока вариант хода.

Суть анализа (игрок 1 – это игрок, который делает первый ход начиная игру):

•      если в дереве игры имеется хотя бы один путь, который ведет от корня дерева к концевым вершинам с выигрышем игрока 1, и на этом пути нет никаких выигрышных ходов игрока 2, то при правильной стратегии поведения в данной игре всегда будет выигрывать игрок, делающий первый ход, а указанный путь отмечает выигрышный для него первый ход;

•      если в дереве игры для каждого хода игрока 1 встречается хотя бы один путь, ведущий к выигрышу игрока 2, то при правильной стратегии поведения в данной игре всегда будет выигрывать игрок 2, а указанный путь отмечает выигрышный для него первый ход, но для игрока 2 – это проигрышная стратегия.

Слайд 8:

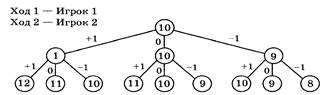
Для примера, рассмотрим задачу, когда n=10. Тогда Маша может сходить (2,8), (3,7), (4,6) и (5,5). Запишем это в виде графа. (Такой граф мы будем называть деревом игры). Продолжим рисовать граф. Его анализ покажет, что Маше не выгодно ходить первым ходом (2,8) или (4,6), что может привести к позиции (2,2,2,4), которая приведет ее к проигрышу. Поэтому если она хочет выиграть своим первым ходом она сходит (5,5) или (3,7), что гарантированно приведет ее к победе независимо от ходов Пети. Это и будет ее выигрышной стратегией.

Итак, выигрышная стратегия — это такое правило совершения ходов, при соблюдении которого игрок добьется выигрыша при любых ответных ходах противника.

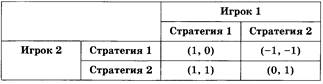
Слайд 9: В теории игр используют три основные формы записи:

·        в виде платёжной матрицы, которая имеет вид двумерной матрицы, размерность которой определяется количеством возможных стратегий каждого игрока;

·        в виде ориентированного дерева, которое имеет вид древовидного графа

·        в виде таблицы, очень удобна, если каждый ход может быть реализован большим числом разных вариантов

Слайд 10: Игра «Спички»

Правила:

n   сначала в кучке лежит 5 спичек;

n   два игрока убирают спички по очереди, причем за 1 ход можно убрать 1 или 2 спички;

n  выигрывает тот, кто оставит в кучке 1 спичку

Слайд 11:

4. Практическая работа

Слайд 12:

а) В кучке лежит 10 спичек. Игроки по очереди берут спички из кучки. За один ход разрешается взять 1 или 2. Проигрывает тот, кто делает последний ход.
б) То же самое, но в кучке 12 спичек.
в) То же самое, но в кучке 20 спичек, и можно брать от 1 до 4 спичек зараз.

Решение. а), б) Стратегия: сделайте так, чтобы противнику всегда доставалось число спичек, кратное трём, плюс 1, то есть 1, 4, 7, 10, ….
в) Стратегия: сделайте так, чтобы противнику всегда доставалось число спичек, кратное пяти, плюс 1, то есть 1, 6, 11, 16, ….

Слайд 13: Каким должен быть первый ход выигравшего игрока?

n  Каждый хочет выиграть!

n  Никто не ошибается!

n  Выигрыш зависит только от начального положения и правил игры.

5. Домашнее задание: стр 86, упр  14, 15, Параграф 9 - конспект

Скачано с www.znanio.ru