Формирование и развитие функциональной математической грамотности посредством современных педагогических технологий и практико-ориентированных заданий
Информационная карта инновационного педагогического опыта
/практики/
|
ФИО |
Мищенко Оксана Николаевна |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Образовательная организация |
МОУ «Школа-интернат среднего общего образования с. Ныда» |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Должность |
Учитель математики |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Стаж работы в должности |
25 лет |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
1. Тема инновационного педагогического опыта |
Формирование и развитие функциональной математической грамотности посредством современных педагогических технологий и практико-ориентированных заданий |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
2. Источник изменений |
Формирование готовности учащихся 5-9 классов для развития функциональной математической грамотности в рамках проведения международного исследования PISA. |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
3. Идея изменений |
Математическая формула, которая позволит сформировать у обучающихся в процессе изучения математики и других дисциплин качества мышления, необходимые для полноценного функционирования человека в современном обществе. «ОВЛАДЕНИЕ = УСВОЕНИЕ + ПРИМЕНЕНИЕ ЗНАНИЙ НА ПРАКТИКЕ» Как учитель математики, я прекрасно понимаю важность развития математической грамотности моих учеников, вижу в этом с одной стороны насущную необходимость в развитии способности обучающихся применять полученные в школе знания и умения в жизненных ситуациях Для этого в своей практике я использую такие технологии как КСО, ИОСО, компетентностно-ориентированные задания, практико-ориентированные задачи. |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
4. Концепция изменений: |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Актуальность |
В связи с тем, что школьники в международных исследованиях показывают низкий уровень математической грамотности перед учителями встала проблема в повышении данного показателя с помощью инновационных технологий обучения. |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Новизна |
1. Использование инновационных технологий в учебном процессе для формирования математической грамотности с целью повышения результативности обучения математике. 2. Вовлечение каждого обучающегося в процесс обучения. 3. Развитие творческих способностей. |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ожидания |
Повышение качества математической грамотности, снижение уровня тревожности, улучшение психологической активности обучающихся. |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Затруднения в реализации |
1. Основная масса учителей проводит традиционные уроки. 2. Слабое владение инновационными технологиями обучения. |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Риски |
1. Не формируется функциональная грамотность обучающихся. 2. Низкая мотивация у обучающихся. |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
5. Условия реализации изменений (предполагаемого опыта работы) |
В школе создана достаточная материальная база. Я - учитель высшей категории владею инновационными технологиями, использую разные методики для формирования функциональной математической грамотности на уроке и на внеурочных занятиях. |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
6. Результат изменений (использование предлагаемых способов обучения и воспитания) |
Проблема формирования функциональной грамотности требует изменений к содержанию деятельности на уроке. Научиться действовать ученик может только в процессе самого действия, а ежедневная работа учителя на уроке, образовательные технологии, которые он выбирает, формируют функциональную грамотность обучающихся. Обучающиеся должны уметь решать любые поставленные перед ними задачи. В зависимости от сложности задания выделены три уровня математической компетентности: Первый уровень включает воспроизведение математических фактов, методов и выполнение вычислений; Второй – установление связей и интеграцию материала из разных математических тем, необходимого для решения поставленной проблемы; Третий – математические размышления, требующие обобщения и интуиции. Практическая направленность инновационных технологий обучения повысить степень самостоятельности, инициативность обучающихся, приобретение обучающимися опыта исследовательски-творческой деятельности; это способствует развитию функциональной грамотности, повышению математической грамотности. Обучающиеся 9б класса (14 чел.) (работала в данном классе первый год), выполняя пробные ОГЭ по математике первую часть, справились с заданиями, проверяющими математическую грамотность:
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
7. Описание инновационного опыта (размещение как приложение в формате статьи) |
«Математическая грамотность – способность человека определять и понимать роль математики в мире, в котором он живет, высказывать хорошо обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину». Проблема: обучающиеся по итогам международных исследований «PISA» показывают низкий уровень «математической грамотности». Цель: с помощью различных образовательных технологий наряду с формированием предметных знаний и умений обеспечивать развитие у обучающихся математической грамотности. В дальнейшем это умение будет способствовать успешности выпускника школы во взрослой жизни. Задачи: · научить распознавать проблемы, возникающие в окружающей действительности, которые могут быть решены средствами математики; · научить формулировать эти проблемы на языке математики; · научить решать эти проблемы, используя математические знания и методы; · научить анализировать использованные методы решения; · научить интерпретировать полученные результаты с учетом поставленной проблемы; · научить формулировать и записывать окончательные результаты решения поставленной проблемы. Математическая грамотность включает в себя математические компетентности, которые нужно формировать через специально разработанную систему задач: 1 группа – задачи, в которых требуется воспроизвести факты и методы, выполнить вычисления; 2 группа – задачи, в которых требуется установить связи и интегрировать материал из разных областей математики; 3 группа – задачи, в которых требуется выделить в жизненных ситуациях проблему, решаемую средствами математики, построить модель решения». Формирование ключевых компетентностей посредством задач позволяет реализовать компетентностный подход на уроках математики как средство повышения математической грамотности учащихся. Ученики должны активно принимать участие на всех этапах учебного процесса: формулировать свои собственные гипотезы и вопросы, консультировать друг друга, ставить цели для себя, отслеживать полученные результаты. Прочное усвоение материала достигается посредством учебного процесса, в центре которого находится ученик, поэтому на протяжении всех уроков необходимо: • Создание той среды, которая позволяет личности чувствовать себя свободно и безопасно в процессе обучения. • Формирование саморегулирования, что обеспечивает самонаправленность, самостоятельное определение проблемы и цели, самостоятельный выбор стратегий для достижения целей. • Развитие критического мышления, что способствует осмыслению, оценки, анализу и синтезу информации, которые послужат основанием к действию. • Оценивание обучения, развития собственного понимания и определения обучения, для дальнейшего совершенствования. В связи с этим я использую в своей практике инновационные технологии: ИОСО, КСО, компетентностно-ориентированные задания и практико-ориентированные задачи. Основой ИОСО является индивидуально-ориентированный учебный план (ИОП). План предоставляет каждому обучающемуся, в зависимости от своих способностей, желаний, самочувствия, выбрать уровень выполнения заданий, темп усвоения учебного материала, тем самым создавая условия для движения по коллективному учебному маршруту сообразно своим индивидуальным способностям. Приложение 1. Включить учеников в активное усвоение и передачу информации и опыта удается при организации обучения в формах КСО. На первом этапе это лучше делать в парной организационной форме, причем начинать с пар постоянного состава. Пара может состоять как из примерно равных по силе учеников, так и учеников разноуровневых, где сильный помогает слабому. Однако учителю следует подобрать наиболее психологически совместимых учеников. Необходимо, чтобы обучающихся научились контролировать друг друга, задавать друг другу вопросы, работать с текстом , выполнять и задавать друг другу задания. Сначала для этого служат карточки «шпаргалки», в которых расписаны все действия учащихся. Применение методик КСО на уроках математики позволяет интенсифицировать процесс обучения, а также повышает квалификацию учителя. Учитель на этих уроках активно включается в процесс обучения, находится как бы внутри него, глубже познаёт учащихся, а значит более продуктивно работает. Приложение 2. Важнейшим видом учебной деятельности при обучении школьников математике является решение задач. Поэтому я формирую ключевые компетентности через специальные компетентностно-ориентированные задачи, аналогичные задачам для проверки математической грамотности. Компетентностными называются те задачи, которые удовлетворяют следующим требованиям: · Общекультурная и социальная значимость получаемого результата, это обеспечивает познавательную мотивацию учащегося; · Цель решения компетентностной задачи заключается не столько в получении ответа, сколько в присвоении нового знания (метода, способа решения, приема), с возможным переносом на другие предметы; · По структуре эти задачи нестандартные, т.е. в структуре задачи неопределены некоторые из ее компонентов; · Возможно наличие нескольких путей решения. Компетентностные задачи составлены так, что имеют проблемный характер и требуют применения знаний из разных разделов одной предметной области (математика) или из разных предметных областей, или же знаний из жизни. В связи с этим задачи можно разделить на предметные (математические), межпредметные и практические. Так как таких задач в учебниках, учебных пособиях, дидактических материалах немного, приходиться их составлять самостоятельно или искать в интернете. Решение задач практического содержания способно привить интерес ученика к изучению математики. Такие задания изменяют организацию традиционного урока. Они базируются на знаниях и умениях, и требуют умения применять накопленные знания в практической деятельности. «Скажи мне - и я забуду. Покажи мне - и я запомню. Дай мне действовать самому - и я научусь». Эти слова мудрого Конфуция современны как никогда. Конечно, быстрее и легче показать, объяснить, чем позволить ученикам самим открывать знания и способы действий. Самостоятельно ставить цели, анализировать, сопоставлять, оценивать, а главное - не бояться ошибаться в поисках нового пути. Именно этому нужно учить в школе. Решение практико-ориентированных задач на уроках математики должно иметь конкретные цели: 1. Научиться решать задачи, с которыми каждый из нас может столкнуться в повседневной жизни. 2. Опровергнуть мнение, что не всем нужно учиться математике. 3. Доказать, что математика нужна всем, чем бы человек не занимался, какой бы профессией не овладевал, где бы не учился. 4. Готовиться к Единому Государственному Экзамену, в который входят практико-ориентированные задачи. Одной из основных задач, стоящих перед школой, является выяснение многообразных применений школьного курса математики при изучении смежных предметов, в технике, экономике. Приложение 3. Одним из основных путей обеспечения математической грамотности высокого уровня компетентности есть реализация прикладной направленности обучения математике. Без преувеличения можно утверждать, что реализация прикладной направленности обучения математике существенно способствует решению всех основных задач обучения и воспитания молодежи. Главное отличие в конкретизации понятия математической грамотности в указанных исследованиях связано с отличиями между умениями и способностями. Но несмотря на это существенное отличие, толкования понятия математической грамотности имеют одинаковый главный признак – готовность человека применять математику в различных ситуациях, связанных с жизнью. Именно поэтому, задания, призванные исследовать состояние математической грамотности учеников, в подавляющем большинстве имеют четко выраженную прикладную направленность и их решение предусматривает, прежде всего, владение учащимися приемами деятельности прикладного характера. По методикам данных технологий отправляла статьи на следующие порталы: https://infourok.ru/, https://урок.рф/, https://mega-talant.com/, https://my.1sept.ru/, https://pedsovet.org/beta. |
Приложение 1
В своей работе я стараюсь разнообразить домашнее задание – предлагаю план каждому обучающемуся, в зависимости от своих способностей, желаний, самочувствия, выбрать уровень выполнения заданий, темп, тем самым создавая условия свободного выбора. Так повышается интерес к изучению математики, совершенствуются умственные способности. Заметила, что учащиеся очень хорошо, с интересом реагируют на такие домашние задания, серьёзно относятся к их выполнению. Такая форма плана, прежде всего, создает удобства для обучающегося.
Меняется смысл графы «творческие задания». Оно может быть сформулировано, как правило, по желанию ученика или по обоюдному желанию сторон. Задания могут быть направлены на углубленное изучение предмета или на ликвидацию возникших «пробелов» в знаниях ученика.
Ученик имеет ясные представления о целях своей учебной деятельности; осознает мотивы своей учебной деятельности; планирует свою учебную деятельность; оценивает последствия своей учебной деятельности.
ИНДИВИДУАЛЬНЫЙ ПЛАН ДОМАШНЕГО ЗАДАНИЯ ПО ГЕОМЕТРИИ 7 КЛАСС
|
Тема |
Сроки |
Теория |
Практика |
Оценки за виды деятельности учителя |
||||||
|
«3» |
«4» |
«5» |
«3» |
«4» |
«5» |
Теория |
Практика |
Творческое задание |
||
|
Треугольники |
13.11-12.12 |
п.14-23, определение, признаки равенства треугольников |
п.14-23, определение, признаки равенства треугольников, медиана, высота, биссектриса, свойства равнобедренного треугольника |
п.14-23, определение, признаки равенства треугольников, медиана, высота, биссектриса, свойства равнобедренного треугольника, задачи на построение |
№90, 91, 107, 108, 143, 146 Тест№1 |
№96, 109, 124, 137, 146, 156 Тест№1 |
№96, 109, 124, 137, 146, 156, 157 Тест№1 |
|
|
|
|
Творческое задание:
|
||||||||||
Приложение 2
Методика «Взаимотренажа»
Алгоритм работы
1. Получи карточку.
2. Продиктуй напарнику первый вопрос своей карточки.
3. Выслушай ответ напарника
4. Сверь ответ по своей карточке
5. Если ответ правильный продиктуй второй вопрос.
6. Если ответ не правильный, предложи товарищу еще раз ответить на вопрос.
7. Если напарник ошибся несколько раз, скажи ему правильный ответ, а затем переходи к следующему вопросу.
8. Когда проработаешь все вопросы своей карточки, поменяйся с напарником ролями.
9. Выслушай вопросы напарника, ответь на них. Когда все вопросы продиктованы, закончи работу и поменяй напарника
Табло учёта по методике ВТ:
|
|
К-1 |
К-2 |
К-3 |
К-4 |
|
Ученик 1 |
+ |
+ |
+ |
. |
|
Ученик 2 |
+ |
+ |
+ |
+ |
|
Ученик 3 |
+ |
+ |
. |
|
|
Ученик 4 |
+ |
+ |
+ |
+ |
Ученик 1отработал все 6 карточек по методике ВТ и переходит к следующему виду работы. Ученик 2отработал 2 карточки (К-1 и К-2) и работает над К-3.
|
К-1 5 • 3 =15 7 • 5 =35 9 • 3 =27 8 • 6 =48 4 • 4 =16 8 • 9 =72
|
К- 2 2 • 8 =16 9 • 4 =36 5 • 8 =40 6 • 6 =36 8 • 4 =32 7 • 9 =63 |
К – 3 6 • 4 =24 8 • 3 =24 4 • 7 =28 9 • 5 =45 7 • 8 =56 3 • 3 =9
|
К – 4 3 • 2 =6 3 • 4 =12 4 • 8 =32 2 • 2 =4 9 • 6 =54 8 • 5 =40
|
Методика «Взаимообмен заданиями»
Алгоритм работы
1. Объясните партнёру задание 1-ой части своей карточки. Проверьте, как он сделал записи в свою тетрадь.
2. Выслушайте объяснения партнёра по 1-ой части его карточки. Проверьте, как он сделал записи в свою тетрадь.
3. Поменяйтесь карточками и выполните каждый 2-ое задание новой карточки.
4. Сверьте вторые задания.
- если они выполнены одинаково, то поблагодарите друг друга,
- если есть расхождения, то проверьте задания друг друга. Найдите и исправьте ошибки.
Табло учёта по методике ВЗ:
|
|
РН 1 |
РН 2 |
РН 3 |
РН 4 |
РН 5 |
РН 6 |
|
Ученик 1 |
+ |
|
|
|
|
|
|
Ученик 2 |
|
. |
|
|
|
|
|
Ученик 3 |
|
|
++ |
|
|
|
|
Ученик 4 |
|
|
|
+ |
|
|
|
Ученик 5 |
|
|
|
|
++ |
|
|
Ученик 6 |
|
|
|
|
|
. |
Из этой таблицы видно, что Ученик 1 выполнил задание РН1, Ученик 3– РН3, Ученик 5– РН5, Ученик 2 и 6 продолжают работать соответственно над заданиями РН2 и РН6.
«Запуск» раздела считается законченным, если каждое задание раздела выполнено хотя бы одним учеником. Из данной таблицы видно, что «запуск» не осуществлен, т.к. никто не выполнил задания РН2 и РН6. После того, как Ученик 2 выполнит задание РН2, а Ученик 6 РН6, «запуск» будет осуществлен.
Карточка №3. Система двух уравнений с двумя неизвестными. Графический метод решения.
I часть карточки
1. Прочитай карточку
2. Просмотри теоретический материал на стр. 144-145 .
3. Разбери задания № 617 и 618. Разбери теоретический материал на стр. 154-156
4. Сделай упражнения №№ 644 (2,4), 645 (2,4), 647, 648
5. Проверь упражнения
II часть карточки
6. Выполни задания №№ 650, 651
7. Объясни партнёру упражнения №№ 644, 645, 647,648
8. Выслушай теоретический материал из карточки партнера
9. Задай по прослушанному материалу вопросы
10. Обменяйся карточками с партнёром.
Методика« Взаимообмен тем»
Алгоритм работы
1. Получите задания и темы к нему
2. Прочтите и разберите основные понятия.
3. Выпишите формулировки теоремы.
4. Сделайте чертёж, разберите доказательства по учебнику.
5. Сделать себе краткий план доказательства.
6. Разобрать следствия, выписать формулировки, сделать чертежи.
7. Подумайте, как будете доказывать факты вашему партнёру, какие могут быть вопросы, как вы ответите на них.
8. Придумайте вопросы партнёру.
9. Сделайте задачу 1-го уровня
10. Сделайте задачу второго уровня.
Методика« Взаимопроверки индивидуальных заданий»
Алгоритм работы
Методика взаимопроверки индивидуальных заданий предназначена для закрепления и повторения изученных тем. В отличие от тренировки, предметом проверки является не собственно ответ. А логика и содержание действий по решению задачи, вопроса. За счёт проговаривания ученик приходит к осознанию выполняемого им способа действия, а это лежит в основе формирования устойчивых навыков.
1. Самостоятельно выполните все задания своей карточки.
2. Найдите себе напарника для проверки первого задания своей карточки.
3. Работа в паре.
• Восстанови напарнику (если нужно, на черновике) ход выполнения своего первого задания.
• Выслушайте отношение напарника по поводу выполнения вами задания. Ответьте на его вопросы и исправьте замеченные ошибки.
• Выслушайте своего напарника. Проследите правильность его действий. Задайте вопросы по поводу замеченных ошибок. Попросите исправить ошибки.
• Поблагодарите друг друга за работу.
4. Для проверки своего следующего задания найдите себе другого напарника. Работайте, как указано в п.З.
5. Как только вы проверите с разными партнерами все вопросы и задания своей карточки, возьмите у командира сводного отряда следующую карточку и поработайте с ней так же, как в пунктах 1-3.
Чтобы хорошо работала пара, надо у учащихся формировать навыки социального и психологического плана:
· общаться в паре, не мешая другим участникам учебной группы;
· слушать друг друга, не перебивая без особой надобности;
· слышать друг друга, то есть понимать услышанное;
· считаться с мнением партнёра, уважать это мнение;
· отстаивать свою точку зрения;
· быть терпимым к своему собеседнику;
· давать оценку своим действиям и действиям других;
· чувствовать ответственность за порученное дело.
Табло учёта по методике ВПЗ:
|
ФИ |
ИЗ1 |
ИЗ2 |
ИЗ3 |
ИЗ4 |
ИЗ5 |
ИЗ6 |
ИЗ7 |
ИЗ8 |
ИЗ9 |
|
Ученик 1 |
+ |
|
|
|
|
|
. |
|
|
|
Ученик 2 |
|
+ |
|
|
|
|
|
. |
|
|
Ученик 3 |
|
|
+ |
|
|
|
|
|
|
|
Ученик 4 |
|
|
|
+ |
|
. |
|
|
|
|
Ученик 5 |
|
|
|
|
+ |
|
|
|
|
|
Ученик 6 |
|
|
|
|
|
+ |
|
|
. |
Натуральные числа.
К-1
1.Выполните действия:
105+64:8-56; (560:35+45)*43;
2.Решить уравнения:
4*х=126 144 : у=12
х+125=775 у-143=42
К-2
1.Выполните действия:
245+750:25-100 (1872:52-36)*21
2.Решить уравнения:
5*х=165 5940:у=45
25+х=745 314-у=24
Ребята работают в парах сменного состава по методике «Взаимотренажа», отрабатывают вычислительные навыки.
Приложение 3
Компетентностно-ориентированные задания
Первый уровень – уровень воспроизведения. Первый уровень включает воспроизведение математических фактов, методов и выполнение вычислений. Учащиеся могут применять базовые математические знания в стандартных, четко сформулированных ситуациях. Например:
Задача 1.
После 7 стирок кусок хозяйственного мыла уменьшился вдвое по длине, ширине и высоте. На сколько стирок его еще хватит? (Тема: «Объем параллелепипеда», 11 класс).
Второй уровень (уровень установления связей) включает установление связей и интеграцию материала из разных математических тем, необходимых для решения поставленной задачи. Учащиеся могут применять свои знания в разнообразных, достаточно сложных ситуациях. Они могут упорядочивать, соотносить и производить вычисления, решать многошаговые текстовые задачи. Учащиеся могут выполнять несложные алгебраические задания, включающие составление выражений, решение систем линейных уравнений, определять значения величин, используя известные формулы. Они могут интерпретировать информацию, представленную в таблицах и на графиках.
Например:
Температура воздуха изменялась в течение дня от 7° до 26° Цельсия (дается график изменения температуры). Изобразите график функции, на котором будет изображена температура воздуха в градусах по фаренгейту, соответствующая температуре на графике.
Третий уровень (уровень рассуждения) – математические размышления, требующие обобщения и интуиции. Учащиеся могут организовывать информацию, делать обобщения, решать нестандартные проблемы, делать выводы на основе исходных данных и обосновывать их. Он могут вычислить изменения имеющихся данных, связанные с процентами, применят знания алгебраических понятий и зависимостей, составить алгебраическую модель несложной ситуации. Они могут интерпретировать, интерпонировать данные в различных таблицах и на графиках. В заданиях третьего уровня, прежде всего, необходимо самостоятельно выделить в ситуации проблему, которая решается средствам математики и разработать соответствующую ей математическую модель. Решить поставленную задачу, используя математические рассуждения и обобщения и интерпретировать решение с учетом особенностей рассмотренной в задании ситуации.
Например:
У садовника имеется 32 метра провода, которым он хочет обозначить на земле границу клумбы. Форму клумбы ему надо выбрать из следующих вариантов.
 |
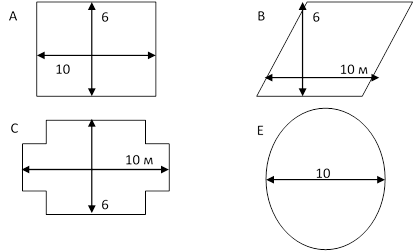Обведите слово «Да» или «Нет» в таблице около каждой формы клумбы в зависимости от того, хватит или не хватит садовнику 32м провода, чтобы обозначить ее границу.
|
Форма клумбы |
Хватит ли 32 м провода, чтобы обозначить границу клумбы |
|
Форма А |
Да\Нет |
|
Форма В |
Да\Нет |
|
Форма С |
Да\Нет |
|
Форма Е |
Да\Нет |
Модель – схема
Компетентностно-ориентированного задания
· Название задания
· Аспекты формируемых ключевых компетенций
· Стимул (если …, то …)
· Личностно-значимый познавательный вопрос (задачная формулировка)
· Источник информации по данному вопросу (текст, таблица, график, статистические данные, т.п.)
· Задания (вопросы) по работе по данной информации
· Бланк для выполнения задания (если оно подразумевает структурированный ответ)
· Модельный ответ
· Инструмент проверки (оценочный бланк, ключ)
Стимул мотивирует ученика на выполнение задания, включает описание ситуации или другие условия задачи, которые играют роль источника информации:
– мотивирует учащегося на выполнение задания;
– моделирует практическую, жизненную ситуацию;
– при необходимости может нести функцию источника информации.
Стимул должен:
– быть кратким (не более трех предложений)
– не отвлекать учащегося от содержания задания.
Задачная формулировка понимается однозначно, четко соотносится с модельным ответом (шкалой), соответствует возрасту учащегося, интересна учащемуся. (Мы не можем проверять то, что не требовали в задачной формулировке. Мы обязаны проверять то, что предписывали в задачной формулировке).
Источник информации содержит информацию, необходимую для успешной деятельности учащегося по выполнению задания. (Необходим и достаточен для выполнения заданной деятельности, интересен, соответствует возрасту учащихся). На одном источнике (наборе источников) может строиться несколько заданий. Учащийся не должен быть знаком с источником до выполнения задания.
Бланк задает структуру предъявления учащимся результата своей деятельности по выполнению задания.
Инструмент проверки определяет количество баллов за каждый этап деятельности и общий итог в зависимости от сложности учебного материала, дополнительных видов деятельности.
Инструментом проверки может быть:
· Ключи для тестовых заданий закрытого типа.
· Модельный ответ обычно используется для открытых тестовых заданий с кратким ответом.
· Аналитическая шкала используется для открытых тестовых заданий с развернутым ответом.
· Бланк наблюдений за групповой работой используется для оценки вклада каждого участника в групповой продукт и эффективности деятельности всей группы в целом.
Практико-ориентированные задачи
Я хочу представить вашему вниманию три группы практико-ориентированных задач.
1 группа-это задачи профориентационного направления
|
Профессия |
Задачи |
|
Домохозяйка
|
1. Мама решила приготовить салат из огурцов, помидоров и редиски. Вся масса салата должна составить 400 г. Сколько нужно положить помидоров, если масса огурцов составляет 150 г., а масса редиски в 2 раза меньше массы огурцов? 2. Хозяйка собрала 17 кг яблок. Сколько получится свежевыжатого сока, если сок составляет 80% от массы всех яблок? 3. Купили 15 кг груш. На компот решили истратить 40% все груш, а остальное пошло на варенье. Сколько кг сахара нужно купить для варенья, если на 1 кг свежих груш нужно 800 г. сахара? |
|
Повар-кондитер |
1. Для приготовления летнего салата для семьи нужно 500г помидоров по цене 25 руб. за 1 кг, 300 г огурцов по цене 40 руб. , 30 г зеленого лука по цене 6 руб., 50 г сметаны по цене 50 руб. за баночку массой 200 г. Какова будет стоимость салата? 2. На шоколадную фабрику привезли 2 ящика какао бобов. В первом ящике было в 10,5 раз больше какао бобов чем во втором. После того как из первого ящика взяли 16 кг, а во второй добавили 22 кг, какао бобов стало поровну. Сколько какао бобов было первоначально в каждом ящике. |
|
Продавец |
1. В магазин привезли 400 кг апельсинов. В первый день продали 15%, а во второй день 0,5 оставшихся. Сколько осталось апельсинов в магазине? 2. В школьный буфет привезли пирожки. Ученики старших классов скупили 120 пирожков, что составило 48% всего количества. Сколько всего привезли пирожков? Сколько пирожков купили ученики младших классов, если 17 пирожков остались не проданными? |
|
Водитель |
Водителю выдали американский автомобиль, на спидометре которого скорость измеряется в милях в час. Какова скорость автомобиля в километрах в час, если спидометр показывает 26 мили/час? Ответ округлить до целого числа. Американская миля равна 1609 м. |
|
Воспитатель |
В летнем лагере 245 детей и 29 воспитателей. В автобус помещается не более 46 пассажиров. Сколько автобусов требуется, чтобы перевезти всех из лагеря в город? |
2 группа - геометрические задачи, связанные с жизнью, с практической деятельностью человека.
1. На берегу реки требуется построить водонапорную башню для снабжения водой двух сел так, чтобы общая длина труб от водонапорной башни до обоих сел была наименьшей.
3 группа – задачи семейно-практического содержания. Например, «один день из жизни семьи»
1. Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза в день в течение 8 дней. В одной упаковке 10 таблеток лекарства по 0,25 г. Какого наименьшего количества упаковок хватит на весь курс лечения?
2. Для ремонта квартиры купили 42 рулона обоев. Сколько пачек обойного клея нужно купить, если одна пачка клея рассчитана на 8 рулонов?
Практико-ориентированные задачи использую на различных этапах урока.
Скачано с www.znanio.ru
Информационная карта инновационного педагогического опыта /практики/
Актуальность В связи с тем, что школьники в международных исследованиях показывают низкий уровень математической грамотности перед учителями встала проблема в повышении данного показателя с помощью…
Третий – математические размышления, требующие обобщения и интуиции
Математическая грамотность – способность человека определять и понимать роль математики в мире, в котором он живет, высказывать хорошо обоснованные математические суждения и использовать математику так,…
Формирование ключевых компетентностей посредством задач позволяет реализовать компетентностный подход на уроках математики как средство повышения математической грамотности учащихся
КСО. На первом этапе это лучше делать в парной организационной форме, причем начинать с пар постоянного состава
Компетентностные задачи составлены так, что имеют проблемный характер и требуют применения знаний из разных разделов одной предметной области (математика) или из разных предметных областей, или…
Описание инновационного опыта (размещение как приложение в формате статьи) «Математическая грамотность – способность человека определять и понимать роль математики в мире, в котором он живет,…
Приложение 1 В своей работе я стараюсь разнообразить домашнее задание – предлагаю план каждому обучающемуся, в зависимости от своих способностей, желаний, самочувствия, выбрать уровень выполнения…
Творческое задание: Составить по теме
К-1 5 • 3 = 15 7 • 5 = 35 9 • 3 = 27 8 • 6 = 48 4 • 4 =…
II часть карточки 1.
Выслушайте отношение напарника по поводу выполнения вами задания
К-2 1.Выполните действия: 245+750:25-100 (1872:52-36)*21 2
Приложение 3 Компетентностно-ориентированные задания
Обведите слово «Да» или «Нет» в таблице около каждой формы клумбы в зависимости от того, хватит или не хватит садовнику 32м провода, чтобы обозначить ее…
Стимул должен: – быть кратким (не более трех предложений) – не отвлекать учащегося от содержания задания
Повар-кондитер 1. Для приготовления летнего салата для семьи нужно 500г помидоров по цене 25 руб
© ООО «Знанио»
С вами с 2009 года.
