
Публикация является частью публикации:
Выступление на школьной научно-практической конференции 2017 года.
Учитель математики МАОУ СОШ № 10 Пирогова Татьяна Николаевна.
Формирование навыков смыслового чтения и устной математической речи.
Как установили ученые, на успеваемость ученика влияет около 200 факторов.
Фактор №1 – это навык чтения, который гораздо сильнее влияет на успеваемость, чем все вместе взятые.
(Слайд 2).Сегодня чтение, наряду с письмом и владением компьютером, относится к базовым умениям, которые позволяют продуктивно работать и свободно общаться с разными людьми. Чтение является универсальным навыком: это то, чему учат, и то, посредством чего учатся.
(Слайд 3). Смысловое чтение – вид чтения, которое нацелено на понимание читающим смыслового содержания текста. Для смыслового понимания недостаточно просто прочесть текст, необходимо дать оценку информации, откликнуться на содержание. Смысловое чтение является метапредметным результатом освоения образовательной программы основного общего образования, а также является универсальным учебным действием
(Слайд 4). Международная программа по оценке образовательных достижений учащихся PISA 2012 года показала весьма неутешительные для России результаты
Обеспечивая учащихся значительным багажом предметных знаний, российская система образования не способствует развитию у них умения выходить за пределы учебных ситуаций, в которых формируются эти знания, и решать творческие задачи.
(Слайд 5). Например, один из выпускников при решении задачи из текстов ЕГЭ дал совершенно неправильный ответ: «394».
Вывод очевиден. Этот ученик не умеет работать с текстом задачи. Он невнимательно читает условие, не может отделить условие задачи от вопроса, не умеет критически оценить полученный результат. Если бы этого ученика научили при чтении задачи выделять, подчёркивать ключевые данные, чтобы зафиксировать в сознании информацию, а при проверке решения подставить полученный результат в текст вопроса, то подобной ошибки он бы не сделал.
(Слайд 6). Одно из заданий PISA звучало так: «В телепередаче журналист показал диаграмму и сказал, что в 1999 году по сравнению с 1998-м резко возросло число ограблений. Считаете ли вы, что журналист сделал правильный вывод?»
Нужный ответ — «нет, такой вывод сделать нельзя». Его дали лишь 3% (!) россиян. Ученики «купились» на наглядность диаграммы – видно, что правый столбик выше левого! Но при этом не учли, что число ограблений увеличилось за год всего на 8 (1,5%), что нельзя считать резким ростом.
(Слайд 7). Важнейшее общеучебное действие – это смысловое чтение:
• извлечение информации; определение основной и второстепенной информации;
• построение речевых высказываний, адекватно, осознанно и произвольно передающих содержание текста, дающих ответ на вопрос;
• логические действия, направленные на анализ, обобщение, классификацию, рассуждения и умозаключения на основе прочитанного текста.
(Слайд 8). Математические тексты имеют свои особенности.
Развитие математической грамотности учащихся напрямую связано с развитием навыков смыслового и функционального чтения.
(Слайд 9). Чтобы справиться с решением задачи, учащиеся должны:
- осмысленно читать и воспринимать на слух текст задания;
- уметь извлекать и анализировать информацию, полученную из текста;
- уметь критически оценивать данную информацию;
- уметь читать таблицы, диаграммы, схемы, условные обозначения.
(Слайд 10). К ключевым направлениям формирования умений работы с текстом относят следующие:
5 – 6 классы
· выделение главного в тексте;
· составление примеров, аналогичных приведенным в тексте;
· умение найти в тексте ответ на поставленный вопрос;
· грамотно пересказать прочитанный текст.
(Слайд 11). 7 – 8 классы
· умение составить план прочитанного;
· воспроизводить текст по предложенному плану;
· умение пользоваться образцами решения задач;
· запоминание определений, формул, теорем.
9 – 11 классы
· работа с иллюстрациями (рисунками, чертежами, диаграммами);
· использование новой теории в различных учебных и жизненных ситуациях;
· подтверждение научных фактов;
· конспектирование новой темы.
(Слайд 12). Книга Н.Н. Сметанниковой «Обучение стратегиям чтения в 5-9 классах: как реализовать ФГОС» М: Баласс, 2011 – основной помощник учителя, так как в ней даны чёткие рекомендации и приёмы смыслового чтения. В научной литературе «стратегии смыслового чтения» понимаются как различные комбинации приемов, которые используют учащиеся для восприятия графически оформленной текстовой информации и ее переработки в личностно-смысловые установки в соответствии с коммуникативно-познавательной задачей.
(Слайд 13). 1. Приём «Тонкие» и « толстые» вопросы.
Вопросы такого
плана возникают на протяжении всего урока математики. А можно учащимся
предложить задание: составьте вопросы по теме, по тексту параграфа и т.д.
«Тонкие» вопросы – вопросы, требующие простого, односложного ответа; «толстые»
вопросы – вопросы, требующие подробного, развёрнутого ответа.
Стратегия позволяет формировать умение формулировать вопросы и умение
соотносить понятия. После изучения темы учащимся предлагается сформулировать по
три «тонких» и три «толстых» вопроса, связанных с пройденным материалом. Затем
они опрашивают друг друга, используя таблицы «толстых» и «тонких»
вопросов.
(Слайд 14). 2. Приём «Составление краткой записи задачи»
Формируется умение целенаправленно читать учебный текст, задавать проблемные вопросы, вести обсуждение в группе.
(Слайд 14). 3. Приём «Составление вопросов к задаче»
Анализ информации, представленной в объёмном тексте математической задачи, формулировка вопросов к задаче, для ответа на которые нужно использовать все имеющиеся данные; останутся не использованные данные; нужны дополнительные данные.
(Слайд 15). 4. Приём «Вопросы к тексту учебника»
Стратегия позволяет формировать умение самостоятельно работать с печатной информацией, формулировать вопросы, работать в парах и в группах.
(Слайд 16). 5. Приём «Учимся задавать
вопросы раз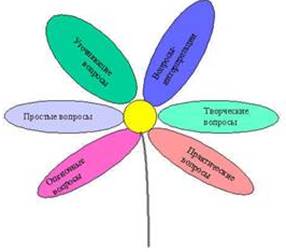 ных типов» – « Ромашка Блума»
ных типов» – « Ромашка Блума»
Шесть
лепестков – шесть типов вопросов.
Простые вопросы. Отвечая на них, нужно назвать какие-то факты,
вспомнить, воспроизвести некую информацию. Применяю на традиционных формах
контроля: на зачетах, при использовании терминологических диктантов и т.д.
Уточняющие вопросы. Обычно начинаются со слов: «То есть ты говоришь, что...?», «Если я правильно поняла, то...?», «Я могу ошибаться, но, по-моему, вы сказали о...?». Целью этих вопросов является предоставление обратной связи ученику относительно того, что он только что сказал. Очень важно эти вопросы задавать без негативной мимики.
Интерпретационные (объясняющие) вопросы. Обычно начинаются со слова «Почему?». В некоторых ситуациях (как об этом говорилось выше) могут восприниматься негативно – как принуждение к оправданию. В других случаях – направлены на установление причинно-следственных связей. Если учащийся знает ответ на этот вопрос, тогда он из интерпретационного «превращается» в простой. Следовательно, данный тип вопроса «срабатывает» тогда, когда в ответе на него присутствует элемент самостоятельности.
Творческие вопросы. Когда в вопросе есть частица «бы», а в его формулировке есть элементы условности, предположения, фантазии прогноза. «Что бы изменилось в…, если бы…?», «Как вы думаете, как будет…?».
Оценочные вопросы. Эти вопросы направлены на выяснение критериев оценки тех или фактов. «Чем … отличается от …?» и т.д.
Практические вопросы. Это вопросы, направленные на установление взаимосвязи между теорией и практикой. Например: «Где вы в обычной жизни вы могли наблюдать симметрию?».
(Слайд 17).6. Приём «Чтение с остановками»
Суть данного приема заключается в том, чтобы побудить учащихся размышлять. Чтение с остановками помогает правильно понять условие, составить краткую запись, у ученика рождается план решения задачи. При прочтении текста можно использовать цвета или подчеркивание.
(Слайд 17).7. Приём «Инсерт»
Прием «Инсерт» – это маркировка текста по мере его чтения.
Применяется для стимулирования более внимательного чтения. Чтение превращается в увлекательное путешествие.
1. Чтение индивидуальное.
Читая, ученик делает пометки в тексте:
V – уже знал;
+ – новое;
– – думал иначе;
? – не понял, есть вопросы.
2. Читая, второй раз, заполняют таблицу, систематизируя материал.
Записи делают краткие, ключевые слова, фразы. Заполнив таблицу, учащиеся будут иметь мини-конспект. После заполнения учащимися таблицы обобщаем результаты работы в режиме беседы. Этот приём способствует развитию умения классифицировать, систематизировать поступающую информацию, выделять новое.
(Слайд 18).8. Приём «Кластер»
Кластеры используют для структуризации и систематизации материала. Кластер – способ графической организации учебного материала, суть которой заключается в том, что в середине листа записывается или зарисовывается основное слово (идея, тема), а по сторонам от него фиксируются идеи (слова, рисунки), с ним связанные.
Предлагается прочитать изучаемый материал и вокруг основного слова (тема урока) выписать ключевые, по их мнению понятия, выражения, формулы. А затем вместе в ходе беседы или ребята работая в парах, группах наполняют эти ключевые понятия, выражения, формулы необходимой информацией.
(Слайд 19).9. Приём «Ключевые слова»
Это слова, по которым можно составить рассказ или определения некоторого понятия.
(Слайд 20).10. Приём «Верные и неверные утверждения»
Универсальный
прием, способствующий актуализации знаний учащихся и активизации мыслительной
деятельности. Данный прием дает возможность быстро включить детей в
мыслительную деятельность и логично перейти к изучению темы урока.
Стратегия формирует умение оценивать ситуацию или факты, умение анализировать
информацию, умение отражать свое мнение. Детям предлагается выразить свое
отношение к ряду утверждений по правилу: верно – «+», не верно – «-».
(Слайд 21).11. Приём «Верите ли вы…»
Проводится с целью вызвать интерес к изучению темы и создать положительную мотивацию самостоятельного изучения текста по этой теме.
Проводится в начале урока, после сообщения темы.
(Слайд 22-23).12. Приём «Синквейн»
Развивает умение учащихся выделять ключевые понятия в прочитанном, главные идеи, синтезировать полученные знания и проявлять творческие способности. Структура синквейна:
Существительное (тема).
Два прилагательных (описание).
Три глагола (действие).
Фраза из четырех слов (описание).
Существительное (перефразировка темы).
Данные приемы не только помогают учащимся работать с информационным или художественным текстом, но и зримо демонстрируют процесс продвижения от незнания к знанию, делают процесс чтения более осмысленным, помогают выделять основные аспекты в изучаемой информации, формируют умение графически представлять результат работы с текстом.
(Слайд 24). Когда ребенок владеет смысловым чтением, то у него развивается устная речь и, как следующая важная ступень развития, речь письменная. «Знаю, но не умею объяснить» - говорят многие учащихся.
Развитие речи - это повседневная работа над речью на всех уроках. Труднее это дается на уроках математики. Если в разговорной речи мы оперируем общеупотребляемыми терминами, то на уроках математики в основном только терминами математики, причем, некоторые из них мы в обыденной жизни не употребляем (гомотетия, дифференцирование и т.п.). Поэтому, для развития математической речи нужна специальная и кропотливая работа
(Слайд 25). 1. Работа над звуковой стороной речи, которая сводится к формированию правильного произношения и выразительного чтения математических терминов и выразительного чтения любого задания.
2. Словарная работа, которая сводится к пониманию и умению объяснять значение математических терминов, усвоению их правильного написания и формированию умений составлять содержательное, связное высказывание.
3. Формирование культуры математической речи, которое сводится к устранению грамматических и математических ошибок, употребления «лишних» слов, неправильного порядка слов в предложении.
4. Развитие связной математической речи, которое сводится к умению строить связные математические высказывания, логические объяснения.
(Слайд 26). В своей работе с целью развития математической грамотности и культуры речи мы применяем следующие виды работ:
1. Математический диктант (задания по переходу от словесной записи к символической и обратно; запись математического термина по его лексическому значению, например «Сторона прямоугольного треугольника, лежащая напротив прямого угла … ).
2. Словарный диктант (правильное написание математических терминов).
3. Формулировка определений и теорем, доказательство теорем.
4. Устная работа (устные ответы обучающихся).
5. Решение задач с комментированием своего ответа.
6. Оценивание и комментирование чужого ответа.
7. Работа в парах, группах (совместный поиск решения проблемы, обоснование, вывод).
8. Сообщение (выступление с докладом по теме урока).
9. Составление и отгадывание кроссвордов и загадок по пройденной теме,
10. придумывание историй, сказок, написание стихотворений.
Рассмотренные приёмы работы обеспечивают не только усвоение учебного материала, но и активизируют умственную деятельность учащихся, прививают интерес к изучаемому предмету. Таким образом, эффективность процесса обучения зависит от умения правильно выбрать технологические приёмы, удачно комбинировать их, вмещать их в рамки уже знакомых традиционных форм урока.
(Слайд 27). Спасибо за внимание!
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.