Фрагменты уроков по теме «Решение уравнений» в 6 классе.

Основы работы с уравнениями закладываются, объясняются на простых математических объектах, пока предмет еще не разделен на алгебру и геометрию. Именно в этом возрасте ребенку отводится время на формирование представление о том, как изучаемый объект устроен и как он используется в реальных ситуациях. Исключение этого важного этапа математической подготовки в большинстве случаев оказывается впоследствии невосполнимым. Даже опытный учитель, работая с учеником старших классов, не сможет в полной мере компенсировать недостаток внимания к уравнениям в младших классах. Можно только дать представление о методах решения или натаскать на заучивание определенных алгоритмов.

В данной статье рассматриваются фрагменты уроков, которые позволят заинтересовать детей к изучению темы и понять принципы решения различных уравнений.

Очень важным этапом урока является мотивация к изучению темы. И в этом плане большой интерес вызывают исторические задачи, задачи в литературе, в стихах, задачи, имеющие практическое применение. 

Мотивация к учебной деятельности.

Задача 1. Античные ученые часто составляли задачи в стихотворной форме. Вот пример – древнеиндийская задача:

«Есть кадамба-цветок.

На один лепесток

Пчелок пятая часть опустилась.

Рядом тут же росла

Вся в цвету сименгда,

И на ней третья часть поместилась.

Разность их ты найди,

Ее трижды сложи,

На кутай этих пчел посади.

Лишь одна не нашла

Себе места нигде,

Все летала то взад, то вперед и везде Ароматом цветом наслаждалась.

Назови теперь мне, подсчитавши в уме, Сколько пчелок всего здесь собралось?»

При решении составляется уравнение: .

(Ответ: 15 пчел)

Задача 2. Известный ученый Диофант жил в III веке, остальные известные факты его биографии описаны в таком стихотворении – загадке.

Говорят, что оно выгравировано на его надгробии [4]:

«Путник! Здесь прах погребен Диофанта,

И числа поведать могут, о чудо, сколь долг был век его жизни.

Часть шестую его представляло счастливое детство. Двенадцатая часть протекла еще жизни – Пухом покрылся тогда подбородок.

Седьмую в бездетном браке провел Диофант.

Прошло пятилетье.

Он был осчастливлен рожденьем прекрасного первенца сына, Коему рок половину лишь жизни счастливой и светлой Дал на земле по сравненью с отцом.

И в печали глубокой старец земного удела конец воспринял, Переживши года четыре с тех пор, как сына лишился.

Скажи, скольких лет жизни достигнув, Смерть воспринял Диофант?»

В решении составляется такое уравнение: .

(Ответ: 84 года)

Задача 3. Древний кирпич, называвшийся плинфа, имел совсем не такие размеры, как современный. Ширина плинфы составляет 0,75 от ее длины. Высота – на 26,5 см меньше ширины. Вычислите размеры плинфы, если известно, что ее длина и высота в сумме равны 43,5 см [3].

Составляем уравнение: .

(Ответ: длина - 40 см, ширина - 30 см, высота - 13,5 см)

Формирование навыка решения уравнений, в которых переменная находится в обеих частях

Решим задачу. Задача 1. Сейчас отцу 34 года, а сыну 11 лет.  Через сколько лет возраст отца будет в 2 раза больше возраста сына? 

Решение:  Пусть через  лет отец будет в два раза старше сына.

                                                                      Сейчас                       Будет через x лет

                          Отец                                     34                                    

                           Сын                                     11                                    

Составим уравнение:  

Решаем уравнение:

;

–      Что мы получили? Что не так в этом уравнении?

(Неизвестные находятся в обеих частях равенства)

–      Получаем, что неизвестное находится в обеих частях уравнения. Как же быть в таком случае?

(Ученики предлагают варианты решения)

–      Чтобы решить такое уравнение, воспользуемся следующим правилом:

«Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части в другую, изменив при этом его знак».

Т.е. нам надо сделать так, чтобы все неизвестные слагаемые были в одной части, а известные – в другой. 

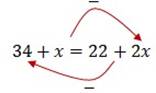
Для удобства поменяем выражения местами.

Приведем подобные слагаемые.

.

Ответ: 12

Далее предлагается       самостоятельно   решить       следующую         задачу, рассуждая на каждом этапе.

Задача 2. На первой стоянке в 4 раза меньше автомашин, чем на второй. После того как на первую приехали 35 автомашин, а со второй уехали 25 автомашин, автомашин на стоянках стало поровну. Сколько автомашин было на каждой стоянке первоначально [1]. 

Решение:

                                                               Первоначально                         Стало

            Первая стоянка                                                                             

             Вторая стоянка                                                                            

Составим уравнение:  

Решаем уравнение:

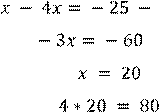
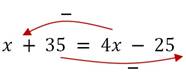
Ответ: на первой стоянке было 20 машин, на второй – 80.

Устная работа.

Задача 3.  Аня получила на уроке оценку. В качестве ответа, на вопрос Сони об отметке, она использовала задачу. Если к полученной оценке прибавить 27 и полученную сумму разделить на 4, то получится 8. Найдите ошибки, которые допустила в решении Соня, и помогите ей узнать, какую оценку получила Аня.

Решение Сони: обозначим за  оценку, которую получила Аня на уроке.

Составим и решим уравнение по условию задачи.

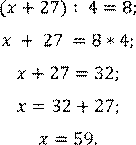
Получилось, что на уроке Аня получила оценку «59».

Правильное решение: ошибка возникла при решении самого уравнения. Соня забыла поменять знак на противоположный при перенесении слагаемого 27.

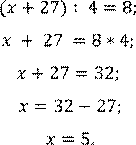
Следовательно, Аня на уроке получила оценку «5».

Ответ: оценка «5».

Чтобы интереснее и легче было запомнить правило переноса слагаемых, можно использовать такое выражение: «При переезде через государственную границу человек меняет свой паспорт, а слагаемое меняет свой знак».

После того, как обучающиеся усвоили правило переноса слагаемых, можно усложнить уравнения, добавив в него скобки, а также дроби.

Задание по парам. Решите уравнения, используя ход решения на карточках [1, 2].

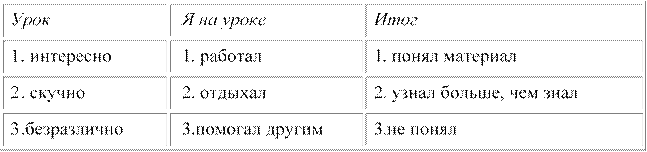
Рефлексия.

«Для меня сегодняшний урок…»

Учащимся дается индивидуальная карточка, в которой нужно подчеркнуть фразы, характеризующие работу ученика на уроке по трем направлениям.

Список литературы:

1.                     Выговская В.В. Поурочные разработки по математике. 6 класс. – 2-е изд. – М.: ВАКО, 2014. – 496 с.

2.                     Ерина Т.М. Рабочая тетрадь по математике: 6 класс: к учебнику Н. Я. Виленкина и др. «Математика: 6 класс». ФГОС – 16-е изд., М.: Издательство «Экзамен», 2017. – 205 с.

3.                     Крижановский А.Ф. Математические кружки. 5–7 классы. –

М.:ИЛЕКСА, 2016. – 320 с.

4.                     http://library.narfu.ru/rus/TRResources/VirtualExhibitions/Pages/2016

0315_matematika_i_literatura.aspx  Математика в литературе.