Интегрированный урок математики и информатики на тему "Арифметическая и геометрическая прогрессии. QBasic" (9 класс)

Урок по алгебре в 9 классе

(с применением компьютеров)

Тема: Арифметическая и геометрическая прогрессии.

Цели:

Ø  закрепление знаний и умений учащихся по данным темам;

Ø  ознакомление учащихся с методом нахождения суммы бесконечной геометрической прогрессии с помощью компьютера;

Ø  вспомнить язык программирования QuickBasic;

Ø  воспитание математической культуры учащихся.

Оборудование: раздаточный материал, компьютеры, телевизор, DVD-плеер.

План урока

         I.    Организационный момент.

       II.    Проверка теоретического материала.

     III.    Устная работа.

     IV.    Решение упражнений.

      V.    Решение задачи на компьютере.

     VI.    Подведение итогов.

   VII.    Домашнее задание.

 VIII.    Решение задач на сообразительность.

Ход урока

I.           Организационный момент.

Сообщение темы и целей урока.

Учитель.

Цель нашего урока:

·        обобщить и упорядочить знания, которые вы получили при изучении арифметической и геометрической прогрессии;

·        познакомимся с рядами;

·        наглядно рассмотрим сходящиеся и расходящиеся ряды;

·        найдем сумму бесконечной геометрической прогрессии с помощью компьютера без соответствующей формулы;

·        и если останется время, решим задачи на сообразительность.

II.        Проверка теоретического материала.

Учитель.

1.     Сформулируйте определение арифметической прогрессии.

2.     Сформулируйте определение геометрической прогрессии.

Далее у ребят имеются листочки с таблицей, которые необходимо заполнить. Первый и второй вариант даются сильным учащимся, третий и четвертый дается слабым учащимся. На обратной стороне доски выполнена верная запись формул.

Вариант 1

Вариант 2

Вариант 3

Вариант 4

Через 5 - 6 минут учащиеся меняются листочками, учитель переворачивает доску, и они сами оценивают друг друга. Кратко анализируются ошибки.

III.       Устная работа.

Задание 1

1.     Найдите разность арифметической прогрессии (а_n): 2; 4; 6; … .

2.     Является ли арифметической прогрессией последовательность, заданная формулой a_n=3n + 1. Если да, то найдите ее третий член.

3.     Найдите разность и четвертый член арифметической прогрессии: 19; 15;… .

4.     Является ли последовательность (b_n) геометрической  прогрессией, если да, то найдите ее знаменатель (b_n): 3; 3; 3; … .

5.     В геометрической прогрессии первый член равен 8, второй 4. Найдите знаменатель.

6.     Является ли последовательность, заданная формулой , геометрической прогрессией. Если является, то найдите знаменатель.

7.     Какой прогрессией является последовательность   Найдите сумму геометрической прогрессии.

8.     Найдите третий член геометрической прогрессии; если b₁ = 6; q = 2.

Задание 2

Найдите сумму геометрической прогрессии 12; -4; ; … Ответ: 9.

Учитель.

1.     Какой прогрессией является данная последовательность?

2.     Чему равен знаменатель?

3.     Убывающей или возрастающей является данная последовательность?

4.     По какой формуле можно найти сумму бесконечной геометрической прогрессии?

Учитель.

Бесконечная геометрическая прогрессия представляет собой последовательность, которая изучается в высшей математике и называется там рядами. Они бывают сходящиеся и расходящиеся. Ряды сходятся, если при неограниченном увеличении номера члены прогрессии стремятся к одному и тому же числу. Ряды расходятся, если при неограниченном увеличении номера члены разница между членами прогрессии увеличивается. Для того чтобы определить сходимость рядов используют признаки сходимости, они в школе не изучаются. Для того, чтобы представить себе, что такое сходимость и расходимость, мы рассмотрим графики функций на телевизоре, которые заданы формулами n-х членов геометрических прогрессий. На графиках вы быстро определите сходится данный ряд или нет.

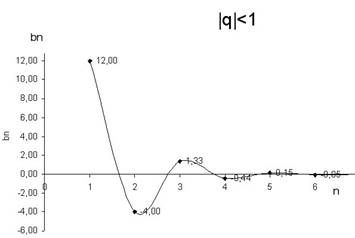
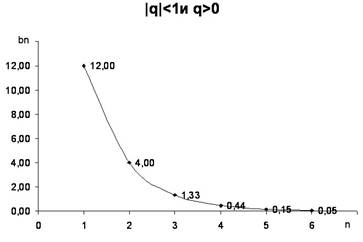
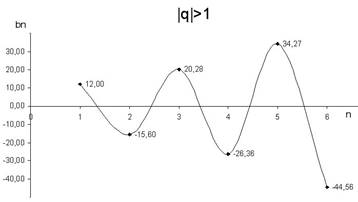
IV.      Решение письменных упражнений.

Трое слабых учащихся выполняют задания на карточках. Остальные выполняют задания в тетрадях и на доске.

Карточка 1

1.     В геометрической прогрессии (b) b=3, q=2. Найдите b₇.

2.     Найдите сумму первых десяти членов арифметической прогрессии (a), если a=5; d=3.

Карточка 2

1.     Найдите первый член геометрической прогрессии (b), b=3; q=3.

2.     В арифметической прогрессии (a) a=-8; d=4. Найдите a.

Карточка 3

1.     Найдите сумму четырех первых членов геометрической прогрессии (b), если b=4; q=3.

2.     Найдите первый член арифметической прогрессии  (a), если a=22; d=2.

Задания для остальных

1)    Найдите первый член, разность и сумму первых четырех членов арифметической прогрессии (a_n), если a₅ = 27; a₂₇ = 60.

2)    Найдите знаменатель геометрической прогрессии (b_n) и сумму четырех первых членов, если b₂ =6; b₄ = 24.

V. Решение задачи на компьютере.

Найдите сумму геометрической прогрессии 12; -4; ; …

Вместе с учителем разбирается текст программы и учащиеся проверяют ее работу на компьютерах. Ответ сравнивается с тем, который получили при решении с помощью формулы.

Учитель.

У этой прогрессии , значит условие  выполняется. Разберем текст программы для вычисления суммы прогрессии без формулы для заданного  с помощью ЦИКЛА-ДО.

Текст программы

INPUT "e="; e

bn = 12

s = 0

DO WHILE ABS(bn) >= e

   s = s + bn

   bn = bn * (-1 / 3)

LOOP

PRINT "s=";

PRINT USING "###.#####"; s

END

Учитель.

Запустите программу и введите е=0,5. Запустите снова и введите е=0,1, потом е=0,01, е=0,0001.

К какому число приближается значение переменной s?

Верно ли составлена программа?

VI. Подведение итогов урока.

Учитель.

·        Что мы повторили на этом уроке?

·        Понятно ли вам, что означают в математике ряды?

·        Теперь вы представляете себе сходимые и расходимые последовательности?

·        Можно ли не зная формулы суммы бесконечной геометрической прогрессии найти ее?

·        С помощью чего можно это сделать?

·        Можно ли с помощью компьютера решать другие задачи на арифметическую и геометрическую прогрессию?

VII. Задание на дом.

Задания из учебника №433 (а), №446 (а), №480 (а).

Учитель объяснят, что решения данных заданий аналогичны тем, что выполнялись ими ранее.

VIII. Решение задач на сообразительность.

Если останется время, то можно предложить следующие задания. Задачи выводятся на экран телевизора, а текст читается учителем.

№1

В каждом числовом ряду числа следуют в определенной закономерности. Установите эту закономерность и запишите еще по два числа.

1.     19, 20, 22, 25, 29, …

2.     5, 8, 14, 26, 50, …

3.     253, 238, 223, 208, 193, …

4.     12, 11, 16, 16, 20, 21, 24, 26, …

5.     15, 29, 56, 109, 214, …

№2

Установите правило, по которому составлена таблица, и впишите недостающие числа: