Поделиться
Тестирование по алгебре с помощью нейросетей тема Функции Часть 2 9 класс.pdf
Тест по Алгебре проходит нейросеть.Часть2
Тест по Алгебре проходит нейросеть
Тест по Алгебре проходит нейросеть. Выполнение заданий
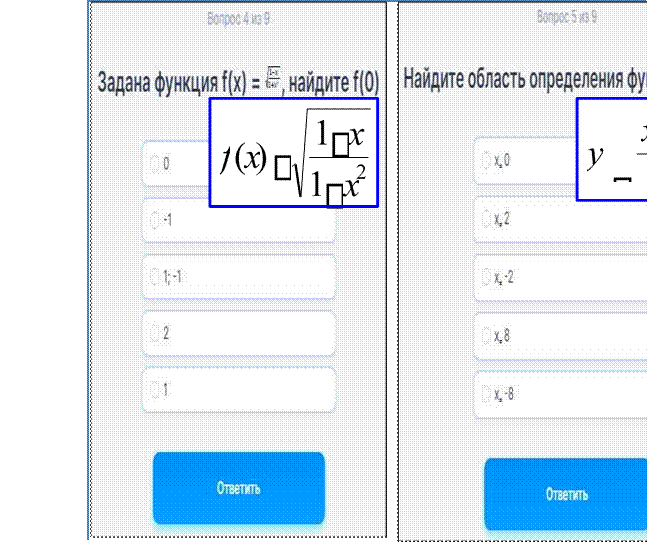
Задана функция f(x) =[(1-x)^1/2]/[(1+x^2)^1/2], найдите f(0)
Чтобы найти ( f(0) ) для функции ( f(x) = \frac{(1x)^{1/2}}{(1+x^2)^{1/2}} ), подставим ( x = 0 ):
[ f(0) = \frac{(1-0)^{1/2}}{(1+0^2)^{1/2}} = \frac{1^{1/2}}{1^{1/2}} = \frac{1}{1} = 1. ] Таким образом, ( f(0) = 1 ).
Задана функция y = (x^2+8)/(x+2), найдите ее область определения
Область определения функции ( y = \frac{x^2 + 8}{x + 2} ) — это множество всех значений ( x ), при которых функция корректно определена. В данном случае необходимо проверить, при каких значениях ( x ) знаменатель не равен нулю, так как деление на ноль не определено.
Знаменатель равен нулю, когда: [ x + 2 = 0 ] Отсюда: [ x = -2 ] Таким образом, функция не определена при ( x = -2 ). Все остальные значения ( x ) допустимы.
Записывая область определения в интервале, получаем: [ D =
\mathbb{R} \setminus {-2} ] или, в других обозначениях: [ D = (-\infty, -2) \cup (-2, +\infty) ]
Тест по Алгебре проходит нейросеть. Выполнение заданий
Найдите точки пересечения графика функции с осью абсцисс у = 3х - х^2
|
Чтобы найти точки пересечения графика функции \( y = 3x - x^2 \) с осью абсцисс, нужно решить уравнение, при котором \( y = 0 \). Уравнение выглядит так: \[3x - x^2 = 0\] Перепишем его: \[-x^2 + 3x = 0\] Вынесем общий множитель \( x \):\[x(3 - x) = 0\] Теперь у нас есть два множителя, равных нулю: 1. \( x = 0 \) 2. \( 3 - x = 0 \) \(\Rightarrow x = 3\) Следовательно, точки пересечения графика функции с осью абсцисс - это \( x = 0 \) и \( x = 3 \). Для нахождения координат этих точек пересечения подставим найденные значения \( x \): - Для \( x = 0 \): \( y = 3(0) - (0)^2 = 0 \) \(\Rightarrow (0, 0)\) -Для \( x = 3 \): \( y = 3(3) - (3)^2 = 9 - 9 = 0 \) \(\Rightarrow (3, 0)\) -Таким образом, точки пересечения графика функции с осью абсцисс: \((0, 0)\) и \((3, 0)\). |
Тест по Алгебре проходит нейросеть.Часть2
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
