Добавить материал

и получить 10 документов
и свидетельство СМИ

Изображение пользователя Сарафанова Ольга Владимировна Сарафанова Ольга Владимировна

Конспект урока "Формулы приведения"

  • Разработки уроков
  • doc
  • 27.12.2021
Публикация в СМИ для учителей

Публикация в СМИ для учителей

Бесплатное участие. Свидетельство СМИ сразу.
Мгновенные 10 документов в портфолио.

Добавить материал
Описание применения формул приведения с примерами, сопровожденными пояснениями
Иконка файла материала Формулы приведения.doc

Тема Формулы приведения

Формулами приведения называются соотношения с помощью которых значения тригонометрических функций аргументов  выражаются через значения .

Все формулы приведения можно свести в таблицу

 

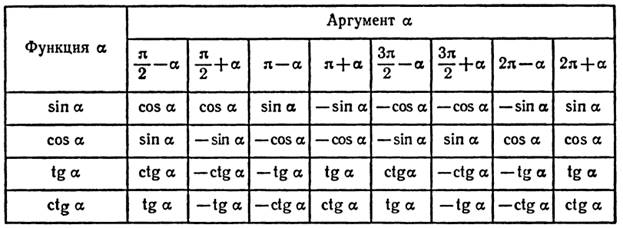
Для облегчения запоминания приведенных формул можно воспользоваться следующими правилами:

1)    Считая угол  острым углом (т.е. ) перед функцией поставить такой знак, который имеет приводимая функция (знак определяем по тому, в какую четверть попадает угол, знаки функций по четвертям смотри в теме «Синус и косинус. Тангенс и котангенс»).

2)    При переходе от функции углов  к функциям угла  название функции изменяют: синус на косинус, тангенс на котангенс и наоборот;

при переходе от функции углов  к функциям угла  название функции не изменяют.

 

Примеры применения формул приведения

1) Привести к тригонометрической функции острого угла и вычислить:

а) Sin 19350; б) Cos (-15600); в) tg(-23,25)

а) Решение

Решение

Пояснения

Т.к. через 3600 значения всех тригонометрических функций повторяются, то и через () тоже повторятся.

 

 - это угол II четверти, а функция синус больше нуля в этой четверти и 900 функцию меняет, т.е. синус на косинус.

 

Находим на тригонометрическом круге точку 450 и проецируем ее на ось OX (идем по пунктирной линии вниз до оси OX), находим значение

б) Решение

Решение

Пояснения

 

Т.к. функция косинус четная, то , а значит,

 

Т.к. через 3600 значения всех тригонометрических функций повторяются, то и через () тоже повторятся.

 

 - это угол II четверти, а функция косинус меньше нуля в этой четверти и 900 функцию меняет, т.е. косинус на синус.

 

Находим на тригонометрическом круге точку 300 и проецируем ее на ось OY (идем по пунктирной линии вправо до оси OY), находим значение , не забывая о минусе перед функцией

 

в) Решение

Решение

Пояснения

Т.к. функция тангенс нечетная, то , а значит,

 

Т.к. через  значения всех тригонометрических функций повторяются, то и через  тоже повторятся.

 

 - это угол II четверти, а функция тангенс меньше нуля, и  функцию не меняет.

 

Т к.  , то

 

находим по тригонометрическому кругу значения  и  и вычисляем их отношение.

2) Упростить выражение

2) Решение

Решение

Пояснения

Чтобы воспользоваться формулой приведения, вынесем минус за скобочку.

 

Т.к. функция косинус четная, то , а значит, .

 

 угол в I четверти, а косинус в первой четверти положителен и  функцию меняет (т.е. косинус на синус)

Чтобы воспользоваться формулой приведения, вынесем минус за скобочку.

 

Т.к. функция синус нечетная, то , а значит, .

 

 - угол II четверти, а синус положительный в этой четверти и  функцию не меняет.

 

 - это угол II четверти, а тангенс отрицательный в этой четверти и  функцию не меняет.

Чтобы воспользоваться формулой приведения, вынесем минус за скобочку.

 

Т.к. функция котангенс нечетная, то , а значит

 

 - это угол II четверти, котангенс в этой четверти отрицательный и  функцию не меняет.

Подставим все найденные значения в условие т.о.

=

=

 

Тема Формулы приведения Формулами приведения называются соотношения с помощью которых значения тригонометрических функций аргументов выражаются через значения Примеры применения формул приведения 1) Решение Решение Пояснения Чтобы воспользоваться формулой приведения, вынесем минус за скобочку

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

Посмотрите также