Конспект урока по алгебре и началам математического анализа по теме «Правила дифференцирования»

Урок № 52 (алгебра и начала мат. анализа)

Класс: 11

Учитель: Мосягина Ольга Эдуардовна

Тема урока: «Правила дифференцирования §46»

Цель урока: формирование умения находить производные суммы, произведения и частного.

Задачи урока:

1. Воспитательные: воспитание навыков самоконтроля и взаимоконтроля; воспитание культуры общения, умения работать в коллективе, взаимопомощи, умения организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками; воспитание качеств характера таких как, настойчивость в достижении цели, умение не растеряться в проблемных ситуациях; воспитание умения оценивать правильность выполнения учебной задачи, собственные возможности её решения; умения анализировать свою деятельность, делать самостоятельные выводы. 

2. Развивающие: развитие логического мышления; развитие умений в применении знаний в конкретной ситуации; развитие навыков реализации теоретических навыков в практической деятельности; развитие коммуникативной компетентности в общении и сотрудничестве; развитие внимания, мышления, памяти, самостоятельности; расширение кругозора.

3. Образовательные: изучение правил дифференцирования; показать применение правил дифференцирования при решении задач.

Тип урока: комбинированный урок.

Методы: показательно-иллюстративные с применением мультимедийных технологий: словесный, практический, контролирующий.

Формы работы: фронтальная, индивидуальная, групповая, самостоятельная работа.

Оборудование урока: компьютер, приложение Skype, презентация Microsoft Office PowerPoint, учебники.

Ход урока

1. Организационный момент.

Проверка подготовленности учащихся к занятию.

Приветствие учителя и учащихся.

2. Мотивация учебной деятельности учащихся, постановка темы, целей и задач урока, проверка домашнего задания.

На предыдущем уроке вы изучали понятие производной, научились находить производные некоторых функций. На сегодняшнем уроке мы продолжим изучение этой темы, в частности, научимся применять правила дифференцирования.

Повторим изученный теоретический материал.

3. Актуализация мыслительных процессов через организацию сопутствующего повторения.

Фронтальная работа с классом: отвечает один из учащихся, остальные при необходимости дополняют, исправляют ответ своего товарища.

Сформулируйте определение производной функции f(x).

Назовите формулы нахождения производной, которые вы изучили на прошлом уроке.

С’=0

(kx+b)’=k

(x²)’=2x

(x³)’=3x²

(xⁿ)’=nx^n-1

4. Изучение нового материала.

Словесное объяснение нового материала и работа с учебником §46 стр.240-242.

Учитель: Производная суммы равна сумме производных:

(демонстрация экрана и запись в тетрадях)

(f(x)+g(x))’=f’(x)+g’(x)

Рассмотрим пример 1. Найти производную функции f(x)=x²+x.

(демонстрация экрана и запись в тетрадях)

Пример 1. f(x)=x²+x;

f’(x)=(x²+x)’=(x²)’+(x)’=2x+1

Пример 2. Найти производную функции f(x)=2x³-5x²+3x+8.

f’(x)= (2x³-5x²+3x+8)’=(2x³)’- (5x²)’+(3x)’+8’= 6x²-10x+3.

Учитель: Рассмотрим второе правило дифференцирования.

Постоянный множитель можно вынести за знак производной:

 (cf(x))’=cf’(x)

Найти производную функции f(x)=8x³+3x²-x.

(демонстрация экрана и запись в тетрадях)

 f(x)=8x³+3x²-x;

f’(x)=(8x³)’+(3x²)’-x’;

Рассмотрим каждый член многочлена по отдельности.

(демонстрация экрана и запись в тетрадях)

(8x³)’=8(x³)’=8*3x²=24x²;

(3x²)’=3(x²)’=3*2x=6x;

(-x)’=-(x) = -1;

f’(x)=(8x³)’+(3x²)’-x’=24x²+6x-1.

Учитель: Переходим к третьему правилу дифференцирования. Запишем формулу, по которой находится производная произведения.

(демонстрация экрана и запись в тетрадях)

(f(x)*g(x))’=f’(x)*g(x)+f(x)*g’(x).

Учитель: Производная произведения равна произведению первого множителя на второй плюс первый множитель, умноженный на производную второго.

Рассмотрим задачу 3. Найти производную функции f(x)=(x²+x-6)(x²-x-2).

Воспользуемся формулой производной произведения.

(демонстрация экрана и запись в тетрадях)

 f(x)=(x²+x-6)(x²-x-2);

f’(x)=(x²+x-6)’(x²-x-2) + (x²+x-6)(x²-x-2)’= (2x+1) (x²-x-2)+ (x²+x-6)(2x-1)

Учитель: Можно оставить в виде произведения как в учебнике, а можно раскрыть скобки и получить многочлен третьей степени.

Переходим к следующей формуле.

(демонстрация экрана и запись в тетрадях)

)’= .

Учитель: производная частного равна производной числителя, умноженного на знаменатель минус числитель, умноженный на производную знаменателя и все это деленное на квадрат знаменателя.

Рассмотрим задачу 4. Найти производную функции

 f(x) =

(демонстрация экрана и запись в тетрадях)

f(x) = ;

f’(x) = ( )’=  =  =  = .

5. Здороровьесберегающие технологии.

Комплекс упражнений для снятия усталости глаз, профилактики близорукости и улучшения зрения –1 минута.

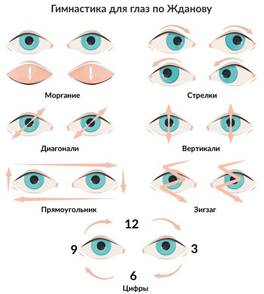
6. Первичное применение полученных знаний на практике. 

Демонстрация решения примеров.

Учитель: Применим эти правила при решении задач.

Пример1: Найти производную функции x²+x.

Учитель: Как связаны между собой функции x² и x? Какое правило дифференцирования надо использовать?

Ученик: Знаком плюс. Значит, надо применить правило производной суммы.

(демонстрация экрана и запись в тетрадях)

Задание №1.

(x²+x)’= 2x+1.

Пример2: Найти производную функции 8x².

Учитель: Объясните, по какому правилу будем находить производную этой функции?

Ученик: Числовой множитель можно вынести из под знака производной.

(демонстрация экрана и запись в тетрадях)

(8x²)’= 2*8x=16x.

Пример3: Найти производную функции -4x³.

(демонстрация экрана и запись в тетрадях)

 (-4x³)’=3*(-4x²) = -12x².

Ученик: Найти производную функции 13x²+26.

Учитель: Как найти производную этой функции?

Ученик: Воспользуемся правилом нахождения производной от суммы и вынесением числового множителя из под знака производной.

(демонстрация экрана и запись в тетрадях)

(13x²+26)’=26x.

7. Формирование умений и навыков решения упражнений применение основного свойства дроби.

1. Практическое решение заданий.

Учитель: Следующий №806.

(один ученик комментирует, остальные решают в тетради)

Ученик: Продифференцировать функцию 3x²-6x+6.

Учитель: Производную от трехчлена находят также, как и производную от двучлена.

(демонстрация экрана и запись в тетрадях)

 (3x²-6x+6)’= (3x²)’-(6x)’+6’=6x-6.

Ученик: Продифференцировать функцию x+12x².

Учитель: Какое правило дифференцирования применим?

Ученик: Правило нахождения производной суммы.

(демонстрация экрана и запись в тетрадях)

(x+12x²)’= 1+24x.

Ученик: Продифференцировать функцию x³+6x.

Ученик: Используем правила нахождения производной от суммы и вынесение числового множителя из-под знака производной.

(демонстрация экрана и запись в тетрадях)

 (x³+6x)’= 3x²+6.

Ученик: Продифференцировать функцию 2x³-8x²+6x+1.

(запись на доске и в тетрадях)

(2x³-8x²+6x+1)’=6x²-16x+6.

Учитель: Следующий №805.

(один ученик выходит к доске, остальные решают в тетради)

Ученик: Найти f’(0) и f’(2), если f(x)= x²-2x+1.

Ученик: Сначала находим производную функции, затем подставляем в нее значение х=0 и х=2.

(демонстрация экрана и запись в тетрадях)

№807.

f(x)= x²-2x+1.

           f’(x)=2x-2;

           f’(0)=-2;

           f’(2)=4-2=2

Ученик: если f(x) = -x³+2x².

(демонстрация экрана и запись в тетрадях)

3)f(x) = -x³+2x².

f’(x) = -3x²+4x;

f’(0) = 0;

f’(2) = -12+8= -4.

Учитель: Следующий №808.

(один ученик комментирует, остальные решают в тетради)

Ученик: Найти значения х, при которых значение производной функции f(x) равно 0(решить уравнение f’(x)=0), если f(x)=x³-2x.

Ученик: Сначала находим производную функции f(x)=x³-2x.

(демонстрация экрана и запись в тетрадях)

№808.

f(x)=x³-2x.

     f’(x)=3x²-2;

Ученик: Затем полученный результат приравниваем к нулю и находим х.

(демонстрация экрана и запись в тетрадях)

     3x²-2=0;

     3x²=2;

     x² = ;

     x₁ = n ; x₂ = - n .

Ученик: если f(x) = 2x³+3x²-12x-3.

(демонстрация экрана и запись в тетрадях)

3)f(x) = 2x³+3x²-12x-3.

    f’(x) = 6x²+6x-12;

    6x²+6x-12=0 / :6

    x²+x-2=0;

         x_1,2  =  = ;

         x₁ =1, x₂= -2.

Ученик: если f(x) = (x-2)²(x+1).

(демонстрация экрана и запись в тетрадях)

5)f(x) = (x-2)²(x+1).

f’(x) = 2(x-2)(x+1)+(x-2)²=(x-2)(2x+2+x-2) = (x-2)3x;

(x-2)3x=0;

x-2=0          3x=0

x=2              x=0

2. Самостоятельная работа. Решить самостоятельно (по группам, дифференцированные задания).

1 группа № 809 1); 2 группа № 809 2); 3 группа № 809 3).

Ответы демонстрируются на экран. Выполняется самопроверка.

8. Закрепление изученного материала.

Просмотр видео:

https://www.youtube.com/watch?v=zQ31lRoA6lQ

9. Подведение итогов урока. Информирование учащихся о домашнем задании и инструктаж по его выполнению.

Учить §46 стр.240-242.

Решить №803 (1; 2; 3); №806 письменно.

Желаю успехов!

10. Рефлексия.

Учитель задает вопросы, побуждая обучающихся к анализу своей деятельности на уроке. Выражает удовлетворение от работы на уроке, оценивает работу, благодарит за работу на уроке.

Скачано с www.znanio.ru