
КОНСПЕКТ УРОКА ПО ТЕМЕ
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
Цели:
· Обобщить и систематизировать материал по теме «ФСУ»; закрепить умения и навыки обучающихся в применении формул при решении различных заданий.
· Способствовать развитию обобщения как метода научного познания, развитие элементов творческой деятельности, умения контролировать свои действия, способностей к самооценке, развивать логическое мышление.
· Воспитывать интерес к данной теме, умение оценивать друг друга и давать себе самооценку; усидчивость, сознательность, активность, культуру учебного труда.
Задачи урока:
Образовательная: проверить уровень усвоения учащимися темы, знание ими соответствующих правил и формул.
Развивающая: уметь применять формулы сокращенного умножения на практике, развивать вычислительные навыки, логическое мышление, формировать навыки рационального счета, самоконтроля и взаимоконтроля, самоанализа своей учебной деятельности и развивать познавательный интерес учащихся, формирование метапредметных умений
Воспитательная: создание условий для включения каждого ученика в активную учебно-познавательную деятельность, где каждый может проявить себя, воспитание познавательного интереса к предмету, воспитывать собранность, внимательность.
Тип урока: комбинированный.
Методы: словесный, объяснительно-иллюстративный.
Формы организации познавательной деятельности: индивидуальная, коллективная, в парах.
Оборудование:
· учебник, доска, ученическая тетрадь;
· карточки с индивидуальными заданиями;
· оценочные листы
· тесты
План урока.
1. Организационный момент
2. Вводная беседа. Актуализация знаний
3. Планирование
4. Проверка домашнего задания
5. Практическая деятельность учащихся
6. Физкультминутка
7. Осуществление контроля
8. Осуществление коррекции
9. Итог урока
10. Оценивание учащихся
11. Рефлексия
12. Домашнее задание
На доске эпиграф:
«Единственный путь, ведущий к знаниям – это
деятельность»
Бернард Шоу.
Ход урока
1. Организационный момент
На столах у учащихся карточки с индивидуальным заданием, оценочные листы
Я рада приветствовать всех Вас на сегодняшнем уроке. Все мы с вами пришли на урок с разным настроением. Перед Вами лежат листы на которых нарисованы три лица, выражающих разное настроение. Выберете то, которое подходит к Вашему настроению. В конце урока мы также оценим свое настроение, надеюсь оно будет у вас хорошим.
2. Вводная беседа. Актуализация знаний
«У математиков существует свой язык – это формулы» и как вы думаете, чему будет посвящен наш сегодняшний урок?
Правильно наш сегодняшний урок посвящен формулам сокращенного умножения.
Для чего нужно знать формулы сокращенного умножения? (ответы учащихся)
Формулы сокращенного умножения имеют широкое применение в математике, особенно в старших классах.
Где их используют? при решении уравнений, раскрытии скобок, разложении многочленов на множители, нахождении значений выражений.
Видите сколько функций позволяют выполнять формулы сокращенного умножения, поэтому знать их нужно очень хорошо.
Прежде, чем приступить к работе, каждый из вас должен поставить перед собой цель сегодняшнего урока. Перед вами лежат оценочные листы, в левом столбце написаны цели, выберите те, которые соответствуют вашим, и отметьте их в кружочек или допишите свою. На каждом этапе урока вы будете оценивать себя или своих товарищей, выставляя количество заработанных баллов в оценочные листы.
Оценочный лист
Фамилия и имя ученика ______________________ Число___________
Тема урока _______________________________________________________________
|
№ |
Цели: |
№ |
Этапы урока |
Баллы |
|
|
1. |
Показать свои знания. |
1. |
Знание формул ФСУ |
|
из 4 |
|
2. |
Получить новые знания |
2. |
Провести соответствия |
|
из 8 |
|
3 |
Получить хорошую оценку |
3. |
Найти ошибку |
|
из 5 |
|
4. |
|
4. |
Тест |
|
из 4 |
|
5. |
|
5. |
Тест (устранение ошибок) |
|
из 5 |
Итог: _________ из 26___
Оценка: __________
|
Достиг ли ты своих целей? _________________________ Оцени степень усвоения: ____________________________ плохо, средне, хорошо, очень хорошо |
|
Продолжи одно из предложений: ______________ “Мне понятно… “Я запомнил… “Мне на уроке…
|
3. Планирование
Итак как вы думаете, как мы будем работать на уроке?На уроке мы обобщим знания, полученные ранее по темам квадрат суммы и разности, разность квадратов
В конце урока каждый из вас сможет оценить самостоятельно свои знания и умения.
 4.
Проверка домашнего задания
4.
Проверка домашнего задания
(1/4х2+4а)2
№845,846а
 |
(х2-4у2)2
Практическая деятельность учащихся
(16a3+b4)2
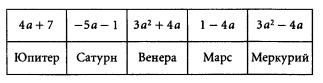
Игра «Закончи предложение»
Итак, какой ответ получился под буквой а) б) в) г) а)

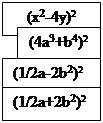
№875
64р2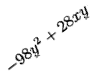
![]()
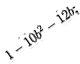
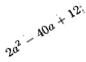
![]()
![]()
![]()
![]()
![]()

Венера
![]()
г в б а
№893а-д
![]()
 |
|||
|
|||
5. Практическая деятельность учащихся
Учащимся раздается комплект разрезанных предложений, задача найти нужные концовки предложений и подобрать формулы
|
1. Квадрат суммы двух выражений равен |
квадрату первого выражения плюс удвоенное произведение первого и второго выражения плюс квадрат второго выражения |
(I + II)2=I2 + 2·I·II + II2 |
|
2 Произведение разности двух выражений и их суммы равно |
произведению разности этих выражений и их суммы |
(I - II)2=I2 - 2·I·II + II2 |
|
3. Квадрат первого выражения минус удвоенное произведение первого и второго выражения плюс квадрат второго выражения равен |
разности квадратов этих выражений |
I2 - 2·I·II + II2 =(I - II)2 |
|
4. Разность квадратов двух выражений равна |
квадрату разности двух выражений |
(I - II) (I + II)=I2 - II2 |
Проведите соответствия
|
А) (k – y)2 |
|
1) k4 – 10k2y
+ 25y2 |
И |
|
А |
|
|
К |
|
Б |
|
|||
|
Е |
|
В |
|
|||
|
А |
|
Г |
|
|||
|
М |
|
Д |
|
|||
|
О |
|
Е |
|
|||
|
Т |
|
|
И |
|||
|
С |
|
Ж |
|
|||
|
|
|
З |
|
Ответы: А8, Б3, В5, Г1, Д6, Е7, Ж2, З4.
Учащиеся меняются тетрадями и проверяют задания друг у друга, сравнивая с ответами на доске.
СЕМИОТИКА

Работа в тетрадях с проверкой у доски.
Ученику нужно найти ошибку в каждой формуле и исправить ее на своих листах.
1) (4у – 3х)(4у+3х) = 8у2
– 9у2 (вместо 8у2 должно быть16у2).
2) 100х2 – 4у2 = (50х – 2у)(50х + 2у) (вместо 50х должно
быть10х).
3) (3х + у)2= 9х2 – 6ху + у2 (вместо -6ху
должно быть +6ху).
4) (6a – 9c)2 = 36a2 – 54ac + 81c2 (вместо
-54ac должно быть -108ac).
Затем вызываю учеников к доске исправить ошибки в примерах, они еще раз
проговаривают формулы и правила.
6. Физкультминутка
Эмоциональная разрядка:
· нахмуриться, как осенняя туча, рассерженный человек, злая волшебница
· улыбнуться, как кот на солнце, Буратино, хитрая лиса, ребенок, который увидел чудо
· устать, как папа после работы, человек, поднявший груз, муравей, притащивший большую муху
· отдохнуть как турист, снявший тяжелый рюкзак, ребенок, который много потрудился, уставший воин.
7. Осуществление контроля
Тест
|
I вариант Раскройте скобки: 1. (x + 2) 2 2. (3a + b) 2 • А. x2+2x +4 А. 9a2+b2 • Б. x2+4x +4 Б. 9a2+6ab +b2 • В. x+4x +4 В. 9a2+3ab+b2 • Г. x2+4 Г. 3a2+6ab+b2 3. (2a - 3) 2 4. (7 - b) 2 • А. 4a2-6a+9 А. 49-b2 • Б. 4a2-12a+9 Б. 49+b2-7b • В. 2a2-12a+9 В. 49-14b +b2 • Г. 4a2-9 Г.49+b2 5. (4x - 3y)(4x+3y) 6. (x -7y)(7y +x) • А. 4x2-3y2 А. x2-7y2 • Б. 4x2-6y2 Б. x2-49y • В. 16x2-9y2 В. x2-49y2 • Г. 16x2+9y2 Г. x2+49y2 |
ΙI вариант Раскройте скобки: 1. (x - 3) 2 2. (2a + b) 2 • А. x2-3x +9 А. 4a2+b2 • Б. x-6x +9 Б. 4a2+2ab+b2 • В. x2-6x +9 В. 4a2+4ab +b2 • Г. x2-9 Г. 2a2+4ab+b2 3. (3a - 2) 2 4. (5+ b) 2 • А. 9a2-6a+4 А. 25-b2 • Б. 3a2-12a+4 Б. 25+10b +b2 • В. 9a2-12a+4 В. 25+b2+5b • Г. 9a2-4 Г. 25+b2 5. (2x - 6y)(2x+6y) 6. (x -9y)(9y +x) • А. 4x2-6y2 А. x2-9y2 • Б. 4x2-36y2 Б. x2-81y2 • В. 2x2-36y2 В. x2-81y • Г. 4x2+36y2 Г. x2+81y2 |
Разбор ответов
1 ВАРИАНТ
1 Б
2 Б
3 Б
4 В
5 В
6 В
2 ВАРИАНТ
1 Б
2 В
3 В
4 Б
5 Б
6 Б
8. Осуществление коррекции
Тест.
Вариант 1.
1. Раскройте скобки (х + 3у)2
а) х2 + 6ху + 3у2
б) х2 + 9у2
в) х2 + 6ху + 9у2
г) х2 + 3ху + 9у2
2. Раскройте скобки (4а - 1)2
а) 16а2 — 4а + 1
б) 16а2 — 8а + 1
в) 4а2 — 4а + 1
г) 16а2 -1
3. (4х - 3у2)(4х + 3у2)
а) 4х2 — 3у4
б) 16х2 — 9у4
в) 16х2 + 9у4
г) 4х2 — 9у2
4. Равенство верно или нет
(х + 4у)2 = х2 + 16у2 + 8ху
а) да
б) нет
Вариант 2.
1. Раскройте скобки (2а - 5)2
а) 2а2 - 20а + 25
б) 4а2 - 10а + 25
в) 4а2 - 20а + 25
г) 4а2 + 20а + 25
2. Раскройте скобки (х + 5у)2
а) х2 — 10ху + 25у2
б) х2 + 10ху + 5у2
в) х2 + 10х + 25у2
г) х2 + 10ху + 25у2
3. (5в + 8а)(5в - 8а)
а) (8а + 5в)2
б) 64а2 — 25в2
в) 25в2 - 64а2
г) 25в2 — 8а2
4. Равенство верно или нет
(х + 4у)2 = х2 + 16у2 + 8ху
а) да
б) нет
ВАРИАНТ 1
1 В 2 Б 3Б 4Б
ВАРИАНТ 2
1 В 2 В 3Б 4В
9. Подведение итогов урока.
А теперь побеседуем. Чем мы сегодня занимались на уроке? Сегодня на уроке мы с вами... (ответы учащихся: обобщали и систематизировали материал по теме «ФСУ»; закрепляли умения и навыки в применении формул при решении различных заданий).
Нужны ли нам все изученные понятия в жизни? Как они нам помогают?
- Что удалось на уроке и над чем необходимо поработать?
- Достигли ли вы поставленной цели? Отметьте на листе и степень усвоения
10. Оценивание учащихся
Отметьте количество полученных баллов на листе. Всего 26 баллов
13-18 «3», 19-23 «4», 24-26 «5»
11.Рефлексия
Я, в свою очередь хочу сказать спасибо вам, ребята, за вашу активную работу на сегодняшнем уроке, думаю, что вы легко сможете применять все изученное в жизни. А теперь карандашом закрасите тот смайлик, который соответствует вашему настроению на конец урока.
12. Домашнее задание
На отдельных листах, подготовка к контрольной работе
• «3»- 3 номера
• «4»-4 номера
• «5»-5 номеров
1.Преобразуйте в многочлен:
а) (c + 7)2; в) (3x – 4)(3x + 4);
б) (5c – 2)2; г) (a 2 + 2)(a 2 – 2).
2.Разложите на множители:
а) – b 2; б) y 2 + 12y + 36.
3.Найдите значение выражения (3x – y)2 – 3x(3x – 2y) при y = – .
4. Выполните действия:
а) 5(3mn + 1)(3mn – 1); в) (c – d)2 – (c + d)2.
б) (a 3 – b 4) 2;
5.Решите уравнение:
а) (5х – 1)(5х + 1) – (5x + 2)2 = 0; б) 36b2 – 121 = 0.
Оценочный лист
Фамилия и имя ученика ______________________ Число___________
Тема урока _______________________________________________________________
|
№ |
Цели: |
№ |
Этапы урока |
Баллы |
|
|
1. |
Показать свои знания. |
1. |
Знание формул ФСУ |
|
из 4 |
|
2. |
Получить новые знания |
2. |
Провести соответствия |
|
из 8 |
|
3 |
Получить хорошую оценку |
3. |
Найти ошибку |
|
из 5 |
|
4. |
|
4. |
Тест |
|
из 4 |
|
5. |
|
5. |
Тест (устранение ошибок) |
|
из 5 |
Итог: _________ из 26___
Оценка: __________
|
Достиг ли ты своих целей? _________________________ Оцени степень усвоения: ____________________________ плохо, средне, хорошо, очень хорошо |
|
Продолжи одно из предложений: ______________ “Мне понятно… “Я запомнил… “Мне на уроке…
|
Оценочный лист
Фамилия и имя ученика ______________________ Число___________
Тема урока _______________________________________________________________
|
№ |
Цели: |
№ |
Этапы урока |
Баллы |
|
|
1. |
Показать свои знания. |
1. |
Знание формул ФСУ |
|
из 4 |
|
2. |
Получить новые знания |
2. |
Провести соответствия |
|
из 8 |
|
3 |
Получить хорошую оценку |
3. |
Найти ошибку |
|
из 5 |
|
4. |
|
4. |
Тест |
|
из 4 |
|
5. |
|
5. |
Тест (устранение ошибок) |
|
из 5 |
Итог: _________ из 26___
Оценка: __________
|
Достиг ли ты своих целей? _________________________ Оцени степень усвоения: ____________________________ плохо, средне, хорошо, очень хорошо |
|
Продолжи одно из предложений: ______________ “Мне понятно… “Я запомнил… “Мне на уроке…
|
Оценочный лист
Фамилия и имя ученика ______________________ Число___________
Тема урока _______________________________________________________________
|
№ |
Цели: |
№ |
Этапы урока |
Баллы |
|
|
1. |
Показать свои знания. |
1. |
Знание формул ФСУ |
|
из 4 |
|
2. |
Получить новые знания |
2. |
Провести соответствия |
|
из 8 |
|
3 |
Получить хорошую оценку |
3. |
Найти ошибку |
|
из 5 |
|
4. |
|
4. |
Тест |
|
из 4 |
|
5. |
|
5. |
Тест (устранение ошибок) |
|
из 5 |
Итог: _________ из 26___
Оценка: __________
|
Достиг ли ты своих целей? _________________________ Оцени степень усвоения: ____________________________ плохо, средне, хорошо, очень хорошо |
|
Продолжи одно из предложений: ______________ “Мне понятно… “Я запомнил… “Мне на уроке…
|
|
1. Квадрат суммы двух выражений равен |
1. Квадрат суммы двух выражений равен |
|
2 Произведение разности двух выражений и их суммы равно |
2 Произведение разности двух выражений и их суммы равно |
|
3. Квадрат первого выражения минус удвоенное произведение первого и второго выражения плюс квадрат второго выражения равен |
3. Квадрат первого выражения минус удвоенное произведение первого и второго выражения плюс квадрат второго выражения равен |
|
4. Разность квадратов двух выражений равна |
4. Разность квадратов двух выражений равна |
|
1. Квадрат суммы двух выражений равен |
1. Квадрат суммы двух выражений равен |
|
2 Произведение разности двух выражений и их суммы равно |
2 Произведение разности двух выражений и их суммы равно |
|
3. Квадрат первого выражения минус удвоенное произведение первого и второго выражения плюс квадрат второго выражения равен |
3. Квадрат первого выражения минус удвоенное произведение первого и второго выражения плюс квадрат второго выражения равен |
|
4. Разность квадратов двух выражений равна |
4. Разность квадратов двух выражений равна |
|
1. Квадрат суммы двух выражений равен |
1. Квадрат суммы двух выражений равен |
|
2 Произведение разности двух выражений и их суммы равно |
2 Произведение разности двух выражений и их суммы равно |
|
3. Квадрат первого выражения минус удвоенное произведение первого и второго выражения плюс квадрат второго выражения равен |
3. Квадрат первого выражения минус удвоенное произведение первого и второго выражения плюс квадрат второго выражения равен |
|
4. Разность квадратов двух выражений равна |
4. Разность квадратов двух выражений равна |
|
1. Квадрат суммы двух выражений равен |
1. Квадрат суммы двух выражений равен |
|
2 Произведение разности двух выражений и их суммы равно |
2 Произведение разности двух выражений и их суммы равно |
|
3. Квадрат первого выражения минус удвоенное произведение первого и второго выражения плюс квадрат второго выражения равен |
3. Квадрат первого выражения минус удвоенное произведение первого и второго выражения плюс квадрат второго выражения равен |
|
4. Разность квадратов двух выражений равна |
4. Разность квадратов двух выражений равна |
|
1. Квадрат суммы двух выражений равен |
1. Квадрат суммы двух выражений равен |
|
2 Произведение разности двух выражений и их суммы равно |
2 Произведение разности двух выражений и их суммы равно |
|
3. Квадрат первого выражения минус удвоенное произведение первого и второго выражения плюс квадрат второго выражения равен |
3. Квадрат первого выражения минус удвоенное произведение первого и второго выражения плюс квадрат второго выражения равен |
|
4. Разность квадратов двух выражений равна |
4. Разность квадратов двух выражений равна |
|
квадрату первого выражения плюс удвоенное произведение первого и второго выражения плюс квадрат второго выражения |
(I + II)2=I2 + 2·I·II + II2 |
|
произведению разности этих выражений и их суммы |
(I - II)2=I2 - 2·I·II + II2 |
|
разности квадратов этих выражений |
I2 - 2·I·II + II2 =(I - II)2 |
|
квадрату разности двух выражений |
(I - II) (I - II)=I2 - II2 |
|
квадрату первого выражения плюс удвоенное произведение первого и второго выражения плюс квадрат второго выражения |
(I + II)2=I2 + 2·I·II + II2 |
|
произведению разности этих выражений и их суммы |
(I - II)2=I2 - 2·I·II + II2 |
|
разности квадратов этих выражений |
I2 - 2·I·II + II2 =(I - II)2 |
|
квадрату разности двух выражений |
(I - II) (I - II)=I2 - II2 |
|
квадрату первого выражения плюс удвоенное произведение первого и второго выражения плюс квадрат второго выражения |
(I + II)2=I2 + 2·I·II + II2 |
|
произведению разности этих выражений и их суммы |
(I - II)2=I2 - 2·I·II + II2 |
|
разности квадратов этих выражений |
I2 - 2·I·II + II2 =(I - II)2 |
|
квадрату разности двух выражений |
(I - II) (I - II)=I2 - II2 |
|
квадрату первого выражения плюс удвоенное произведение первого и второго выражения плюс квадрат второго выражения |
(I + II)2=I2 + 2·I·II + II2 |
|
произведению разности этих выражений и их суммы |
(I - II)2=I2 - 2·I·II + II2 |
|
разности квадратов этих выражений |
I2 - 2·I·II + II2 =(I - II)2 |
|
квадрату разности двух выражений |
(I - II) (I - II)=I2 - II2 |
|
квадрату первого выражения плюс удвоенное произведение первого и второго выражения плюс квадрат второго выражения |
(I + II)2=I2 + 2·I·II + II2 |
|
произведению разности этих выражений и их суммы |
(I - II)2=I2 - 2·I·II + II2 |
|
разности квадратов этих выражений |
I2 - 2·I·II + II2 =(I - II)2 |
|
квадрату разности двух выражений |
(I - II) (I - II)=I2 - II2 |
|
квадрату первого выражения плюс удвоенное произведение первого и второго выражения плюс квадрат второго выражения |
(I + II)2=I2 + 2·I·II + II2 |
|
произведению разности этих выражений и их суммы |
(I - II)2=I2 - 2·I·II + II2 |
|
разности квадратов этих выражений |
I2 - 2·I·II + II2 =(I - II)2 |
|
квадрату разности двух выражений |
(I - II) (I - II)=I2 - II2 |
|
квадрату первого выражения плюс удвоенное произведение первого и второго выражения плюс квадрат второго выражения |
(I + II)2=I2 + 2·I·II + II2 |
|
произведению разности этих выражений и их суммы |
(I - II)2=I2 - 2·I·II + II2 |
|
разности квадратов этих выражений |
I2 - 2·I·II + II2 =(I - II)2 |
|
квадрату разности двух выражений |
(I - II) (I - II)=I2 - II2 |
1 Проведите соответствия
|
А) (k – y)2 |
пппп |
1) k4 – 10k2y
+ 25y2 |
И |
ппп |
А |
|
|
К |
|
Б |
|
|||
|
Е |
|
В |
|
|||
|
А |
|
Г |
|
|||
|
М |
|
Д |
|
|||
|
О |
|
Е |
|
|||
|
Т |
|
|
И |
|||
|
С |
|
Ж |
|
|||
|
|
|
З |
|
СЛОВО__________________________
1 Проведите соответствия
|
А) (k – y)2 |
пппп |
1) k4 – 10k2y
+ 25y2 |
И |
ппп |
А |
|
|
К |
|
Б |
|
|||
|
Е |
|
В |
|
|||
|
А |
|
Г |
|
|||
|
М |
|
Д |
|
|||
|
О |
|
Е |
|
|||
|
Т |
|
|
И |
|||
|
С |
|
Ж |
|
|||
|
|
|
З |
|
СЛОВО__________________________
1 Проведите соответствия
|
А) (k – y)2 |
пппп |
1) k4 – 10k2y
+ 25y2 |
И |
ппп |
А |
|
|
К |
|
Б |
|
|||
|
Е |
|
В |
|
|||
|
А |
|
Г |
|
|||
|
М |
|
Д |
|
|||
|
О |
|
Е |
|
|||
|
Т |
|
|
И |
|||
|
С |
|
Ж |
|
|||
|
|
|
З |
|
СЛОВО__________________________
2Найти ошибку в каждой формуле и исправить
1) (4у – 3х)(4у+3х) = 8у2 – 9у2
2) 100х2 – 4у2 = (50х – 2у)(50х + 2у)
3) (3х + у)2= 9х2 – 6ху + у2
4) (6a – 9c)2 = 36a2 – 54ac + 81c2
2Найти ошибку в каждой формуле и исправить
1) (4у – 3х)(4у+3х) = 8у2 – 9у2
2) 100х2 – 4у2 = (50х – 2у)(50х + 2у)
3) (3х + у)2= 9х2 – 6ху + у2
4) (6a – 9c)2 = 36a2 – 54ac + 81c2
2Найти ошибку в каждой формуле и исправить
1) (4у – 3х)(4у+3х) = 8у2 – 9у2
2) 100х2 – 4у2 = (50х – 2у)(50х + 2у)
3) (3х + у)2= 9х2 – 6ху + у2
4) (6a – 9c)2 = 36a2 – 54ac + 81c2
2Найти ошибку в каждой формуле и исправить
1) (4у – 3х)(4у+3х) = 8у2 – 9у2
2) 100х2 – 4у2 = (50х – 2у)(50х + 2у)
3) (3х + у)2= 9х2 – 6ху + у2
4) (6a – 9c)2 = 36a2 – 54ac + 81c2
2Найти ошибку в каждой формуле и исправить
1) (4у – 3х)(4у+3х) = 8у2 – 9у2
2) 100х2 – 4у2 = (50х – 2у)(50х + 2у)
3) (3х + у)2= 9х2 – 6ху + у2
4) (6a – 9c)2 = 36a2 – 54ac + 81c2
2Найти ошибку в каждой формуле и исправить
1) (4у – 3х)(4у+3х) = 8у2 – 9у2
2) 100х2 – 4у2 = (50х – 2у)(50х + 2у)
3) (3х + у)2= 9х2 – 6ху + у2
4) (6a – 9c)2 = 36a2 – 54ac + 81c2
2Найти ошибку в каждой формуле и исправить
1) (4у – 3х)(4у+3х) = 8у2 – 9у2
2) 100х2 – 4у2 = (50х – 2у)(50х + 2у)
3) (3х + у)2= 9х2 – 6ху + у2
4) (6a – 9c)2 = 36a2 – 54ac + 81c2
2Найти ошибку в каждой формуле и исправить
1) (4у – 3х)(4у+3х) = 8у2 – 9у2
2) 100х2 – 4у2 = (50х – 2у)(50х + 2у)
3) (3х + у)2= 9х2 – 6ху + у2
4) (6a – 9c)2 = 36a2 – 54ac + 81c2
2Найти ошибку в каждой формуле и исправить
1) (4у – 3х)(4у+3х) = 8у2 – 9у2
2) 100х2 – 4у2 = (50х – 2у)(50х + 2у)
3) (3х + у)2= 9х2 – 6ху + у2
4) (6a – 9c)2 = 36a2 – 54ac + 81c2
2Найти ошибку в каждой формуле и исправить
1) (4у – 3х)(4у+3х) = 8у2 – 9у2
2) 100х2 – 4у2 = (50х – 2у)(50х + 2у)
3) (3х + у)2= 9х2 – 6ху + у2
4) (6a – 9c)2 = 36a2 – 54ac + 81c2
2Найти ошибку в каждой формуле и исправить
1) (4у – 3х)(4у+3х) = 8у2 – 9у2
2) 100х2 – 4у2 = (50х – 2у)(50х + 2у)
3) (3х + у)2= 9х2 – 6ху + у2
4) (6a – 9c)2 = 36a2 – 54ac + 81c2
2Найти ошибку в каждой формуле и исправить
1) (4у – 3х)(4у+3х) = 8у2 – 9у2
2) 100х2 – 4у2 = (50х – 2у)(50х + 2у)
3) (3х + у)2= 9х2 – 6ху + у2
4) (6a – 9c)2 = 36a2 – 54ac + 81c2
2Найти ошибку в каждой формуле и исправить
1) (4у – 3х)(4у+3х) = 8у2 – 9у2
2) 100х2 – 4у2 = (50х – 2у)(50х + 2у)
3) (3х + у)2= 9х2 – 6ху + у2
4) (6a – 9c)2 = 36a2 – 54ac + 81c2
2Найти ошибку в каждой формуле и исправить
1) (4у – 3х)(4у+3х) = 8у2 – 9у2
2) 100х2 – 4у2 = (50х – 2у)(50х + 2у)
3) (3х + у)2= 9х2 – 6ху + у2
4) (6a – 9c)2 = 36a2 – 54ac + 81c2
3 Тест
|
I вариант Раскройте скобки: 1. (x + 2) 2 2. (3a + b) 2 • А. x2+2x +4 А. 9a2+b2 • Б. x2+4x +4 Б. 9a2+6ab +b2 • В. x+4x +4 В. 9a2+3ab+b2 • Г. x2+4 Г. 3a2+6ab+b2 3. (2a - 3) 2 4. (7 - b) 2 • А. 4a2-6a+9 А. 49-b2 • Б. 4a2-12a+9 Б. 49+b2-7b • В. 2a2-12a+9 В. 49-14b +b2 • Г. 4a2-9 Г.49+b2 5. (4x - 3y)(4x+3y) 6. (x -7y)(7y +x) • А. 4x2-3y2 А. x2-7y2 • Б. 4x2-6y2 Б. x2-49y • В. 16x2-9y2 В. x2-49y2 • Г. 16x2+9y2 Г. x2+49y2 |
ΙI вариант Раскройте скобки: 1. (x - 3) 2 2. (2a + b) 2 • А. x2-3x +9 А. 4a2+b2 • Б. x-6x +9 Б. 4a2+2ab+b2 • В. x2-6x +9 В. 4a2+4ab +b2 • Г. x2-9 Г. 2a2+4ab+b2 3. (3a - 2) 2 4. (5+ b) 2 • А. 9a2-6a+4 А. 25-b2 • Б. 3a2-12a+4 Б. 25+10b +b2 • В. 9a2-12a+4 В. 25+b2+5b • Г. 9a2-4 Г. 25+b2 5. (2x - 6y)(2x+6y) 6. (x -9y)(9y +x) • А. 4x2-6y2 А. x2-9y2 • Б. 4x2-36y2 Б. x2-81y2 • В. 2x2-36y2 В. x2-81y • Г. 4x2+36y2 Г. x2+81y2 |
3 Тест
|
I вариант Раскройте скобки: 1. (x + 2) 2 2. (3a + b) 2 • А. x2+2x +4 А. 9a2+b2 • Б. x2+4x +4 Б. 9a2+6ab +b2 • В. x+4x +4 В. 9a2+3ab+b2 • Г. x2+4 Г. 3a2+6ab+b2 3. (2a - 3) 2 4. (7 - b) 2 • А. 4a2-6a+9 А. 49-b2 • Б. 4a2-12a+9 Б. 49+b2-7b • В. 2a2-12a+9 В. 49-14b +b2 • Г. 4a2-9 Г.49+b2 5. (4x - 3y)(4x+3y) 6. (x -7y)(7y +x) • А. 4x2-3y2 А. x2-7y2 • Б. 4x2-6y2 Б. x2-49y • В. 16x2-9y2 В. x2-49y2 • Г. 16x2+9y2 Г. x2+49y2 |
ΙI вариант Раскройте скобки: 1. (x - 3) 2 2. (2a + b) 2 • А. x2-3x +9 А. 4a2+b2 • Б. x-6x +9 Б. 4a2+2ab+b2 • В. x2-6x +9 В. 4a2+4ab +b2 • Г. x2-9 Г. 2a2+4ab+b2 3. (3a - 2) 2 4. (5+ b) 2 • А. 9a2-6a+4 А. 25-b2 • Б. 3a2-12a+4 Б. 25+10b +b2 • В. 9a2-12a+4 В. 25+b2+5b • Г. 9a2-4 Г. 25+b2 5. (2x - 6y)(2x+6y) 6. (x -9y)(9y +x) • А. 4x2-6y2 А. x2-9y2 • Б. 4x2-36y2 Б. x2-81y2 • В. 2x2-36y2 В. x2-81y • Г. 4x2+36y2 Г. x2+81y2 |
3 Тест
|
I вариант Раскройте скобки: 1. (x + 2) 2 2. (3a + b) 2 • А. x2+2x +4 А. 9a2+b2 • Б. x2+4x +4 Б. 9a2+6ab +b2 • В. x+4x +4 В. 9a2+3ab+b2 • Г. x2+4 Г. 3a2+6ab+b2 3. (2a - 3) 2 4. (7 - b) 2 • А. 4a2-6a+9 А. 49-b2 • Б. 4a2-12a+9 Б. 49+b2-7b • В. 2a2-12a+9 В. 49-14b +b2 • Г. 4a2-9 Г.49+b2 5. (4x - 3y)(4x+3y) 6. (x -7y)(7y +x) • А. 4x2-3y2 А. x2-7y2 • Б. 4x2-6y2 Б. x2-49y • В. 16x2-9y2 В. x2-49y2 • Г. 16x2+9y2 Г. x2+49y2 |
ΙI вариант Раскройте скобки: 1. (x - 3) 2 2. (2a + b) 2 • А. x2-3x +9 А. 4a2+b2 • Б. x-6x +9 Б. 4a2+2ab+b2 • В. x2-6x +9 В. 4a2+4ab +b2 • Г. x2-9 Г. 2a2+4ab+b2 3. (3a - 2) 2 4. (5+ b) 2 • А. 9a2-6a+4 А. 25-b2 • Б. 3a2-12a+4 Б. 25+10b +b2 • В. 9a2-12a+4 В. 25+b2+5b • Г. 9a2-4 Г. 25+b2 5. (2x - 6y)(2x+6y) 6. (x -9y)(9y +x) • А. 4x2-6y2 А. x2-9y2 • Б. 4x2-36y2 Б. x2-81y2 • В. 2x2-36y2 В. x2-81y • Г. 4x2+36y2 Г. x2+81y2 |
4 Тест на исправление ошибок
Вариант 1.
1. Раскройте скобки (х + 3у)2
а) х2 + 6ху + 3у2
б) х2 + 9у2
в) х2 + 6ху + 9у2
г) х2 + 3ху + 9у2
2. Раскройте скобки (4а - 1)2
а) 16а2 — 4а + 1
б) 16а2 — 8а + 1
в) 4а2 — 4а + 1
г) 16а2 -1
3. (4х - 3у2)(4х + 3у2)
а) 4х2 — 3у4
б) 16х2 — 9у4
в) 16х2 + 9у4
г) 4х2 — 9у2
4. Равенство верно или нет
(х + 4у)2 = х2 + 16у2 + 8ху
а) да
б) нет
Вариант 2.
1. Раскройте скобки (2а - 5)2
а) 2а2 - 20а + 25
б) 4а2 - 10а + 25
в) 4а2 - 20а + 25
г) 4а2 + 20а + 25
2. Раскройте скобки (х + 5у)2
а) х2 — 10ху + 25у2
б) х2 + 10ху + 5у2
в) х2 + 10х + 25у2
г) х2 + 10ху + 25у2
3. (5в + 8а)(5в - 8а)
а) (8а + 5в)2
б) 64а2 — 25в2
в) 25в2 - 64а2
г) 25в2 — 8а2
4. Равенство верно или нет
(х + 4у)2 = х2 + 16у2 + 8ху
а) да
б) нет
4 Тест на исправление ошибок
Вариант 1.
1. Раскройте скобки (х + 3у)2
а) х2 + 6ху + 3у2
б) х2 + 9у2
в) х2 + 6ху + 9у2
г) х2 + 3ху + 9у2
2. Раскройте скобки (4а - 1)2
а) 16а2 — 4а + 1
б) 16а2 — 8а + 1
в) 4а2 — 4а + 1
г) 16а2 -1
3. (4х - 3у2)(4х + 3у2)
а) 4х2 — 3у4
б) 16х2 — 9у4
в) 16х2 + 9у4
г) 4х2 — 9у2
4. Равенство верно или нет
(х + 4у)2 = х2 + 16у2 + 8ху
а) да
б) нет
Вариант 2.
1. Раскройте скобки (2а - 5)2
а) 2а2 - 20а + 25
б) 4а2 - 10а + 25
в) 4а2 - 20а + 25
г) 4а2 + 20а + 25
2. Раскройте скобки (х + 5у)2
а) х2 — 10ху + 25у2
б) х2 + 10ху + 5у2
в) х2 + 10х + 25у2
г) х2 + 10ху + 25у2
3. (5в + 8а)(5в - 8а)
а) (8а + 5в)2
б) 64а2 — 25в2
в) 25в2 - 64а2
г) 25в2 — 8а2
4. Равенство верно или нет
(х + 4у)2 = х2 + 16у2 + 8ху
а) да
б) нет
Домашнее задание
1.Преобразуйте в многочлен:
а) (c + 7)2; в) (3x – 4)(3x + 4);
б) (5c – 2)2; г) (a 2 + 2)(a 2 – 2).
2.Разложите на множители:
а) – b 2; б) y 2 + 12y + 36.
3.Найдите значение выражения
(3x – y)2 – 3x(3x – 2y) при y = – .
4. Выполните действия:
а) 5(3mn + 1)(3mn – 1); в) (c – d)2 – (c + d)2.
б) (a 3 – b 4) 2;
5.Решите уравнение:
а) (5х – 1)(5х + 1) – (5x + 2)2 = 0;
б) 36b2 – 121 = 0.
Домашнее задание
1.Преобразуйте в многочлен:
а) (c + 7)2; в) (3x – 4)(3x + 4);
б) (5c – 2)2; г) (a 2 + 2)(a 2 – 2).
2.Разложите на множители:
а) – b 2; б) y 2 + 12y + 36.
3.Найдите значение выражения
(3x – y)2 – 3x(3x – 2y) при y = – .
4. Выполните действия:
а) 5(3mn + 1)(3mn – 1); в) (c – d)2 – (c + d)2.
б) (a 3 – b 4) 2;
5.Решите уравнение:
а) (5х – 1)(5х + 1) – (5x + 2)2 = 0;
б) 36b2 – 121 = 0.
Домашнее задание
1.Преобразуйте в многочлен:
а) (c + 7)2; в) (3x – 4)(3x + 4);
б) (5c – 2)2; г) (a 2 + 2)(a 2 – 2).
2.Разложите на множители:
а) – b 2; б) y 2 + 12y + 36.
3.Найдите значение выражения
(3x – y)2 – 3x(3x – 2y) при y = – .
4. Выполните действия:
а) 5(3mn + 1)(3mn – 1); в) (c – d)2 – (c + d)2.
б) (a 3 – b 4) 2;
5.Решите уравнение:
а) (5х – 1)(5х + 1) – (5x + 2)2 = 0;
б) 36b2 – 121 = 0.
Домашнее задание
1.Преобразуйте в многочлен:
а) (c + 7)2; в) (3x – 4)(3x + 4);
б) (5c – 2)2; г) (a 2 + 2)(a 2 – 2).
2.Разложите на множители:
а) – b 2; б) y 2 + 12y + 36.
3.Найдите значение выражения
(3x – y)2 – 3x(3x – 2y) при y = – .
4. Выполните действия:
а) 5(3mn + 1)(3mn – 1); в) (c – d)2 – (c + d)2.
б) (a 3 – b 4) 2;
5.Решите уравнение:
а) (5х – 1)(5х + 1) – (5x + 2)2 = 0;
б) 36b2 – 121 = 0.
Домашнее задание
1.Преобразуйте в многочлен:
а) (c + 7)2; в) (3x – 4)(3x + 4);
б) (5c – 2)2; г) (a 2 + 2)(a 2 – 2).
2.Разложите на множители:
а) – b 2; б) y 2 + 12y + 36.
3.Найдите значение выражения
(3x – y)2 – 3x(3x – 2y) при y = – .
4. Выполните действия:
а) 5(3mn + 1)(3mn – 1); в) (c – d)2 – (c + d)2.
б) (a 3 – b 4) 2;
5.Решите уравнение:
а) (5х – 1)(5х + 1) – (5x + 2)2 = 0;
б) 36b2 – 121 = 0.
Домашнее задание
1.Преобразуйте в многочлен:
а) (c + 7)2; в) (3x – 4)(3x + 4);
б) (5c – 2)2; г) (a 2 + 2)(a 2 – 2).
2.Разложите на множители:
а) – b 2; б) y 2 + 12y + 36.
3.Найдите значение выражения
(3x – y)2 – 3x(3x – 2y) при y = – .
4. Выполните действия:
а) 5(3mn + 1)(3mn – 1); в) (c – d)2 – (c + d)2.
б) (a 3 – b 4) 2;
5.Решите уравнение:
а) (5х – 1)(5х + 1) – (5x + 2)2 = 0;
б) 36b2 – 121 = 0.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.