Конспект урока "Признак параллельности прямых по равенству соответственных углов"

Повторив признак параллельности прямых по равенству накрест лежащих углов, переходим к  изучению признака параллельности прямых по равенству соответственных углов. Мы приводим  формулировку теоремы, доказываем её и решаем задачи. Конспект урока "Признак параллельности прямых по равенству соответственных углов"    Признак параллельности прямых по равенству накрест лежащих углов: Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. Теорема: Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. Доказательство: Пусть при пересечении прямых а и b секущей c соответственные углы 1 и 2 равны. Докажем, что прямая а параллельна прямой b. Заметим, что углы 2 и 3 равны, так как они являются вертикальными. Следовательно, ∠1=∠2, а ∠2=∠3, следует, что ∠1=∠3. А так как уголы 1 и 3 являются накрест лежащими  углами, образованными при пересечении прямых а и b секущей c, то в силу признака параллельности прямых по равенству накрест лежащих углов получаем, что прямая а параллельна прямой b. Теорема доказана. Пример. Прямая а параллельна прямой b. Прямая c - секущая при этих параллельных прямых. Найти все углы равные углу 1.∠1=∠5, так как это соответственные углы при параллельных прямых. Углы 1 и 1 равны как вертикальные. ∠5=∠7, так как они также являются вертикальными. А, следовательно, ∠1=∠7. 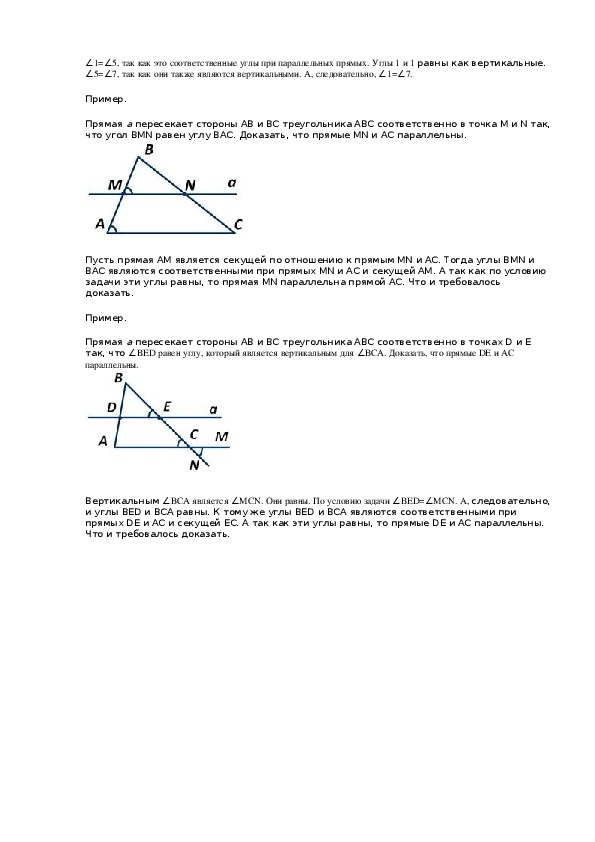Пример. Прямая а пересекает стороны АВ и ВС треугольника АВС соответственно в точка М и N так, что угол BMN равен углу ВАС. Доказать, что прямые MN и АС параллельны. Пусть прямая АМ является секущей по отношению к прямым MN и АС. Тогда углы BMN и ВАС являются соответственными при прямых MN и АС и секущей АМ. А так как по условию задачи эти углы равны, то прямая MN параллельна прямой АС. Что и требовалось доказать. Пример. Прямая а пересекает стороны АВ и ВС треугольника АВС соответственно в точках D и E так, что ∠BED равен углу, который является вертикальным для ∠ВСА. Доказать, что прямые DE и АС  параллельны. Вертикальным ∠ВСА является ∠MCN. Они равны. По условию задачи ∠BED=∠MCN. А, следовательно, и углы BED и ВСА равны. К тому же углы BED и ВСА являются соответственными при прямых DE и АС и секущей ЕС. А так как эти углы равны, то прямые DE и АС параллельны. Что и требовалось доказать.