
Использование графиков функций при решении уравнений.
Конспект 1 урока.
Тема: «Графическое решение уравнений».
Ребята, наши занятия будут посвящены изучению графического метода решения уравнений. Но этот метод не является для вас совсем новым, т.к. на уроках математики вы уже рассматривали графическое решение некоторых уравнений.
Графики часто облегчают нахождение решений, сокращая и упрощая аналитические выкладки, позволяют определить число корней, угадать значения корня, а иногда и вовсе являются единственным методом решения уравнений. Использование хотя бы схематических графических иллюстраций помогает определить направление исследований, а иногда и сразу подобрать ключ к решению задачи. Но для успешного овладения данным методом, необходимы знания элементарных функций, а также умение их строить и преобразовывать.
На наших занятиях мы закрепим ваше умение строить графики функций с помощью элементарных преобразований, поближе познакомимся с графическим методом решения уравнений, рассмотрим решение более сложных задач и научимся решать уравнения с параметрами.
Так в чем же заключается графический метод? А заключается он в следующем: для того, чтобы решить уравнение с одним неизвестным графическим методом нужно:
1.
Это уравнение
записать в виде ![]() и рассмотреть систему
и рассмотреть систему 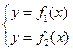
2.
В одной системе
координат построить графики функций ![]() и
и ![]() .
.
3. Найти точки пересечения графиков. Абсциссы их равны корням исходного уравнения. Если таких точек нет, то уравнение не имеет решений.
4. Если корень нашелся, то сделать проверку, т.е. подставить его в уравнение и проверить справедливость равенства.
Последний пункт является очень важным, т.к. мы строим эскизы графиков функций, следовательно, мы не можем назвать точные значения координат точек пересечения, мы можем только предполагать и догадываться о каких-либо значениях, поэтому проверка просто необходима.
Рассмотрим данный метод на примере.
Пример №1. Решить уравнение ![]() .
.
Будем следовать нашему плану.
Во-первых, запишем данное уравнение в
виде ![]() и рассмотрим систему
и рассмотрим систему 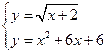 .
.
Во-вторых, в одной системе координат
изобразим графики данных функций. Замечаем, что график функции ![]() может быть получен из графика функции
может быть получен из графика функции ![]() сдвигом на 2 единицы влево, а сам график представляет собой
одну ветвь параболы.
сдвигом на 2 единицы влево, а сам график представляет собой
одну ветвь параболы.
|
|
Вторая функция есть квадратный
трехчлен ![]() , графиком ее является парабола. Есть 2 способа
построения графика данной функции:
, графиком ее является парабола. Есть 2 способа
построения графика данной функции:
1) определить координаты вершины и затем построить параболу по шаблону;
2)
выделить полный
квадрат и затем, последовательно выполняя элементарные преобразования над
графиком функции ![]() , построить график данной функции.
, построить график данной функции.
|
|
Воспользуемся
2-ым способом. ![]()
![]()
Видим, что график функции ![]() нужно сдвинуть на 3 единицы влево и
на 3 единицы вниз.
нужно сдвинуть на 3 единицы влево и
на 3 единицы вниз.
|
|
Наши графики пересеклись в одной точке, следовательно, будет только одно решение. Абсцисса данной точки равна -1, это и есть наш предполагаемый корень. Теперь нужно обязательно сделать проверку.
![]()
В левой части получили ноль, значит наше равенство верно и -1 является корнем данного уравнения.
Ответ: -1
Рассмотрим еще несколько примеров.
Пример №2. Решить уравнение ![]() .
.
Заметим,
что данное уравнение уже записано в нужном для нас виде, поэтому рассмотрим систему
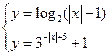 .
.
Теперь нам необходимо графики данных функций построить в одной системе координат.
Ребята,
посмотрите внимательно на первую функцию ![]() , как вы думаете, из графика какой
функции она может быть получена? Правильно, из графика функции
, как вы думаете, из графика какой
функции она может быть получена? Правильно, из графика функции ![]() с помощью последовательных элементарных
преобразований:
с помощью последовательных элементарных
преобразований:
|
|
1) y = log2(x-1) -
график функции ![]() сдвинем вправо на 1 единицу
сдвинем вправо на 1 единицу
2) ![]() - сохраним график функции при х > 0 и отразим его
симметрично относительно оси Оу .
- сохраним график функции при х > 0 и отразим его
симметрично относительно оси Оу .
Рассмотрим вторую функцию
![]() . Ее можно немного преобразовать:
. Ее можно немного преобразовать:
![]()
|
|
![]()
Заметим, что график данной
функции может быть построен с помощью простейших элементарных преобразований
графика функции ![]()
|
|
1) Построим график
функции ![]() - для этого сдвинем график функции
- для этого сдвинем график функции ![]() на 5 единиц влево.
на 5 единиц влево.
2) Построим график функции ![]() . Что нам для этого нужно сделать?
. Что нам для этого нужно сделать?
·
часть графика
функции ![]() при
при ![]() сохраняем;
сохраняем;
·
часть графика
функции при ![]() не рассматриваем;
не рассматриваем;
·
симметрично
отражаем часть графика функции ![]() при
при ![]() относительно оси Оу.
относительно оси Оу.
3) Построим график
функции ![]() - для этого сдвинем график
- для этого сдвинем график
|
|
функции ![]() на 1 единицу вверх.
на 1 единицу вверх.
Полученные графики функций пересекаются в двух точках, значит уравнение имеет 2 решения. Абсциссы точек равны 5 и -5, это наши предполагаемые корни. Остается их только проверить:
![]()
![]()
![]() , равенство верно, следовательно, 5 является корнем
уравнения.
, равенство верно, следовательно, 5 является корнем
уравнения.
![]()
![]()
![]() , равенство верно, следовательно, -5
является корнем уравнения.
, равенство верно, следовательно, -5
является корнем уравнения.
Ответ: 2 и -2
Рассмотрим следующий пример.
Пример №3. Решить уравнение ![]()
Запишем данное уравнение
в виде ![]() и рассмотрим систему:
и рассмотрим систему: 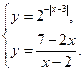
|
|
Теперь наша задача
состоит в том, чтобы построить графики данных функций в одной системе координат
![]() и
и ![]() .
.
Ребята, посмотрите внимательно на 1-ую функцию ![]() , как ее можно преобразовать? Правильно, можно воспользоваться
свойством степени, и записать данную функцию в виде
, как ее можно преобразовать? Правильно, можно воспользоваться
свойством степени, и записать данную функцию в виде ![]() . Ребята, как вы думаете из графика какой функции можно
получить график данной функции? Правильно, из графика функции
. Ребята, как вы думаете из графика какой функции можно
получить график данной функции? Правильно, из графика функции ![]() . Давайте теперь запишем с вами эту последовательность
элементарных преобразований:
. Давайте теперь запишем с вами эту последовательность
элементарных преобразований:
1) Строим график функции ![]()
2) ![]() -
график функции
-
график функции ![]() при x < 0 не
рассматриваем, а часть графика при
при x < 0 не
рассматриваем, а часть графика при ![]() отражаем симметрично относительно оси Оу.
отражаем симметрично относительно оси Оу.
3) ![]() -
сдвигаем график функции
-
сдвигаем график функции ![]() вправо на 3 единицы.
вправо на 3 единицы.
Рассмотрим
вторую функцию ![]() . Как ее можно преобразовать? Правильно, выделим целую часть, для
этого в числителе выразим наш знаменатель и почтенно поделим
. Как ее можно преобразовать? Правильно, выделим целую часть, для
этого в числителе выразим наш знаменатель и почтенно поделим
|
|
![]()
![]()
Составим цепочку элементарных преобразований:
1) ![]() Графиком обратной пропорциональности
является гипербола.
Графиком обратной пропорциональности
является гипербола.
|
|
2) ![]()
3) ![]() - график функции
- график функции ![]()
сдвинем вправо на 2 единицы.
4) ![]() - график функции
- график функции
![]() сдвинем вниз на 2 единицы.
сдвинем вниз на 2 единицы.
|
|
Видим, что данные графики пересекаются в 1 точке, следовательно, уравнение имеет только 1 решение. Абсцисса данной точки равна 3, это наш предполагаемый корень.
Сделаем проверку:
![]()
В левой части получили 0, значит, 0 = 0, равенство верно и 3 является корнем данного уравнения.
Ответ: 3
|
|
Самостоятельная работа.
Решить
уравнение ![]() .
.
Проверка самостоятельной работы:
1.
Запишем данное
уравнение в виде ![]() и рассмотрим систему
и рассмотрим систему 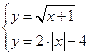
|
|
|
|
2.
Построим в одной
системе координат графики функций ![]() и
и ![]() . График первой функции
. График первой функции ![]() представляет собой одну ветвь параболы, полученной из графика
функции
представляет собой одну ветвь параболы, полученной из графика
функции ![]() сдвигом влево на 1 единицу. График второй функции
можно получить, построив прямую
сдвигом влево на 1 единицу. График второй функции
можно получить, построив прямую ![]() и отразив симметрично ее часть при x > 0 относительно оси Оу.
и отразив симметрично ее часть при x > 0 относительно оси Оу.
3. Полученные 2 графика пересекаются в одной точке, следовательно, уравнение имеет только 1 корень.
4. Абсцисса точки пересечения равна 3, убедимся, что 3 является корнем уравнения, сделав проверку:
![]() .
.
В левой части получили -4, значит -4 = -4, равенство верное и 3 является корнем данного уравнения.
Ответ: 3
Конспект 2 урока.
Тема: «Графический метод решения уравнений с параметрами».
Ребята, на этом занятии мы научимся решать графическим методом уравнения с параметрами. Но прежде выясним, какие уравнения называются уравнениями с параметром и чем они отличаются от обычных уравнений.
Ранее мы с
вами решали уравнения с одной неизвестной, например ![]() .
Но если в уравнение наряду с этой неизвестной величиной входит неизвестное, но
фиксированное число, обозначаемое буквой, то оно называется параметром, а само
уравнение называется параметрическим. Приведем пример таких уравнений
.
Но если в уравнение наряду с этой неизвестной величиной входит неизвестное, но
фиксированное число, обозначаемое буквой, то оно называется параметром, а само
уравнение называется параметрическим. Приведем пример таких уравнений ![]() , здесь а выступает в
качестве параметра. Еще со времён Декарта последними буквами латинского
алфавита x, у и z обычно обозначают переменные, а
первыми a, b и c – параметры. Это позволяет во многих
случаях не указывать, какой буквой обозначен параметр, а какой – переменная.
, здесь а выступает в
качестве параметра. Еще со времён Декарта последними буквами латинского
алфавита x, у и z обычно обозначают переменные, а
первыми a, b и c – параметры. Это позволяет во многих
случаях не указывать, какой буквой обозначен параметр, а какой – переменная.
Решить уравнение с параметром значит, для каждого значения параметра указать множество решений данного уравнения. При решении таких уравнений особенно эффективен графический метод. Он заключается в следующем:
1.
Записываем уравнение
в виде ![]() и рассматриваем систему
и рассматриваем систему 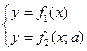
Так же мы поступали и при графическом решении обычных уравнений.
2. Затем строим графики данных функций, но все различие состоит в том, что функция y = f2(x;a) задает не одну кривую, а семейство кривых, зависящих от параметра а. Пересекая такими кривыми график функции y = f1(x), получим при различных значениях а различные точки пересечения графиков.
3. Количество точек пересечения равно количеству решений уравнения при конкретном значении а.
Рассмотрим решение таких уравнений на примере.
Пример 1. При каких значениях параметра а
уравнение ![]() имеет ровно 3 корня.
имеет ровно 3 корня.
Решение: Перенесем 2-ой модуль в правую часть
и запишем данное уравнение в виде ![]() ,
рассмотрим систему
,
рассмотрим систему 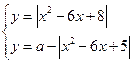 .
.
|
|
Нам
нужно построить графики данных функций в одной системе координат, рассмотрим
первую из них ![]() . Построим сначала график
функции
. Построим сначала график
функции ![]() , а затем
, а затем ![]() . Ребята, что представляет собой
график квадратного трехчлена и как его построить? Правильно, графиком
квадратного трехчлена является парабола и для того, чтобы построить ее выделим
полный квадрат:
. Ребята, что представляет собой
график квадратного трехчлена и как его построить? Правильно, графиком
квадратного трехчлена является парабола и для того, чтобы построить ее выделим
полный квадрат:
|
|
![]()
![]()
Теперь мы видим, что для
того, чтобы получить график функции ![]() , нужно график
функции
, нужно график
функции ![]() сдвинуть на 3 единицы вправо и на 1 единицу вниз.
сдвинуть на 3 единицы вправо и на 1 единицу вниз.
Ребята,
как построить график функции ![]() , если известен
график функции
, если известен
график функции ![]() ? Правильно,
? Правильно,
1) сохраним часть графика функции, лежащую выше оси Ох;
2) часть графика функции, лежащую ниже оси Ох, отразить симметрично относительно нее.
|
|
Теперь рассмотрим 2-ую
функцию ![]() . Так как она содержит параметр, значит, задает
семейство кривых. Ребята, что это будут за кривые и, подумайте, как будет
выглядеть цепочка элементарных преобразований. Правильно, данная функция задает
семейство парабол, поэтому для их построения выделим полный квадрат
. Так как она содержит параметр, значит, задает
семейство кривых. Ребята, что это будут за кривые и, подумайте, как будет
выглядеть цепочка элементарных преобразований. Правильно, данная функция задает
семейство парабол, поэтому для их построения выделим полный квадрат
![]()
![]()
|
|
Видим, что для того,
чтобы построить график функции ![]() нужно график функции
нужно график функции ![]() сдвинуть на 3 единицы вправо и 4 единицы вниз. Значит, наша
цепочка элементарных преобразований будет выглядеть так:
сдвинуть на 3 единицы вправо и 4 единицы вниз. Значит, наша
цепочка элементарных преобразований будет выглядеть так:
1) ![]()
2) ![]() - сдвиг вправо на 3 единицы
- сдвиг вправо на 3 единицы
3) ![]() - сдвиг вниз на 4 единицы
- сдвиг вниз на 4 единицы
4) ![]()
5) ![]()
6) ![]()
|
|
Ребята,
как построить график функции ![]() , если известен график функции
, если известен график функции ![]() ? Правильно, сохраняем часть графика функции, лежащую выше
оси Ох, а часть графика функции
? Правильно, сохраняем часть графика функции, лежащую выше
оси Ох, а часть графика функции ![]() , лежащую ниже оси Ох, отражаем
симметрично относительно нее.
, лежащую ниже оси Ох, отражаем
симметрично относительно нее.
Теперь
зная график функции ![]() нам нужно построить график функции
нам нужно построить график функции ![]() . Ребята, как нам это сделать? Правильно, для этого график
функции
. Ребята, как нам это сделать? Правильно, для этого график
функции ![]() нужно симметрично отразить относительно оси Ох.
нужно симметрично отразить относительно оси Ох.
График
последней функции получим, если сдвинем график функции ![]() на а единиц вверх при a > 0, и на а единиц вниз, при a < 0.
на а единиц вверх при a > 0, и на а единиц вниз, при a < 0.
Из рисунка видим, что три точки пересечения будет только при а = 5. А значит, уравнение будет иметь 3 корня при а = 5.
Ответ: а = 5
Пример 2. При всех значениях параметра а
решить уравнение ![]() .
.
|
|
Решение: Рассмотрим систему уравнений 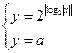 .
.
Видим, что вторая функция задает семейство прямых параллельных оси Ох.
А для того, чтобы
построить график первой функции, рассмотрим сначала ее поведение при х >
0. Функция на этом интервале примет вид 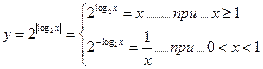 .
.
Т.е. ее график состоит из
2-х частей: гиперболы при 0 < x < 1, и прямой при x > 1. Изобразим их на координатной
прямой. Ребята, скажите, как нам построить график функции ![]() , если нам известен график функции
, если нам известен график функции ![]() . Правильно, при построении графика данной функции следует
учесть, что она является четной, т.е. ее график симметричен относительно оси
Оу. Поэтому сохраним график функции при x > 0 и отразим его симметрично
относительно оси Оу.
. Правильно, при построении графика данной функции следует
учесть, что она является четной, т.е. ее график симметричен относительно оси
Оу. Поэтому сохраним график функции при x > 0 и отразим его симметрично
относительно оси Оу.
|
|
Теперь будем пересекать полученный график функции прямыми параллельными оси Ох. Видим, что при а < 1 уравнение не имеет решений, при а = 1 уравнение имеет 2 решения, при а > 1 уравнение имеет 4 решения.
Ответ: при а < 1 уравнение не имеет решений;
при а = 1 уравнение имеет 2 решения;
при а > 1 уравнение имеет 4 решения.
Графический метод не всегда позволяет до конца решить уравнение, иногда приходится использовать и другие методы. Рассмотрим такой пример.
Пример 3. При каких значениях параметра а
уравнение ![]() имеет единственное решение.
имеет единственное решение.
|
|
Решение:
Запишем данное уравнение
в виде ![]() и рассмотрим систему
и рассмотрим систему 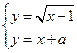 .
.
Графиком первого уравнения
![]() является одна ветвь параболы,
полученная из графика функции
является одна ветвь параболы,
полученная из графика функции ![]() сдвигом вправо на 1 единицу.
сдвигом вправо на 1 единицу.
Графиком второй функции является семейство параллельных прямых. При различных а прямые различны, например:
При ![]() :
: ![]()
|
|
При ![]() :
: ![]()
При ![]() :
: ![]()
При ![]() :
: ![]()
При ![]() :
: ![]()
При ![]() :
: ![]()
|
|
При ![]() :
: ![]() и
т.д.
и
т.д.
И из рисунка видно, что если а < -1, то графики будут пересекаться в одной точке, а, следовательно, уравнение будет иметь единственное решение.
Еще один случай, когда
графики имеют одну общую точку, это когда прямая у = х + а касается
графика функции ![]() . Но графически точные
значения параметра а мы при этом определить не можем. Будем
пользоваться в этом случае
. Но графически точные
значения параметра а мы при этом определить не можем. Будем
пользоваться в этом случае ![]() . Ребята, под каким углом проходят
прямые у = х + а к положительному направлению оси Ох? Правильно, под
углом 450. А чему равен tg450? tg450 = 1. Следовательно,
. Ребята, под каким углом проходят
прямые у = х + а к положительному направлению оси Ох? Правильно, под
углом 450. А чему равен tg450? tg450 = 1. Следовательно, ![]() . Найдем значение производной в данной точке
. Найдем значение производной в данной точке ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
Найдем значение функции в данной точке.
![]()
Мы получили, что точка пересечения имеет координаты (1,25; 0,5). Следовательно, должно выполняться следующее равенство: 0,5 = 1,25 + а
а = -0, 75.
Значит, наше уравнение имеет единственное решение при а < -1 и при а = -0,75.
Ответ: ![]()
Самостоятельная работа.
Определите, при каком значении параметра
а уравнение ![]() имеет ровно три
различных действительных корня.
имеет ровно три
различных действительных корня.
|
|
Проверка самостоятельной работы:
Рассмотрим следующую систему 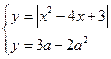 . Ребята, как нам построить график 1-ой функции
. Ребята, как нам построить график 1-ой функции ![]() ?
?
Правильно, построим сначала
параболу ![]() . Для этого выделим полный квадрат
. Для этого выделим полный квадрат ![]() ,
, ![]() . Теперь видим, что для получения
нашего графика нужно сдвинуть параболу
. Теперь видим, что для получения
нашего графика нужно сдвинуть параболу ![]() вправо на 2 единицы и вниз на 1
единицу. Затем сохраним часть графика, лежащую выше оси Ох, а часть графика, лежащую
ниже оси Ох, отразим симметрично относительно нее и получим график
функции
вправо на 2 единицы и вниз на 1
единицу. Затем сохраним часть графика, лежащую выше оси Ох, а часть графика, лежащую
ниже оси Ох, отразим симметрично относительно нее и получим график
функции ![]() .
.
Теперь
рассмотрим вторую функцию ![]() . Т.к. она содержит параметр, значит,
задает семейство кривых, а в нашем случае – семейство прямых, параллельных оси Ох.
. Т.к. она содержит параметр, значит,
задает семейство кривых, а в нашем случае – семейство прямых, параллельных оси Ох.
Из рисунка видим, что 3
точки пересечения, а значит и 3 решения уравнения, будет только при ![]() . Решаем получившееся квадратное уравнение и получаем, что а
= 0,5 и а = 1.
. Решаем получившееся квадратное уравнение и получаем, что а
= 0,5 и а = 1.
Ответ: а = 0,5 и а = 1.
Конспект урока 3
Тема: "Координатно-параметрический метод".
Ребята, на прошлом занятии мы рассматривали графическое решение уравнении с параметрами, давайте вспомним в чем заключается суть этого метода? Ребята отвечают.
Сегодня на занятии мы познакомимся с еще одном графическим методом решения уравнений с параметрами - координатно – параметрическим. Чем же этот метод отличается от уже изученного нами метода? А вот чем: раньше мы строили графики в системе координат хОу, но порой бывает намного удобнее и проще построить графики в системе координат хОа или аОх, где х – координата, а – параметр. Такие плоскости называются координатно – параметрическими, а сам метод - координатно – параметрическим. Число решений уравнения при каждом фиксированном значении параметра а равно количеству точек пересечения кривой с горизонтальной прямой, соответствующей этому значению параметра.
Рассмотрим применение данного метода на примерах.
Пример 1. Найти все значения а, при каждом из которых уравнение
![]() имеет ровно 3 различных корня.
имеет ровно 3 различных корня.
|
|
Решение: Ребята, когда произведение равно
нулю? Правильно, когда один из множителей равен нулю, поэтому данное уравнение
равносильно совокупности двух уравнений 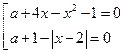 .
Ребята, при решении уравнений
мы всегда можем применять равносильные преобразования и рассматривать не
уравнение, а, например, системы или совокупности.
.
Ребята, при решении уравнений
мы всегда можем применять равносильные преобразования и рассматривать не
уравнение, а, например, системы или совокупности.
Немного преобразуем данную
совокупность 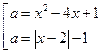 . Мы выразили параметр а как функцию от х,
графики таких функций намного удобнее строить в системе координат хОа, а не в
хОу, что мы и сделаем.
. Мы выразили параметр а как функцию от х,
графики таких функций намного удобнее строить в системе координат хОа, а не в
хОу, что мы и сделаем.
Рассмотрим
первую функцию ![]() . Что является графиком данной функций? Конечно
парабола. Выделим полный квадрат
. Что является графиком данной функций? Конечно
парабола. Выделим полный квадрат ![]()
![]()
|
|
Видим, что для того,
чтобы построить график функции ![]() , нужно график функции
, нужно график функции ![]() сдвинуть на 2 единицы вправо и 3 единицы вниз.
сдвинуть на 2 единицы вправо и 3 единицы вниз.
Рассмотрим
2-ую функцию. Ребята, подумайте какую цепочку элементарных преобразований нужно
проделать, чтобы построить график данной функции ![]() .
.
1) ![]()
2) ![]() - сдвиг графика функции
- сдвиг графика функции ![]()
вправо на 2 единицы
|
|
3) ![]() - сдвиг графика функции
- сдвиг графика функции ![]()
вниз на 1 единицу
Таким образом, 2 графика
функций ![]() и
и ![]() изображены в одной системе координат аОх.
И теперь мы будем искать не точки пересечения графиков, а пересекать данные
графики прямыми параллельными оси Ох. Каждая из них соответствует определенному
значению параметра а. Та прямая, которая пересечет данные графики в 3-х
точках и даст нам решение. В нашем случае только прямая а = -1
пресекает данные графики функций в 3-х точках. Следовательно, уравнение имеет
3 различных положительных корня только при а = -1.
изображены в одной системе координат аОх.
И теперь мы будем искать не точки пересечения графиков, а пересекать данные
графики прямыми параллельными оси Ох. Каждая из них соответствует определенному
значению параметра а. Та прямая, которая пересечет данные графики в 3-х
точках и даст нам решение. В нашем случае только прямая а = -1
пресекает данные графики функций в 3-х точках. Следовательно, уравнение имеет
3 различных положительных корня только при а = -1.
Ответ: а = -1.
Пример 2. Для
каждого значения параметра а решить уравнение ![]() .
.
Решение: Рассмотрим
систему 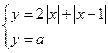 . Для того, чтобы построить график первой функции, заменим уравнение
. Для того, чтобы построить график первой функции, заменим уравнение ![]() совокупностью
3-х систем.
совокупностью
3-х систем.
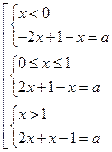
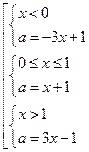
Значит, график данной функции состоит из 3 частей: при x < 0, 0 < x <1 и x >1. Т. к. параметр а мы выразили как функцию от х, то график данной функции будет удобно строить на КП- плоскости хОа на указанных интервалах.
Рассмотрим
вторую функцию. Она задает семейство параллельных прямых. Будем пересекать ими
график функции ![]() . Количество точек пересечения при заданном значении
параметра является числом решений уравнения.
. Количество точек пересечения при заданном значении
параметра является числом решений уравнения.
Ответ: Если ![]() ,
то
,
то ![]()
Если ![]() ,
то
,
то ![]() и
и ![]()
Если ![]() ,
то
,
то ![]() и
и ![]()
Но не всегда параметр а нужно выражать как функцию от х и строить графики на КП- плоскости хОа, иногда удобнее представить х как функцию зависящую от параметра, в этом случае графики строятся на КП- плоскости аОх. Рассмотрим такой пример.
Пример 2: Найдите все значения параметра а,
при которых уравнение имеет одно решение 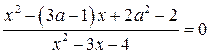
Решение: Ребята, когда дробь равна
нулю? Правильно, когда числитель равен нулю. А что нужно сказать про
знаменатель дроби? Правильно, он должен быть отличным от нуля. Поэтому данное
уравнение равносильно системе 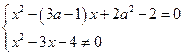
Решим первое уравнение системы относительно а.
![]()
![]()
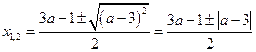
Если ![]() , то
, то ![]() и
и ![]()
|
|
Если ![]() , то получим те же самые корни.
, то получим те же самые корни.
Решим второе уравнение системы ![]() .
.
По теореме Виета получаем, что ![]() и
и ![]() .
.
Поэтому данное уравнение равносильно
системе 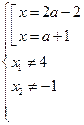
Так как неизвестная х является функцией от параметра а, то графики данных функций удобно построить в системе координат аОх, т.е. на КП–плоскости аОх. Выкалим на этих графиках точки с ординатой равной 4 и -1.
Теперь
пересекаем графики данных функций вертикальными прямыми. Заметим, что именно
наличие проколов в графиках позволяют при а = -2 и ![]() иметь уравнению единственное решение.
иметь уравнению единственное решение.
Ответ: а = -2 и ![]()
Самостоятельная работа.
Пример. При каких значениях параметра а уравнение ![]() имеет
2 корня?
имеет
2 корня?
|
|
|
|
Решение: Наше уравнение равносильно системе 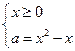 .
.
Так как параметр а
является функцией от х, то график данной функции ![]() удобнее построить в системе координат хОа. Он
представляет собой параболу, но нас будет интересовать только часть параболы
при
удобнее построить в системе координат хОа. Он
представляет собой параболу, но нас будет интересовать только часть параболы
при ![]() .
.
Выделим полный квадрат:
![]()
![]()
Видим, что для того,
чтобы построить график функции ![]() , нужно график функции
, нужно график функции ![]() сдвинуть на
сдвинуть на ![]() единиц вправо и
единиц вправо и ![]() единиц вниз.
единиц вниз.
Затем
будем пересекать полученный график прямыми параллельными оси Ох, каждая из
которых соответствует конкретному значению параметра а. Число решений
уравнения при каждом фиксированном значении параметра а равно количеству
точек пересечения кривой с горизонтальной прямой, соответствующей этому
значению параметра. Поэтому из рисунка видно, что при ![]() , уравнение будет иметь 2 точки
пересечения, а значит и 2 корня.
, уравнение будет иметь 2 точки
пересечения, а значит и 2 корня.
Ответ: ![]()
Литература:
1. Горнштейн П. И., Полонский В.Б., Якир М.С. Задачи с параметрами. ИЛЕКСА,
Москва, 2007
2. Моденов В.П. Задачи с параметрами. Координатно-параметрический метод.
ЭКАМЕН, Москва, 2007
3. Кремер Н.Ш. Математика для поступающих в вузы. ЮНИТИ, Москва, 2008
4. Крамор В.С. Задачи с параметрами и методы их решения. ОНИКС, Москва, 2007
5. Талочкин П.Б. Неравенства и уравнения. Упражнения и методические указания.
Просвещение, Москва, 1970
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.