_Квадратные уравнения_Методические рекомендации к уроку №2

Методические рекомендации к проведению урока

Тема урока: Повторение раздела «Квадратные уравнения»

Тип урока: урок-повторение

Цели обучения:

8.2.2.1

знать определение квадратного уравнения;

8.2.2.2

различать виды квадратных уравнений;

8.2.2.3

решать квадратные уравнения;

8.2.2.4

применять теорему Виета;

8.2.1.1

усвоить понятие корня квадратного трехчлена;

8.2.1.2

выделять полный квадрат двучлена из трехчлена;

8.2.1.3

раскладывать квадратный трехчлен на множители;

8.2.2.5

решать уравнения вида |ax2+bx|+c=0; ax2+b|x|+c=0;

8.2.2.6

решать дробно-рациональные уравнения;

8.2.2.7

решать уравнения, приводимые к квадратным уравнениям;

8.4.2.1

решать текстовые задачи с помощью квадратных уравнений;

8.4.2.2

решать текстовые задачи с помощью дробно-рациональных уравнений;

Цели урока:

·         Решать квадратные уравнения различными методами: с помощью формул, с помощью теоремы Виета, путем выделения полного квадрата двучлена;

·         Решать уравнения, приводимые к квадратным уравнениям (биквадратные уравнения, дробно-рациональные уравнения);

·         Решать текстовые задачи с помощью квадратных и дробно-рациональных уравнений.

Структура урока

1.    Организационный момент. Целеполагание.

2.    Повторение.

3.    Решение задач практического содержания.

4.    Тест за раздел «Квадратные уравнения».

5.    Самостоятельная работа по теме «Квадратные и дробно-рациональные уравнения».

6.    Подведение итогов урока. Рефлексия.

Теоретический материал к уроку, определения к понятиям и др.

Алгоритм решения уравнения ах²+bх+с=0:

1.  Вычислить дискриминант D по формуле

D = b² - 4ас.

2. Если D < 0, то квадратное уравнение не имеет действительных корней.

3. Если D = 0, то квадратное уравнение имеет один корень:

4. Если D > 0, то квадратное уравнение имеет два корня:

Теорема.  Если х₁  и  х₂   –   корни  квадратного  трехчлена а х² + bx + c, то

а х² + bx + c = а(х - х₁)(х - х₂ ).

Схема решения дробно-рациональных уравнений:

1.      Найти общий знаменатель дробей, входящих в уравнение.

2.      Умножить обе части уравнения на общий знаменатель.

3.      Решить получившееся уравнение.

4.      Исключить из его корней те числа, которые обращают в нуль общий знаменатель.

Инструкции к демонстрациям и технике безопасности.

Демонстрация материала осуществляется с помощью презентации PowerPoint. Слайды презентации содержат анимации, которые позволяют поэтапно вывести на экран решения и ответы к предложенным заданиям. Поэтому при показе презентации следует делать паузы после демонстрации заданий и постановки вопросов, давая учащимся время на их выполнение и обдумывание ответов.

Дополнительные методические рекомендации по организации урока.

Структура и организация урока нацелены на продуктивную деятельность учащихся при изучении новой темы, не допуская пассивного восприятия материала. В связи с этим учителю необходимо задавать учащимся вопросы высокого порядка, наталкивая их на «открытие» и освоение нового материала, при этом выдерживая паузы, необходимые для обдумывания.    

Дополнительные разноуровневые (на дифференциацию) задания.

Базовый уровень

1.      Сократите дробь

2.      Решите уравнение

Продвинутый уровень

1.      Не вычисляя корней квадратного уравнения , найдите.

2.      При каком значении а квадратный трехчлен можно разложить на линейные множители

3.      Решите уравнение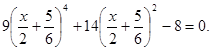

Рекомендации по формативному оцениванию.

Формативное оценивание производится на каждом этапе урока (самооценивание, взаимооценивание, оценивание учителем по критериям). Оценка путем наблюдения за вовлечением учеников в работу при выполнении заданий и за участием в диалогах. Прогресс, ответную реакцию на задания в парах, в группах необходимо отслеживать для того, чтобы оценить вклад каждого ученика и выявить наличие ошибок для их дальнейшей коррекции.

Ответы, критерии к заданиям, дополнительные материалы к уроку.

Ответы к заданиям будут полезны для организации самооценивания или взаимооценивания учащихся.

Ответы к приложению 1.

Ключевое слово – НИКЕЛЬ.

Ответы к приложению 2.

Вариант 1.

1.      1) нет действительных корней. 2) 25.

2.      4; 5.

3.      6.

4.      .

Вариант 2.

1.      1) нет действительных корней. 2) 0,6 и 2.

2.      3; 4.

3.      -11.

4.      .

Критерии оценивания к каждому блоку заданий прописаны в приложениях к уроку, а также указаны в краткосрочном плане.

Список полезных ссылок и литературы.

Алгебра. 8-класс: Учебник для 8 класса общеобразовательной школы с русским языком обучения/ А.Н. Шыныбеков – 3-издание. – Алматы: «Атамұра», 2012. 288 с.

Алгебра. 8-класс: Учебник для 8 класса общеобразовательной школы с русским языком обучения/ А.Е. Абылкасымова – Алматы: «Мектеп», 2008. 144 с.

Алгебра. Дидактический материал 9 класс. Учебное пособие для 9 классов 12-летних школ. Алматы «Мектеп», 2011 Авторы: В.Е.Корчевский, А.А.Малая, Я.С.Первушина

Алгебра. 9  класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 21-е изд., испр. — М. : Мнемозина,

2014.