Лекция №8: «Автоматическая обработка информации»

Цель занятия: изучить понятие и структуру автоматической обработки информации.

 Дидактическая – формирование мотивации и опыта учебнопознавательной и практической деятельности. Создание условий для обобщения и систематизации знаний, проверка ЗУН. 

 Развивающая - способствовать формированию памяти, находчивости, научного мировоззрения.

Воспитательная - развивать логическое мышление и умение выражать речью результаты собственной мыслительной деятельности. Способствовать развитию умению анализировать, выдвигать гипотезы, предложения. 

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1.  Семакин И.Г. Информатика: учебник для 10 кл. / И.Г. Семакин, Е.К.

Хеннер, Шеина Т.Ю.– М.: Изд-во "БИНОМ. Лаборатория знаний", 2015. – 264с.

2.  Семакин И.Г. Основы программирования: учебник./ Семакин И.Г., А.П. Шестаков– М.: Мастерство, 2002. – 432 с. ISBN 5-294-00054-7

3.  Михеева Е.В. Информационные технологии в информационной деятельности / Е.В. Михеева. -  9-е изд., стер. – М.: Издательский центр «Академия», 2010. – 384 с.

План

1.     Понятие автоматической обработки информации.

2.     Поиск данных. Постановка задачи поиска данных.

3.     Организация набора данных. Последовательный поиск.

1.Понятие автоматической обработки информации

В качестве примера автомата, выполняющего обработку информации, рассмотрим машину Э. Поста. Алгоритм, по которому работает машина Поста, будем называть программой.

Договоримся о терминологии: под словом «программа» мы всегда будем понимать алгоритм, записанный по строгим правилам языка команд исполнителя — на языке программирования для данного исполнителя.

Опишем архитектуру машины Поста (рис. 1). Имеется бесконечная информационная лента, разделенная на позиции — клетки. В каждой клетке может либо стоять метка (некоторый знак), либо отсутствовать (пусто)

Рис. 1. Модель машины Поста

Вдоль ленты движется каретка — считывающее устройство. На рисунке она обозначена стрелкой. Каретка может передвигаться шагами: один шаг — смещение на одну клетку вправо или влево. Клетку, под которой установлена каретка, будем называть текущей.

Каретка является еще и процессором машины. С ее помощью машина может:

• распознать, пустая клетка или помеченная знаком;

• стереть знак в текущей клетке;

• записать знак в пустую текущую клетку.

Если произвести замену меток на единицы, а пустых клеток — на нули, то информацию на ленте можно будет рассматривать как аналог двоичного кода телеграфного сообщения или данных в памяти компьютера. Существенное отличие каретки-процессора машины Поста от процессора компьютера состоит в том, что в компьютере возможен доступ процессора к ячейкам памяти в произвольном порядке, а в машине Поста — только последовательно.

Назначение машины Поста — производить преобразования на информационной ленте. Исходное состояние ленты можно рассматривать как исходные данные задачи, конечное состояние ленты — результат решения задачи. Кроме того, в исходные данные входит информация о начальном положении каретки.

                                  2.        Поиск данных. Постановка задачи поиска данных

Вспомните, как часто приходится вам искать какие-нибудь данные. Таких примеров много и в бытовых ситуациях, и в учебном процессе. Например, в программе телепередач вы ищете время начала трансляции футбольного матча; в расписании поездов — сведения о поезде, идущем до нужной вам станции. На уроке физики, решая задачу, ищете в таблице удельный вес меди. На уроке английского языка, читая иностранный текст, ищете в словаре перевод слова на русский язык. Работая за компьютером, вам нередко приходится искать на его дисках файлы с нужными данными или программами.

Постановка задачи поиска данных

Во всех компьютерных информационных системах поиск данных является основным видом обработки информации. При выполнении любого поиска данных имеются три составляющие, которые мы назовем атрибутами поиска:

Первый атрибут: набор данных. Это вся совокупность данных, среди которых осуществляется поиск. Элементы набора данных будем называть записями. Запись может состоять из одного или нескольких полей. Например, запись в записной книжке состоит из полей: фамилия, адрес, телефон.

Второй атрибут: ключ поиска. Это то поле записи, по значению которого происходит поиск. Например, поле ФАМИЛИЯ, если мы ищем номер телефона определенного человека.

Третий атрибут: критерий поиска, или условие поиска. Это то условие, которому должно удовлетворять значение ключа поиска в искомой записи. Например, если вы ищете телефон Сидорова, то критерий поиска заключается в совпадении фамилии Сидоров с фамилией, указанной в очередной записи в книжке.

Заметим, что ключей поиска может быть несколько, тогда и критерий поиска будет сложным, учитывающим значения сразу нескольких ключей. Например, если в справочнике имеется несколько записей с фамилией Сидоров, но у них разные имена, то составной критерий поиска будет включать два условия: ФАМИЛИЯ — Сидоров, ИМЯ — Владимир.

Как при «ручном» поиске, так и при автоматизированном важнейшей задачей является сокращение времени поиска. Оно зависит от двух обстоятельств:

1)                   как организован набор данных в информационном хранилище (в словаре, в справочнике, на дисках компьютера и пр.);

2)                   каким алгоритмом поиска пользуется человек или компьютер.

4.  Организация набора данных. Последовательный поиск

Относительно первого пункта могут быть две ситуации: либо данные никак не организованы (такую ситуацию иногда называют «кучей»), либо данные структурированы.

Под словами «данные структурированы» понимается наличие какой-то упорядоченности данных в их хранилище: в словаре, в расписании, в компьютерной базе данных.

Говоря о системах, мы выделяли важнейшее свойство всякой системы — наличие структуры. Это свойство присуще как материальным системам, так и информационным системам. Названные выше примеры хранилищ информации, а также архивы, библиотеки, каталоги, журналы успеваемости учащихся и многие другие являются системами данных с определенной структурой.

Структурированные системы данных, хранящиеся на каких-либо носителях, будем называть структурами данных.

Однако бывает и так, что хранимая информация не систематизирована. Представьте себе, что вы записывали адреса и телефоны своих знакомых в записную книжку без алфавитного индекса («лесенки» из букв по краям листов). Записи вели в порядке поступления, а не в алфавитном порядке. А теперь вам нужно найти телефон определенного человека. Что остается делать? Просматривать всю книжку подряд, пока не попадется нужная запись! Хорошо, если повезет и запись окажется в начале книжки. А если в конце? И тут вы поймете, что книжка с алфавитом гораздо удобнее.

Последовательный поиск

Ситуацию, описанную выше, назовем поиском в неструктурированном наборе. Разумный алгоритм для такого поиска остается один: последовательный перебор всех элементов множества до нахождения нужного. Конечно, можно просматривать множество в случайном порядке (методом случайного перебора), но это может оказаться еще хуже, поскольку неизбежны повторные просмотры одних и тех же элементов, что только увеличит время поиска.

Опишем алгоритм поиска методом последовательного перебора. Для описания алгоритма воспользуемся известным вам способом блок-схем (рис.

2.). В алгоритме учтем два возможных варианта результата:  1) искомые данные найдены;  2) искомые данные не найдены. 

Результаты поиска нередко оказываются отрицательными, если в наборе нет искомых данных.

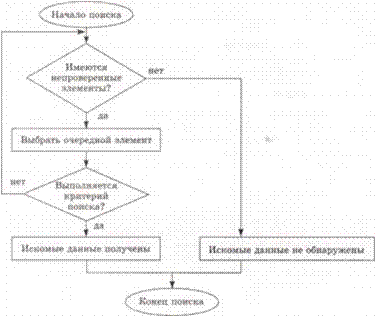
                                Рис. 2. Алгоритм поиска последовательным перебором

Символика блок-схем должна быть вам понятна. Из схемы видно, что если искомый элемент найден, то поиск может закончиться до окончания просмотра всего набора данных. Если же элемент не обнаружен, то поиск закончится только после просмотра всего набора данных.

Зададимся вопросом: какое среднее число просмотров приходится выполнять при использовании метода последовательного перебора? Есть два крайних частных случая:

•  Искомый элемент оказался первым среди просматриваемых. Тогда просмотр всего один.

•  Искомый элемент оказался последним в порядке перебора. Тогда число просмотров равно N, где N — размер набора данных. То же будет, если элемент вообще не найден.

Всякие средние величины принято определять по большому числу проведенных опытов. На этом принципе основана целая наука под названием математическая статистика. Нетрудно понять, что если число опытов (поисков) будет очень большим, то среднее число просмотров во всех этих опытах окажется приблизительно равным N/2. Эта величина определяет длительность поиска — главную характеристику процесса поиска.

Поиск половинным делением

Возьмем для примера игру в угадывание целого числа в определенном диапазоне. Например, от 1 до 128. Один играющий загадывает число, второй пытается его угадать, задавая вопросы, на которые ответом может быть «да» или «нет». Ключом поиска в этом случае является число, а критерием поиска — совпадение числа, задуманного первым игроком, с числом, называемым вторым игроком.

Если вопросы задавать такие: «Число равно единице?». Ответ: «Нет». Вопрос: «Число равно двум?» и т. д., то это будет последовательный перебор. Среднее число вопросов при многократном повторении игры с загадыванием разных чисел из данного диапазона будет равно 128/2 = 64.

Однако поиск можно осуществить гораздо быстрее, если учесть упорядоченность натурального ряда чисел, благодаря чему между числами действуют отношения больше/меньше. С подобной ситуацией мы с вами уже встречались, говоря об измерении информации. Там обсуждался способ угадывания одного значения из четырех (пример с оценками за экзамен) и одного из восьми (пример с книжными полками). Применявшийся метод поиска называется методом половинного деления. Согласно этому методу, вопросы надо задавать так, чтобы каждый ответ уменьшал число неизвестных в два раза.

Так же надо искать и одно число из 128. Первый вопрос: «Число меньше 65?» — «Да!» — «Число больше 32?» — «Нет!» и т. д. Любое число угадывается максимум за 7 вопросов. Это связано с тем, что 128 = 2⁷. Снова работает главная формула информатики.

Метод половинного деления для упорядоченного набора данных работает гораздо быстрее (в среднем), чем метод последовательного перебора.

Если максимальное число диапазона N не равно целой степени двойки, то оптимальное количество вопросов не будет постоянной величиной, а будет равно одному из двух значений: X или Х+1, где 2^х < N < 2^Х+1.

Например, если число ищется в диапазоне от 1 до 7, то его можно угадать за 2 или 3 вопроса, поскольку 2² < 7 < 2³.

Число из диапазона от 1 до 200 можно угадать за 7 или 8 вопросов, поскольку

2⁷ < 200 < 2⁸. Проверьте эти утверждения экспериментально.

Половинным делением можно искать, например, нужную страницу в толстой книге: открыть книгу посередине, понять, в какой из половин находится искомая страница. Затем открыть середину этой половины и т. д.

Набор данных может быть упорядочен не только по числовому ключу.

Другой вариант упорядочения — по алфавиту. Половинным делением можно

Половинным делением можно осуществлять поиск в орфографическом словаре или в словаре переводов слов с иностранного языка.

Блочный поиск

Снова вспомним пример с записной книжкой. Пусть в вашей записной книжке имеется алфавитный индекс в виде вырезанной «лесенки» или в виде букв вверху страницы. Несколько страниц, помеченных одной буквой, назовем блоком. Имеется блок «А», блок «Б» и т. д. до блока «Я».

Индекс — это часть ключа поиска (например,

Записи телефонов и адресов расставлялись в записной книжке по блокам в соответствии с первой буквой. Однако внутри блока записи не упорядочены в алфавитном порядке следующих букв, как это делается в словарях и энциклопедиях. Записи в книжке мы ведем в порядке поступления. При такой организации данных поиск нужного телефона будет происходить блочнопоследовательным методом:

1) с помощью алфавитного индекса выбирается блок с нужной буквой; 2) внутри блока поиск производится путем последовательного перебора. Большинство книг в начале или в конце текста содержат оглавления:

список названий разделов с указанием страниц, с которых они

начинаются. Разделы — это те же блоки. Поиск нужной информации в книге начинается с просмотра оглавления, с дальнейшим переходом к нужному разделу, который затем просматривается последовательно. Очевидно, это тот же блочно-последовательный метод поиска.

Списки с указанием на блоки данных называются списками указателей.

Разбиение данных на блоки может быть многоуровневым. В толстых словарях блок на букву «А» разбивается, например, на блоки по второй букве: блок от «АБ» до «АЖ», следующий от «A3» до «АН» и т. д. Такой порядок называется лексикографическим.

В поисковом множестве с многоуровневой блочной структурой происходит поиск методом спуска: сначала отыскивается нужный блок первого уровня, затем второго и т. д. Внутри блока последнего уровня может происходить либо последовательный поиск (если данных в нем относительно немного), либо оптимизированный поиск типа половинного деления. Поиску методом спуска часто помогают многоуровневые списки указателей.

Поиск в иерархической структуре данных

Многоуровневые блочные структуры хранения данных называются иерархическими структурами. По такому принципу организовано хранение файлов в файловой системе компьютера. То, что мы называли выше блоками, в файловой системе называется каталогами или папками, а графическое изображение структуры блоков-папок называется деревом каталогов. Пример отображения на экране компьютера дерева каталогов.

Чтобы найти файл, нужно знать путь к файлу по дереву каталогов. Операционная система поможет найти запрашиваемый вами файл по команде Поиск. Результат поиска представляется в виде пути к файлу, начиная от корневого каталога последовательно по уровням дерева до каталога (папки), непосредственно содержащего ваш файл. Например, при поиске файла с именем ke.exe будет выдан следующий ответ:

Е: \GAME\GAMES\ARCON\ke. ехе

Здесь указан полный путь к файлу на логическом диске Е: от корневого каталога до самого файла. Имея такую подсказку, вы легко отыщете нужный файл на диске методом спуска по дереву каталогов. Каталог иерархической структуры файловой системы компьютера является многоуровневым списком указателей.

Домашнее задание:

1.     Проработайте лекционный материал.

2.     Составьте конспект.

3.     Выполните задания и ответьте на вопросы.

1)       Что относится к атрибутам поиска?

2)       Приведите примеры неорганизованных и структурированных множеств поиска, помимо тех, что даны в тексте параграфа.

3)       В журнале успеваемости учащихся со сведениями о годовых оценках требуется осуществить поиск всех отличников по информатике. Что в этой ситуации является набором данных, что — ключом поиска, что — критерием поиска?

4)       Попробуйте внести изменение в блок-схему на рис. 1 так, чтобы алгоритм учитывал возможность выбора нескольких элементов набора данных, удовлетворяющих одному и тому же значению критерия поиска. Например, позволял решить задачу поиска из задания 3.

5)       Что такое список указателей? Посмотрите свои учебники по разным предметам. Определите, какие списки указателей там использованы: простые или многоуровневые?