Линии первого и второго порядка текст к презентации презентация по математике

Линии первого и второго порядка

Впервые линии второго порядка изучались Менехмом, учеником Евдокса. Его работа заключалась в следующем: если взять две пересекающиеся прямые и вращать их вокруг биссектрисы образованного ими угла, то получится конусная поверхность. Если же пересечь эту поверхность плоскостью, то в сечении получаются различные геометрические фигуры, а именно эллипс, окружность, парабола, гипербола и несколько вырожденных фигур.

Линии первого порядка

К линиям первого порядка относятся те линии, для которых задающее их уравнение содержит переменные X и у только в первой степени. Иными словами, такие линии описываются уравнениями вида

Где А, В и С — постоянные числа. Из этого уравнения можно выразить переменную У как функцию от аргумента Х При В ≠ 0

Данное Уравнение называют Уравнением прямой с угловым коэффициентом K = tg φ, где φ — угол наклона прямой к положительному направлению оси Ох. Если K = 0, то прямая параллельна оси Ох и отстоит от нее на B масштабных единиц.

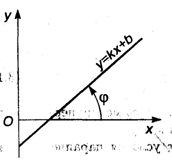
Кроме "классического" уравнения прямой следует знать еще две его разновидности. Первая из них — это уравнение прямой с заданным угловым коэффициентом K, проходящей через заданную точку (X0, У0):

Другой вид — это уравнение прямой, проходящей через две заданные точки на плоскости (X1, Y1) и (х2, у2):

Угол между прямыми. Рассмотрим две прямые, заданные уравнениями У = K₁X + B₁ и У = K₂X + B₂, где K₁ = tg φ1 и K₂ = tg φ2. Пусть φ — угол между этими прямыми. Тогда φ = φ2 — φ1 и мы получаем:

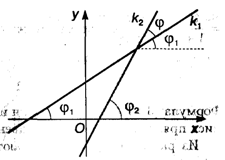
Из данной формулы вытекают условия параллельности и перпендикулярности прямых:

·         Если прямые параллельны, то

·         Если прямые перпендикулярны, то

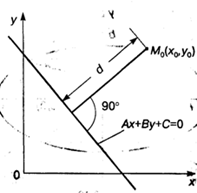
Расстояние от точки до прямой. Пусть прямая задана уравнением общего вида. Тогда расстояние D от произвольной точки М0(X0, Y0) до прямой задается формулой

Линии второго порядка

Линии второго порядка, плоские линии, декартовы прямоугольные координаты которых удовлетворяют алгебраическому уравнению 2-й степени:

a₁₁x² + a₁₂xy + a₂₂y² + 2a₁₃x + 2a₂₃y + a₁₁ = 0

Три наиболее используемых вида линий: эллипс, гиперболу и параболу.

1.      Эллипс.

Линия, для всех точек которой сумма расстояний от двух данных точек, называемых фокусами, есть величина постоянная и большая, чем расстояние между фокусами, называется Эллипсом. Согласно определению эллипса, сумма расстояний от произвольной точки М на этой линии до его фокусов F1 и F2 постоянна: Точки F1и F2 называются фокусами эллипса векторы F1M и F2M− фокальными радиус-векторами, а числа r1=|F1M| и r2=|F2M|− фокальными радиусами точки M, принадлежащей эллипсу.

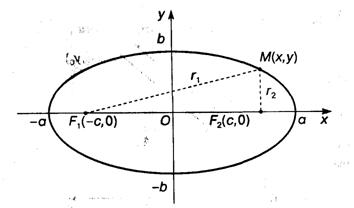
Отсюда можно вывести уравнение эллипса в его основной форме:

Где А и B — полуоси эллипса. Из уравнения следует, что оси эллипса являются его осями симметрии, а точка их пересечения — центром его симметрии.

Прямые, перпендикулярные главной оси и проходящей на расстоянии a/e от центра, называются директрисами эллипса. (где e=c/a=√1−b²/a² (0≤e<1) называется эксцентриситетом эллипса)

Теорема. (Директориальное свойство эллипса) Эллипс является множеством точек, отношение расстояний от которых до фокуса и до соответствующей директрисы постоянно и равно e.

2.      Гипербола.

Гиперболой называется линия, для всех точек которой модуль разности расстояний от двух данных точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.

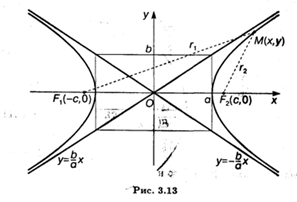
На рисунке показаны все основные элементы гиперболы. Разность расстояний от произвольной точки М на гиперболе до фокусов F1 и F2, согласно определению, есть величина постоянная:

Из этого выводится основное уравнение гиперболы, которое имеет вид:

Характеристикой эллипса, показывающей меру его вытянутости, является Эксцентриситет — величина, определяемая отношением

Где С- фокус эллипса

3.      Парабола.

Параболой называется линия, все точки ко­торой находятся на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой дирек­трисой и не проходящей через фокус.

Согласно определению, точка М(х, у) лежит на параболе, если R1 = R2. Отсюда и выводится уравнение параболы, которое имеет вид:

График параболы показан на рисунке.

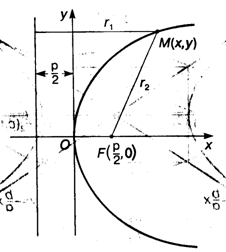
Нетрудно видеть, что перемена осей координат приводит к более привычному уравнению параболы вида У = Ах2, где А — постоянное число.

Исследование вида линий второго порядка может быть проведено без приведения общего уравнения к нужному виду. Это достигается совместным рассмотрением значений т. н. основных инвариантов линии второго порядка — выражений, составленных из коэффициентов уравнения 2-й степени, значения которых не меняются при параллельном переносе и повороте системы координат:

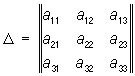
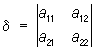
S = a₁₁ + a₂₂, (a_ij = a_ji).

Пример. 1

Найти угол между прямыми, заданными уравнениями У = 2X - 5 и У = -3X + 4.

Решение.

Подставляя в формулу значения K1 = 2 и K2 = -3, имеем

Откуда получаем, что один из углов равен φ =

Пример. 2

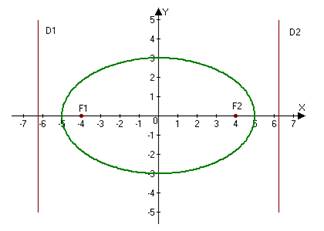
Построить эллипс 9x²+25y²=225. Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения директрис.

Решение.

  Приведем уравнение эллипса к основному виду:

9x²+25y²=225|:225

Находим полуоси a=5, b=3.

Фокусы найдем по формулам: F1(−c,0)  и F2(c,0), где c=

c===4=> F1(−4,0), F2(4,0)

Эксцентриситет

Уравнения директрис находим по формулам  и

Сделаем рисунок