Математика_7класс_Расположение высот треугольника_Приложение 3

В отличие от медианы или биссектрисы, высота треугольника может быть расположена как внутри треугольника, так и вне его.

Определение.

Высотой треугольника называется (1)______________, проведенный из вершины треугольника к прямой, содержащей противолежащую сторону.

 На рисунке выше: (2) _____ — высота, проведенная из вершины B к стороне AC.

Все три высоты треугольника пересекаются в одной точке. Эта точка называется (3)________________треугольника.

Высоты остроугольного треугольника расположены строго (4) ___________ треугольника.

Соответственно, точка пересечения высот также находится (5)___________ треугольника.

В прямоугольном треугольнике две высоты совпадают со (6)_____________. (Это высоты, проведенные из вершин острых углов к катетам).

Высота, проведенная к (7)_______________, лежит внутри треугольника.

(8)____ — высота, проведенная из вершины С к стороне AB.

AB — высота, проведенная из вершины B к стороне (9) _____.

(10)____ — , проведенная из вершины прямого угла А к гипотенузе ВС.

Высоты прямоугольного треугольника пересекаются (11)_________________________________ ((12)_____ — ортоцентр).

В (13) _________________треугольника внутри треугольника лежит только одна высота — та, которая проведена из вершины (14)___________ угла.

Две другие высоты лежат (15)_______ треугольника и опущены к (16)_____________ сторон треугольника.

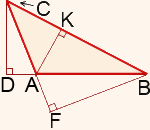
AK — высота, проведенная к стороне (17)____.

(18)____ — высота, проведенная к продолжению стороны АС.

CD — (19)___________, проведенная к продолжению стороны AB.

Точка пересечения высот тупоугольного треугольника также находится (20)_______треугольника:

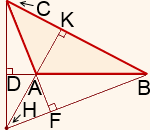
(21)____ — ортоцентр треугольника ABC.

Скачано с www.znanio.ru