Математика_7класс_Вписанная и описанная окружности_дополнительный материал 1

Приложение 4

Теоретический материал

Окружность, описанная около треугольника

Окружность называется описанной около треугольника, если она проходит через все его вершины.

   Теорема о центре окружности, описанной около треугольника.

     Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к сторонам треугольника, проведенных через середины этих сторон.

Дано: АВС - данный треугольник; О - центр описанной около него окружности (рис 30.).

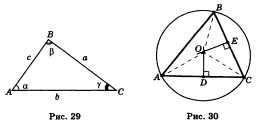
Доказать: О - точка пересечения серединных перпендикуляров.

     Доказательство. Треугольник АОС равнобедренный: у него стороны О А и ОС равны как радиусы. Медиана OD этого треугольника одновременно является его высотой. Поэтому центр окружности лежит на прямой, перпендикулярной стороне АС и проходящей через ее середину. Точно так же доказывается, что центр окружности лежит на перпендикулярах к двум другим сторонам треугольника.

     Замечание. Прямую, проходящую через середину отрезка перпендикулярно к нему, часто называют серединным перпендикуляром. В связи с этим иногда говорят, что центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам треугольника.

   Теорема об окружности, описанной около треугольника.

     Около любого треугольника можно описать окружность.

     Дано: АВС - данный треугольник; О - точка пересечения серединных перпендикуляров (рис 31.).

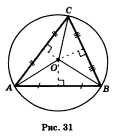
Доказать: О - центр окружности, вписанной в АВС.

Доказательство. Обозначим буквой О точку пересечения серединных перпендикуляров к его сторонам и проведем отрезки ОА, ОВ и ОС. Так как точка О равноудалена от вершин треугольника АВС, то ОА = ОВ = ОС Поэтому окружность с центром О радиуса ОА проходит через все три вершины треугольника и, значит, является описанной около треугольника ABC.

     Замечание. Отметим, что около треугольника можно описать только одну окружность. В самом деле, допустим, что около треугольника можно описать две окружности. Тогда центр каждой окружности равноудален от вершин треугольника и, значит, совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают. Окружность, вписанная в треугольник

Окружность, вписанная в треугольник.

Окружность называется вписанной в треугольник, если она касается всех его сторон.  

Теорема о центре окружности, вписанной в треугольник.   

     Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.

     Дано: АВС — данный треугольник; О — центр вписанной в него окружности; D, Е и F — точки касания окружности со сторонами треугольника (рис. 27).

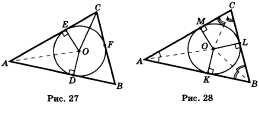
    Доказать: О — точка пересечения биссектрис.   

     Доказательство. Прямоугольные треугольники AOD иАОЕ равны по гипотенузе и катету. У них гипотенуза ОА — общая, а катеты OD и ОЕ равны как радиусы. Из равенства треугольников следует равенство углов OAD и ОАЕ. А это значит, что точка О лежит на биссектрисе треугольника, проведенной из вершины А. Точно так же доказывается, что точка О лежит на двух биссектрисах треугольника.   

   Теорема об окружности, вписанной в треугольник.   

     В любой треугольник можно вписать окружность.   

     Дано: A ABC — данный треугольник, О — точка пересечения биссектрис, М, L и К — точки касания окружности со сторонами треугольника (рис. 28).   

     Доказать: О — центр окружности, вписанной в АВС.   

     Доказательство. Проведем из точки О перпендикуляры OK, OL и ОМ соответственно к сторонам АВ, ВС и СА (см. рис. 28). Так как точка О равноудалена от сторон треугольника ABC, то О К = OL = ОМ. Поэтому окружность с центром О радиуса ОК проходит через точки K L M. Стороны треугольника ABC касаются этой окружности в точках К, L, М, так как они перпендикулярны к радиусам ОК, OL и ОМ. Значит, окружность с центром О радиуса ОК является вписанной в треугольник ABC. Теорема доказана.   

     Замечание. Отметим, что в треугольник можно вписать только одну окружность. В самом деле, допустим, что в треугольник можно вписать две окружности. Тогда центр каждой окружности равноудален от сторон треугольника и, значит, совпадает с точкой О пересечения биссектрис треугольника, а радиус равен расстоянию от точки О до сторон треугольника. Следовательно, эти окружности совпадают.