
Тема урока: «Дроби и длительности нот»
Цели урока:
• закрепление знаний учащихся об обыкновенных дробях (приведение к общему знаменателю, сравнение дробей);
• обобщение понятия о дробях на основе их распространения на ситуации с нотами;
• закрепление видения нот как своеобразной (без цифровой) знаковой формы дробей;
• расширение кругозора учащихся;
• воспитание интереса и уважения к изучаемому предмету.
Оборудование: пианино; опорная схема «Дроби и ноты»; раздаточные карточки (по числу учащихся); задания для учащихся, оформленные в виде плакатов.
1. Оргмомент.
Психотеропия
- Сели поудобнее, начинаем наблюдать за нашим дыханием.
- Сосредотачиваем внимание на груди и настраиваемся на восприятие самых светлых и радостных сторон жизни.
- Почувствовали тёплое и дружеское расположение к себе и к окружающему миру.
- Начинаем вспоминать самые светлые и радостные стороны жизни, когда солнце успеха, удачи и победы освещали ваше лицо радостью.
- Весёлый огонёк загорается в вашей груди.
- Прекрасная музыка идёт в такт, и в унисон вашим радостным переживаниям.
- Вам хочется обнять весь мир и простереть в восторге от него свои " руки- крылья".
- Вытянули правую руку, почувствовали тепло. Протянули левую руку, чувствуем тепло.
- На левую руку сели нотки, на левую - дроби.
- Плавно соединяем руки, т.е. ноты и дроби.
II. Объяснение материала новой темы
Мы живем в мире звуков. Люди давно научились записывать различные звуки с помощью специальных знаков. Звуки человеческой речи, например, записываются с помощью букв, а музыкальные звуки записываются € помощью нот.
Ноты отличаются по длительности их звучания. Самая «длинная» нота - целая. Ее обозначают знаком 0. С точки зрения математики целую ноту можно принять за единицу. Давайте послушаем, как долго звучит эта нота.
(Ассистент учителя демонстрирует длительность звучания целой ноты со счетом вслух: «1-и-2-и-3~и-4-и».)
Запишем:
- целая (1).
Нота вдвое короче называется половинной. Послушаем длительность звучания половинной ноты…
Какая же дробь соответствует половинной ноте? Половинной
ноте соответствует дробь ![]()
Запишем:
- половинная (![]() )
)
Послушаем ноту, которая еще в два раза короче ...
Это четвертая.
Запишем:
-четвертая (![]() )
)
Восьмая нота имеет еще меньшую длительность. Слушаем...
- восьмая (![]() )
)
И, наконец, самая короткая нота - шестнадцатая...
- шестнадцатая (![]() )
)
III. Закрепление
(На доске появляется опорная схема.)
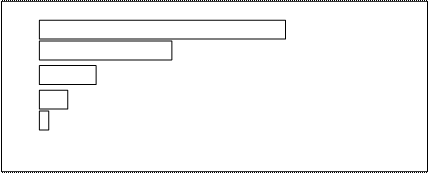 |
Вопрос: Какая же нота имеет наименьшую длительность? наибольшую?
Сравним длительности звучания таких нот (плакат на доске):
 |
1.(![]() >
>![]() )
=> (
)
)
=> (
)
Надо ли приводить эти дроби к общему знаменателю? Нет, не надо, так как у них одинаковые числители, а из двух дробей с равными числителями больше та, у которой знаменатель меньше.
2. (![]() <1)
=> ( )
<1)
=> ( )
3. ( ![]() <
<![]() ) => ( )
) => ( )
4. ( ![]() +
+![]() =
=![]() =
=![]() ) => ( )
) => ( )
Но в музыке не используется знак «+», поэтому равенства длительностей нот лучше записывать так:
 |
Проверим эти равенства:
а)
, так как ![]() +
+![]() +
+![]() =
= ![]() =
=![]() =1
=1
б)
, так как ![]() +
+![]() +
+![]() =
=![]() =
=![]() =
=![]()
![]()
Задание 1. В приведенных равенствах одной ноты не хватает:
Найдите недостающую ноту.
Решение. 1) ![]() +
+![]() =
=![]() +
+![]() +
+![]() +х
+х
х=![]() => ( )
=> ( )
2) ![]() +
+![]() =
=![]() +
+![]() +
+![]() +
+![]() +у
+у
у=![]() =>
( )
=>
( )
- Посмотрим теперь на нотный стан, изображенный на доске и на раздаточных, карточках:
Из рисунка мы видим, что нотная запись разбита вертикальными линиями на отдельные части. Каждая такая часть называется тактом.
Задание 2. Подсчитаем общую длительность всех нот, входящих в каждый такт (все ответы запишем в виде дроби со знаменателем 4):
![]() +
+![]() +
+![]() +
+![]() =
=![]() =
=![]()
![]() +
+![]() +
+![]() =
=![]() +
+![]() =
=![]() +
+![]() =
=![]()
![]() +
+![]() =
=![]()
![]() +
+![]() +
+![]() +
+![]() =
=![]()
![]() +
+![]() +
+![]() +
+![]() =
=![]()
Как видим, в каждом случае мы получили одно и тоже число - число
![]() . Это число называется размером
музыкального произведения и записывается в начале нотного стана.
. Это число называется размером
музыкального произведения и записывается в начале нотного стана.
(Записываем.)
Теперь послушаем то произведение, с нотной записью которого мы работали. Угадайте название этой песни.
(Русская народная песня «Во поле береза стояла».)
'Задание 3 (на карточках). На карточке записана мелодия без разбиения на такты. Сделайте самостоятельно, зная размер произведения.
Вспомогательные записи (или устные вычисления):
Результат:
Послушаем эту мелодию и угадаем название песни.
( "Снегопад", "Крылатые качели".)
Задание 4. Запишите дроби:
![]() ,
, ![]() ,
,
![]() ,
, ![]()
Назовите общие признаки этих чисел.
1. Все эти числа являются обыкновенными дробями.
2. Числители всех дробей равны 1.
3. Знаменатели являются четными числами.
4. Эти дроби соответствуют длительности звучания разных нот.
Вопросы:
Какая из этих дробей наибольшая? Наименьшая?
В каком порядке расположены эти дроби?
(В порядке убывания.)
IV. Подведение итогов урока.
Литература
1. НЯ. Виленкин, А.С. Чесноков и др. Математика. Учебник для 6 класса средней школы. - М., Просвещение, 1993. - С. 153, №926.
2. НД. Изместьсва, НЛ. Терский. Учитель - конструктор познавательного процесса.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.