
Қазақстан Республикасының Білім және ғылым министрлігі
Түркістан облысы
Отырар ауданды
Ө.Жәнібеков атындағы №4 жалпы орта лицей-интернаты
Математикалық сауаттылыққа берілген есептердің шешу жолдары және олардың өмірде, тұрмыста қолдануы.
Жұмыстың авторы: Рысбайқызы Жанна
Сыныбы: 9
Жұмыстың секциясы: Қолданбалы математика
Жетекшісі: математика пәнінің мұғалімі
Мылтыкбаева Арайлым Абилкасымовна
Шәуілдір – 2019-2020 жыл
Мазмұны:
І. Жұмыстың сипаттамасы.............................................................................1-2
ІІ. Кіріспе.........................................................................................................3-4
Теңдеу
ІІІ. Зерттеу бөлімі: Математикалық сауаттылыққа берілген есептің қолданулары.....................................................................................................5-13
1) Есептерді шығару алгоритмі
2) «Теңдеулер шешу» тақырыбына ұсынылатын есептер
3) Шырылдауық шегіртке
4) Ойын-сауық кешінде
5) «Қисынсыз жору»
6) Теңдеу біз үшін ойлайды.
7) Үш таңбалы сан
8) Шаштаразда
9) Трамвай мен жаяу адам
10) Пароход пен сал
11) Теңіздегі барлау
12) Велодромда
IV. Қорытынды………………………………………………………………14
V. Оқушы күнделігі.........................................................................................15
VІ. Қолданылған әдебиеттер………………………………………………...16
Ғылыми жұмыстың мақсаты: : Математикалық сауаттылықта берілген теңдеулердің өмірмен байланысын сезіну, оларды шығару, толық баяндау, шешу әдістерін қарастыру және мысалдармен бекіту.
Ғылыми жұмыстың міндеттері:
1. математикалық теңдеулер түсінігін ашып көрсету;
2. математикалық теңдеулерді дәлелдеу;
3. математикалық теңдеулерді шешу әдістерін қарастыру;
4. теңдеулердің математикадағы орнын танып білу. Сондықтан да, әрбір оқушы математикалық сауатты болу үшін мынадай мақсаттар жүзеге асырылу керек.
5. Ақыл-ойды дамыту.
6. Математикалық іс-әрекеттің сипатына сай ойлауды қалыптастыру.
7. Қоғамдық өмір практикасына қажетті математикалық ойлауды қалыптастыру.
8. Математикалық білімді игеру мақсатында практикада қолдану.
9. Болмысты, табиғат пен қоғамды тануға қажет математикалық мазмұндай білу.
10. Алдына қойылған сұрауға немесе есепті шығаруға оптимальды (жылдам, сенімді және дұрыс) жауап беруге дағдылану, ұмтылу.
11. Осы мақсатты ескере отырып, математикаға қызығушылығымды арттыру барысында ойлау қабілетімді дамыту үшін әртүрлі теңдеуге қатысты есептерді шешуді жүзеге асыруды жөн көрдім. Теңдеулер математикалық олимпиадаларда, әр түрлі жарыстарда жиі қолданылады, және өмірмен тығыз айланысты.
Жұмыстың өзектілігі
Халыққа білім беру жүйесінің барлық буындарына соның ішінде бастауыш және орта буынға, зор жауапкершілік жүктейді. Өйткені білім мен тәлім тәрбиенің негізі бастауыш мектепте қаланады.
Қандай да болсын пәнді, соның ішінде бастауыш және орта мектептегі математиканы, оқытып-үйрету арнайы мақсат көздейді.
Қазіргі жағдайда математикалық біліммен, әсіресе теңдеу ұғымымен және оның өзіндік әдіс-тәсілдерімен, арнайы тілімен қарулану қоғам мүшелерінің қай саласына болса да аса қажетті.
Оқу пәні ретінде математика курсы оқушылардың белгілі бір білім көлемін игеруін көздейді.
Математикалық теңдеулер нақты түрде ұсынылмайды тікелей оқушыны қоршаған ортамен байланыстырады, демек олардың танымдық қызығушылығын тудырады, ғылыми көзқарасын қалыптастырады.
Жұмыстың ғылыми жаңалығы
Қазіргі таңда жылма жыл есептердің күрделенуі, есептерді шығарудың әр түрлі әдістері, жаңаша есептердің енуі, өмірлік заңдылықтардан туындаған мәселелерді теңдеулер құру арқылы шығару өте маңызды. Теңдеу бұл тылсым дүниенің жұмбағын шеше білу іспетті.
Зерттеу әдісі
Бұл жұмысты жазу барысында ғылыми әдебиеттермен жұмыс, жинақтау, жүйелеу, түсіндірмелі әдістер, есептер шығару, зерттеулер қолданылады.
Кіріспе
Кез келген мемлекеттің болашағы – бүгінгі жас ұрпақ екені белгілі қағида. Дамыған 50 – елдің қатарына енуге мүмкіндік беретін құдіретті күш – білім.
Математика
сөзінің өзі грек тілінде білім, ғылым деген
мағынаны білдіреді. Олай болса ежелгі замандардан - ақ
математикалық білімді ғылымның жоғары дәрежесі
ретінде қабылдаған.
Математика – ғылым болмысынан балама ұғымдар. Сондықтан
да математика барлық ғылымдардың логикалық негізі –
күре тамыры ретінде қарастырылады.
Мектеп математика курсында теңдеу тақырыбы - елеулі орын алар
математиканың ерекше бөлімі деуге болады. Адамдар бір
шаруаның шешімін таппағанда, түсініксіз
тығырыққа тірелгенде, бұл бір ЖҰМБАҚ
НӘРСЕ екен деп айтып жатады. Ал математиканың жұмбағы –ТЕҢДЕУЛЕР.
Теңдеулерді шешуді ойға қонымсыз абстракциялы ұғым деп түсінбеймін, керісінше, оны кез келген оқиғаның ақиқат не жалған екендігіне көз жеткізу деп білемін. Егер адам шындыққа құмар жан болса, онда өмірдің қойған сансыз сауалдарына жауап беруге тырысады деген ойдамын. Теңдеулер тек математикада емес, сонымен қатар теңдеулер – өмірдің сан алуан белгісіз, құпия, сыры ашылмаған, әлі беймәлім, тығырықтан шығар жолды іздеумен, тек ізденумен жұмыс жасауды қажет етеді. Міне, қазіргі таңда математика саласында математикалық сауаттылық ұғымы математиканы өмірде қалай қолдануға болатындығын көрсету үшін енгізілген. Адам математикадан сауатты болмай өмірде алға қойған мақсаттарына жетуде жеңіліске ұшырауы мүмкін. Кез келген істе математикадан сауатты болған жағдайда жеңіліс таппайды, ұтылмайды. Адам қанша мөлшерде шыған шығарамын, қанша мөлшерде пайда табамын, оның денсаулығыма қанша мөлшерде зияны не пайдасы болады – деген сан қилы сұрақтардың шешімі математикаға тығыз байланысты. Оның жауабы білмегенге жұмбақ, білгенге дұрыс теңдеу құрып, жауабын, шешімін табу.
Белгісіз элемент есеп шығару арқылы немесе байқап көру, іздену үрдісімен жүреді. Ойша болжай білу, тапқырлық пен аңғарымпаздықты байқатады. Аңғарымпаздық өз білімін пайдалана білудің көрсеткіші.
Теңдеу дегеніміз құрамында мәнін табу керек болатын әрпі бар теңдік. Теңдеуді шешу дегеніміз оның барлық түбірлерін табу немесе оның бірден-бір түбірі болмайтынына көз жеткізу. Теңдеуді тура санды теңдікке айналдыратын әріптің мәні теңдедің түбірі деп аталады.
· Мысалы, 7x+5=26 -теңдеу
· x=3
· 3- саны теңдеудің түбірі

Франсуа Виет(1540-1603)-атақты француз математигі.Виет белгісіз сандардың орнына әріптерді пайдалануды ұсынған.

Рене Декарт(1596-1650)-атақты француз математигі.Ол белгісіз санды немесе шаманы х,у,z әріптерімен белгілеуді ұсынған(1637).
Теңдеуді теңдеудегі белгісіздері бар қосылғыштарды теңдеудің бір жағына, белгісіздері жоқ қосылғыштарды екінші жағына көшіру арқылы шешуге болады. Ол үшін:
1) Барлық айырымдарды қосынды түрінде жазу керек;
2) Сәйкес қосылғыштарды қарама-қарсы таңбамен теңдеудің екінші жағына көшіру керек.
Негізгі бөлім
3.1. Теңдеу құру арқылы шығарылатын есептерді шығару алгоритмі:
Есептің құруға берілген есептерін шығару үшін;
1. Белгісіз шамаларды анықтау.
1. Теңдеу құру;
1. Теңдеуді шешу;
1. Теңдеудің шешімдерін зерттеу.
1. Есепті тексеру;
1. Есептің толық жауабын жазу, шарттарын орындау қажет.
3.2. «Теңдеулер шешу» тақырыбына ұсынылатын есептер:
«Барлығы қанша қарға?»
Келеді ұшып екі қарға,
Топ достарын ертіп талға
Болды елу әлгі жиын
Санағанда демей қиын.
Болмаңыздар әбігер,
Шешімі табылар бәрі бір.
Айтпай есеп шарты кім,
Теңдеу құру тәртібін?
Жауабы: 2+х=50, х=48 қарға
«Кетті бірге нешеуі»
Кездесіп бір топ аңменен,
Болды 30 бас малменен.
Олар кетті қоштасып,
Үш түлкімен достасып.
Теңдеуді ойлап құрыңыз,
Мал санын айта тұрыңыз.
Жауабы: х+3=30, х=27 бас мал.
3.4. Ойын-сауық кешінде
«Ойдағы санды табу өнері»
Фокусшы әдетте мынадай іспетті әрекет жасауды ұсынады; бір сан ойла, 2-ні қос, 3-ке көбейт, 5-ті азайт, ойлаған санды азайт т. с. .с.-барлығы бес, кейде ондаған амал орындатады. Сонан соң фокусшы сенде шыққан нәтижені сұрап біледі де, сол сәтте сен ойлаған санды атайды.
«Фокустың» сыры, әрине, ап-айқын, оның негізіне теңдеулер алынған.
Мысалы, фокусшы саған төмендегі таблицаны сол жақ бағанындағы амалдар алгоритмін орындауды ұсынған болсын дейік:
Сонан соң фокусшы сенен ең соңғы шыққан нәтижені айтуды өтінеді, оны сен айтқан соң, сол сәтте ойланған санды атайды. Ол мұны қалай тапты?
Мұны түсіну үшін таблицаның оң жағындағы бағанға қараңдар, онда фокусшының нұсқаулары алгебра тіліне аударылған.
Осы бағаннан, егер сен қандай да бір х санын ойлаған болсаң онда барлық амалдарды орындаған соң сенің жауабыңда 4х+1 шығуы керек. Осыны біле отырып, ойланған санды «табу» қиын емес.
Мысалы, сен фокусшыға 33 шыққанын айттың дейік. Сол кезде фокусшы ойша 4х+1 = 33 теңдеуін тез шешеді де, х = 8 екенін табады. Екінші сөзбен айтқаңда, соңғы шыққан нәтижеден 1-ді шегеріп (33 — 1 = 32), шыққан санды 4-ке бөлу керек (32:4 = 8), бұл ойланған сан (8) болып табылады.Егер де сенде 25 шыққан болса, онда фокусшы ойша 25—1=24, 24:4 = 6 амалдарын. орындайды да, сенің-6-ны ойлағаныңды айтады.
Сендер осыларды түсініп алып, таныстарыңды бұрынғыдан бетер таңырқатып әрі қайран қалдыруларыңа болады, бұл үшін оларға, әлгі ойланған санға өздерінің қалаған амалдарын, қолдануды ұсыныңдар. Сен танысыңа бір сан ойлауды және оған белгілі бір санды қосу немесе азайту (айталық: 2-ні қосу, 5-ті азайту т. с. с), белгілі бір санға (2-ге, 3-ке т. с с) көбейту, ойланған санды қосу немесе сол санға азайту амалдарын кез келген ретпен орындауды ұсынасың. Танысың сені шатастыру үшін амалдарды ұзарта түседі. Мысалы, ол 5 санын ойға ұстап (бұл санды сізге айтпайды) және амалдарды ойша орындай отырып, былай дейді:
— Мен бір сан ойладым, оны 2-ге көбейттім, нәтижеге 3-ті қостым, сонан соң ойланған санды қостым; мен енді 1-ді қостым, 2-ге көбейттім, ойланған санға азайттым, 3-ке азайттым тағы да ойланған санды азайттым, 2-ге азайттым. Мен ең соңында нәтижені 2-ге көбейттім және 3-ті қостым.
Сені осылайша әбден шатастырдым деп біліп, ол масаттанған түрмен саған:
— 49 шықты дейді.
Сен оны таңырқатып дереу оның ойға 5 санын жасырғанын айтасың.
Сен мұны қалай таптың? Енді бұл ете айқын. Танысың саған өзі ойлаған санға қолданатын амалдарын айтқан кезде, сен онымен бір мезгілде ойша х белгісізіне амал қолдан. Ол саған «Мен бір сан ойладым» дегенде, сен өзіңше «демек, х саны» деп біл. Ол: «... оны 2-ге көбейттім...» дегенге (ол шынында өзі ойлаған санын көбейтеді), сен өзіңше: «енді 2х» болды деп жалғастыр. Ол: «...нәтижеге 3-ті қостым...» дегенде, сен бірден 2х+3 болды деп жалғастыр т.с.с. Ол сені әбден «шатастырып», жоғарыда айтылған амалдардың бәрін орындап болған соң, мына таблицада көрсетілгендей жайт шықса (мұның сол жақ бағанында сенің танысың естіртіп айтатын амалдары, ал оң жақтағысында сенің ойша орындайтын амалдарың жазылған):
|
Мен бір сан ойладым, |
х |
|
оны 2-ге көбейттім, |
2х |
|
нәтижеге 3-ті костым, |
2х+3 |
|
мұнан соң ойланған санды костым, |
3х+3 |
|
мен енді 1-ді қостым, |
3х+4 |
|
2-ге көбейттім, |
6х + 8 |
|
ойланған санға азайттым, |
5х+8 |
|
3-ке азайттым, |
5х+5 |
|
тағы да ойланған санды азайттым, |
4х + 5 |
|
2-ге азайттым, |
4х+3 |
|
мен сен соңында нәтижені 2-ге көбейттім |
8х+ 6 |
|
және 3-ті қостым |
8х+9 |
Сен ең ақырында ең соңғы нәтиженің 8х+9 екенін ойыңа ұстайсың. Енді ол: «49 шықты» дейді. Ал сенің ойыңда теңдеу дайын тұр: 8х + 9 = 49. Мұны шешу саған оп оңай, сен бірден оның 5 санын ойлағанын айтасың.
Бұл фокустың ерекше күшті әсер ету себебі, ойланған санға қолданылатын амалдарды сен емес, оларды сенің жолдасыңның өзінің «ойлап табуында».
Фокус іске аспайтын бір жағдай бар. Мысалы: егер бірнеше амал қолданылғаннан кейін өзіңде (ойша іштен есептегенде) х+14 теңдеуі шығып, ал жолдасың: «...мен енді ойлаған санға кеміттім, сонда 14 шықты» десе, онда өзің (х+14)— х=14 болатынын байқай отырып, шынында 14 шығатынын аңғарасың, ешқандай теңдеу шықпағандықтан өзің ойланған санды анықтай алмайсың. Мұндай жағдайда не істеу керек Былай істеңдер: ойша есептеуіңде х белгісізі болмайтын нәтиже шыққанда, жолдасыңа: «Тоқтай қал! Мен енді ештеңе сұрамай-ақ сенің есептеуіңде 14 саны шыққанын айта алам»— деп, сөзін бөл. Бұл жайт танысыңды әбден таңырқатады — себебі ол өзіңе ештеңе айтқан жоқ емес пе!
Сен ойлаған санды біле алмағаныңмен, фокус өте әсерлі болып шығады!
Мысал келтірейік (бұрынғыша сол жақ бағанда танысыңның айтқандары жазылған):
|
Мен бір сан ойладым, |
х |
|
|
|
|
оған 2-ні қостым, |
х+2 |
|
нәтижені 2-ге көбейттім, |
2х+4 |
|
мен енді 3-ті қостым, |
2х + 1 |
|
ойланған санға азайттым, |
х+7 |
|
5-ті қостым, |
х+12 |
|
мен енді ойланған санға азайттым |
12 |
Осы сәтте, сенде 12 саны, яғни х белгісізі жоқ өрнек шыққан кезде, сен жолдасыңның сөзін бөліп, оның есептеуінде 12 санының шыққандығын айтасың.
Біраз жаттығып алып, танысыңа осындай «фокусты» оп-оңай керсете алатын боласың.
3.5. ЕСЕ П . «Қисынсыз жору»
Мынау бір есеп мүлде мағынасыз болып көрінуі мүмкін:
Егер 8•8 = 54 болса, 84 неге тең?
Осы оғаш сұрақ онша мағынасыз емес, бұл есепті теңдеу құрып шығаруға болады.
ШЕШУІ: Бәлкім, сендер есепке енген сандардың ондық санау системасында жазылмағандығын аңғарған боларсыңдар — әйтпесе «84 неге тең» деген сұрақ мағынасыз болған болар еді. Белгісіз санау системасының негізі х болсын. «84» саны бұл жағдайда екінші разрядтың 8 бірлігін және бірінші разрядтың 4 бірлігін көрсетеді, яғни
84 = 8х + 4.
«54» саны 5х + 4 екенін көрсетеді. 8•8 = 5х + 4 теңдеуі шығады, бұл ондық санау системасында
64 = 5х+ 4 болып жазылады, бұдан х=12. Сан он екілік санау системасында жазылған,
«84» == 8•12+4=100. Сонымен, егер 8•8=«54» болса, онда
«84» = 100.
Мына түрдегі есепте осыған ұқсас шығарылады: 5•6 = 33 болганда, 100 неге тең болады? Жауабы: 81 (тоғыздық санау системасы).
3.6. Теңдеу біз үшін ойлайды.
Егер сендер теңдеудің кей кездерде біздің өзімізден гөрі алдын ала болжағыштығына күмәнданатын болсандар, мына есепті шығарып көріңдер.
Әкесі 32 жаста, баласы 5 жаста. Қанша жылдан кейін әкесінің жасы баласының жасынан 10 есе үлкен болады?
Ізделіп отырған мерзімді х арқылы белгілейік. х жыл өткен соң әкесі 32 + х, баласы 5+х жаста болады. Әкесінің жасы ол кезде баласының жасынан 10 есе үлкен болуы себепті, мынадай теңдеу шығады:
32+х=10(5+х).
Мұны шешіп, х=-2 болатынын табамыз.
«Минус 2 жылдан соң» деген «екі жыл бұрын» деген сөз. Біз теңдеу құрған кезімізде, болашақта ешқашан әкесінің жасы баласының жасынан 10 есе үлкен бола алмайтынын ескермегенбіз— ондай қатынас тек өткен уақытта ғана болуы мүмкін еді. Теңдеу бізден өткен ойлампаз болды және де өзіміз жіберіп алған ағаттықты ескертті.
3. 7. Төмендегідей қасиеттері бар үш таңбалы сандар:
1) ондық цифры 7;
2) жүздік цифры бірлік цифрынан 4-ке кем;
3) егер осы санның цифрлары кері ретпен орналастырылса, онда жаңа сан ізделіп отырған саннан 396-ға артық болады.
Бірлік цифрын х арқыльг белгілеп, теңдеу құрамыз:
100х + 70 + х−4−[100 (х−4) + 70 + х] = 396.
Бұл теңдеуді ықшамдағаннан соң, мынадай теңдік шығады:
396 = 396.
Оқырмандар бұған қалай түсінік беруді бұрыннан біледі. Бұл бірінші цифры үшінші цифрынан 4-ке кем кез келген үш таңбалы сан цифрларын кері ретпен орналастырғанда 396-ға артатынын білдіреді.
Біз осы кезге дейін аздыкөпті жасанды, кітаптық сипаты бар есептерді қарастырдық; сондағы мақсатымыз — теңдеулер құру мен шешуге дағдыландыру. Енді теория жүзінде түсінік алған соң енді өндіріс саласынан, тұрмыстан, әскери істен, спорттан алынған практикалық есептермен айналысамыз.
3.8. ЕСЕП. «Шаштаразда»
Алгебра шаштаразға керек бола ма? Мұндай жағдай кездеседі екен. Бұған менің көзім жетті, бір күні шаштаразда маған бір шебер тосын өтінішпен үн қатты:
— Біз шеше алмаған есепті шешуге көмектеспес пе екенсіз?
— Осы есепті шеше алмағандықтан қанша ерітіндіні бүлдіріп алдық десеңізші!— деп қостады екіншісі.
— Ол қандай есеп?— деп, мен мән-жайды сұрадым.
— Бізде сутегі асқын тотығының 30-проценттік және 3-проценттік екі ерітіндісі бар. Бұларды 12-проценттік ерітінді шығатындай етіп араластыру керек. Осының дұрыс пропорциясын таба алатын емеспіз...
Маған бір парақ қағаз берді, қажетті пропорция табылды.
Ол пропорция өте қарапайым екен. Атап айтқанда, ол қандай болды екен?
ШЕШУІ: Есепті арифметикалық әдіспен де шешуге болады, бірақ алгебра тілі бұл жерде мақсатқа оп-оңай әрі тез жеткізеді. 12-проценттік қоспа жасау үшін 3-прхоценттік ерітіндіден х грамм, ал 30-проценттік ерітіндіден у грамм алу керек болсын. Сонда бірінші пропорцияда таза сутегінің асқын тотығы 0,03х грамм, екіншіде 0,3у грамм болады, ал барлығы мынаған тең:
0,03х + 0,3y
Осының нәтижесінде (х + у) грамм ерітінді шығады, мұндағы таза сутегінің асқын тотығы 0,12 {х + у) болуы керек.
Мынадай теңдеу шығады: 0,03х + 0,3y = 0,12(х + y).
Осы теңдеуден х = 2у болатынын табамыз, яғни 3-проценттік ерітіндіні, 30-проценттік ерітіндіге қарағанда, екі есе артық алу керек.
3.9. ЕСЕП. «Трамвай мен жаяу адам»
Мен трамвай жолын жағалап жүріп келе жатып, әрбір 12 минут сайын мені бір трамвай қуып жететінін, ал әрбір 4 минут сайын маған бір трамвай қарсы кезігетінін байқадым. Менің де, трамвайдың да жүрісі бір қалыпты.
Трамвай вагондары өздерінің ақырғы пункттерінен бірінен соң бірі қанша минуттан соң шығады?
ШЕШУІ:
Егер вагондар өздерінің ақырғы пункттерінен
әрбір х минуттан соң шығатын болса, онда-
менің трамвайдың бірімен жолығатын жеріме, х минуттан
соң келесі трамвай келеді деген сөз. Егер ол мені қуып
жететін болса, онда ол менің 12 минутта жүріп үлгеретін
жолымды, қалған 12 - х минутта жүріп
өтуі керек . Демек, менің 1 минутта жүретін жолымды
трамвай ![]()
![]() минуттажүреді.
минуттажүреді.
Егер де трамвай маған қарама-қарсы келе жатқан болса, онда ол менің алдыңғы трамвай жолыққаннан кейін 4 минут өткен соң кездестіреді, ал қалған (х—4) минутта ол менің осы 4 минутта жүріп үлгерген жолымды жүріп өтеді. Сондықтан менің 1 минутта жүретін жолымды трамвай
![]() минутта
жүреді..
минутта
жүреді..
Мынадай
теңдеу шығады:![]()
![]()
Бұдан х = 6. Вагондар ақырғы пункттен әрбір 6 минут сайын шығып отырады.
Есептің
төмендегідей (дұрысында арифметикалық) шешуін
ұсынуға болады. Бірінен соң бірі жүретін екі
трамвайдың ара қашықтығын а арқылы
белгілейік. Сонда мені мен маған қарсы келе жатқан
трамвайдың ара қашықтығы бір минутта ![]() -ға
кемиді (себебі қазір ғана кеткен трамвай мен келесі
трамвайдың арақашықтығы а -ға
тең, оны біз 4 минутта жүріп өтеміз). Егер де трамвай мені
артымнан қуып жететін болса, онда біздің ара
қашықтығымыз әр минут сайын
-ға
кемиді (себебі қазір ғана кеткен трамвай мен келесі
трамвайдың арақашықтығы а -ға
тең, оны біз 4 минутта жүріп өтеміз). Егер де трамвай мені
артымнан қуып жететін болса, онда біздің ара
қашықтығымыз әр минут сайын ![]() –ға
кемиді. Енді, мен бір минут алға карай, ал сонан соң кері
қайтып бір минут жүрдім деп жориын (яғни, бастапқы
орынға қайтып келем). Сонда алғашында маған қарсы
келе жатқан трамвай мен менің аралығым бірінші минутта
–ға
кемиді. Енді, мен бір минут алға карай, ал сонан соң кері
қайтып бір минут жүрдім деп жориын (яғни, бастапқы
орынға қайтып келем). Сонда алғашында маған қарсы
келе жатқан трамвай мен менің аралығым бірінші минутта ![]() -ға,
ал екінші минутта (бұл трамвай мені қуып жеткенде)
-ға,
ал екінші минутта (бұл трамвай мені қуып жеткенде) ![]() -ға
кемитін болады. Осының нәтижесінде 2 минутта біздің ара
қашықтығымыз
-ға
кемитін болады. Осының нәтижесінде 2 минутта біздің ара
қашықтығымыз
![]() -ға
кемиді. Егер де мен орнымнан тапжылмай тұра берген болсам да, дәл
осылай болар еді, себебі мен бәрібір кері қайтып келдім ғой.
Сонымен, егер де мен орнымнан қозғалмасам, онда бір минутта (екі
минутта емес) трамвай маған
-ға
кемиді. Егер де мен орнымнан тапжылмай тұра берген болсам да, дәл
осылай болар еді, себебі мен бәрібір кері қайтып келдім ғой.
Сонымен, егер де мен орнымнан қозғалмасам, онда бір минутта (екі
минутта емес) трамвай маған ![]() -ға
жақындай түседі, ал барлық а қашықтықты
ол 6 минутта жүріп өтеді. Бұл орнынан қозғалмай
тұрған бақылаушының қасынан трамвай 6 минут сайын
өтіп тұрады деген сөз.
-ға
жақындай түседі, ал барлық а қашықтықты
ол 6 минутта жүріп өтеді. Бұл орнынан қозғалмай
тұрған бақылаушының қасынан трамвай 6 минут сайын
өтіп тұрады деген сөз.
3.10. ЕСЕП. Пароход пен сал
Пароход А қаласынан өзен ағысының төменгі жағында орналасқан В қаласына дейін (тоқтаусыз) 5 сағат жүзген. Пароход, кері қарай, ағысқа қарсы (әлгіндей меншікті жылдамдықпен әрі тоқтаусыз) 7 сағат жүзген. Сал А -дан В-ге дейін қанша сағат жүзеді (сал өзен ағысының жылдамдығындай жылдамдықпен қозғалады) ?
Ш Е Ш
У I: Пароходтың т ы н ы қ с у д а (яғни меншікті
жылдамдығымен жүзгенде) А -дан 5-ке дейінгі ара
қашықтықты жүзіп өтуге қажет уақытын
(сағат есебімен) х арқылы, ал у арқылы
— салдың жүзу уақытын белгілейік. Пароход бір
сағатта АВ қашықтығының![]() -бөлігін,
ал сал (ағыспен) осы қашықтықтың
-бөлігін,
ал сал (ағыспен) осы қашықтықтың ![]() бөлігін
жүзіп өтеді. Сондықтан пароход өзенмен төмен
қарай бір сағатта АВқашықтығының
бөлігін
жүзіп өтеді. Сондықтан пароход өзенмен төмен
қарай бір сағатта АВқашықтығының ![]() бөлігін,
ал жоғары қарай (ағысқа қарсы)
бөлігін,
ал жоғары қарай (ағысқа қарсы) ![]() бөлігін
жүзеді. Біз есептің шартынан пароход өзенмен төмен
қарай бір сағатта ара қашықтықтың
бөлігін
жүзеді. Біз есептің шартынан пароход өзенмен төмен
қарай бір сағатта ара қашықтықтың ![]() бөлігін,
жоғары қарай
бөлігін,
жоғары қарай ![]() -
бөлігін жүзіп ететінін білеміз.
-
бөлігін жүзіп ететінін білеміз.
Осыдан
мына теңдеулер системасын құрамыз: 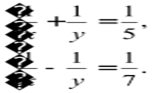
Осы жүйені шешу үшін бөлшектің белімінен арылудың керегі жоқ:
тек бірінші теңдеуден екінші теңдеуді шегеру керек екенін атап керсетеміз. Осының нәтижесінде біз мына теңдеуді шығарып аламыз:
![]() бұдан
у = 35. Сал А -дан В -ге дейін 35сағат
жүзеді.
бұдан
у = 35. Сал А -дан В -ге дейін 35сағат
жүзеді.
ЕСЕП
Ойын-сауық кешінде 20 биші болған. Мария жеті жігітпен, Ольга сегіз жігітпен, Вера тоғыз жігітпен билеген, ал Нинаның өзі жігіттердің барлығымен билеген. Ойын-сауық кешінде қанша биші жігіт болған?
Ш ЕШУ I: Егер белгісізді сәтті таңдап алса, есеп өте оңай шешіледі. Биші жігіттердің саньн емес, биші қыздардың санын іздейміз, оны х арқылы белгілейік:
1- Мария 6+1 жігітпен биледі
2- Ольга 6+2 —»—
3- Вера 6 + 3 —»—
х- Нина 6 + х—»—
Мынадай теңдеу құрамыз: х+(6 +х) =20, бұдан х=7,
сондықтан биші жігіттердің саны : 20-7 = 13.
3.11. ЕСЕП. «Теңіздегі барлау»
Эскадра құрамында жүзіп келе жатқан барлаушыға (барлаушы корабльге) теңіздің эскадра жүзіп келе жатқан бағытындағы 70 миль ауданын тексеріп шығу тапсырылған. Эскадраның жылдамдығы сағатына 35 миль, барлаушының жылдамдығы сағатына 70 миль. Барлаушының қанша уақыттан соң эскадраға қайта оралып келетіндігін анықтау қажет.
ШЕШУІ: Ізделінді сағат санын х арқылы белгілейік. Осы уақытта эскадра 35х миль, ал барлаушы корабль 70х миль жүзіп үлгереді. Барлаушы алға қарай 70 миль және осы жолдың жартысындай жолды кері қарай жүзді, эскадра осы жолдың қалған бөлігін жүзді. Бұлардың екеуі топтасып 70х + 35х жол жүзді, бұл жол 2 • 70 мильге тең. Осыдан мынадай теңдеу құрамыз: .
70х-+35х = 140,
бұдан
![]()
сағат шығады. Барлаушы эскадраға 1 сағ. 20 минуттан соң қайтып оралды.
2- Е С Е П
Барлаушы кеме эскадраның жүзу бағытымен оның алдын барлауға бұйрық алған. Осы кеменің 3 сағаттан соң эскадраға қайтып оралуы қажет. Егер барлаушы кеменің жылдамдығы 60 узел, ал эскадраның жылдамдығы 40 узел болса, барлаушы кеме эскадраны қалдырып кеткен соң қанша уақыт өткенде кері қайтуға тиіс болған?
ШЕ ШУ I: Барлаушы кеме х сағат өткен соң кері қайтуға тиіс болсын; демек, ол эскадрадан х сағат алыстай түсті, ал оған қарай 3 — х сағат жүзді. Барлық корабльдер бір бағытта топтасып жүзіп келе жатқанда, барлаушы кеме х сағатта эскадрадан өздерінің жүзіп үлгерген жолдарының айырмасындай қашықтыққа алыстап үлгереді, яғни 60х — 40х = 20х қашықтыққа алыстайды.
Барлаушы кері қайтқанда эскадраға қарай 60(3—х) қашықтыққа, ал эскадраңың езі 40(3—х) қашықтыққа жузеді. Бұлардың екеуі 10х жолды топтасып жүзді. Сондықтан
60(3-х)+40(3-х)=20х
Бұдан
х=![]() .
.
Барлаушы кеме эскадраны қалдырып кеткенінен кейін 2 сағ 30 минут өткен соң жүзу бағытын кері бағытта езгеотуі қажет.
3.12. ЕСЕ П. «Велодромда»
Велодромның айналма жолымен екі велосипедші бір қалыпты жылдамдықпен жүріп келеді. Егер олар қарама-қарсы бағытта жүретін болса , онда әрбір 10 секунд сайын бір-бірімен кездесетін болған; ал екеуі бір бағытта жүретін болса , онда олардың біреуі екіншісін әрбір 170 секунд сайын қуып жетіп отыратын болған. Егер айналма жолдың ұзындығы 170 м болса, әрбір велосипедшінің жылдамдығы қандай болған?
Ш ЕШУ I: Егер бірінші велосипедшінің жылдамдығы х болса, онда ол 10 секундта 10х метр жүреді. Екінші велосипедші бұған қарама-қарсы жүргенде, бір кездесуден екінші кездесуге дейін жолдың қалған бөлігін, яғни 170―10х метр жүреді. Егер екінші велосипедшінің жылдамдығы 58 у болса, онда бұл жол 10у метр болады; сөйтіп,
170— 10х=10у.
Егер де велосипедшілер бірінің соңынан бірі жүретін болса, онда 170 секундта бірінші велосипедші 170х метр, ал екінші — 170у метр жүреді. Егер бірінші велосипедші екіншіден жылдам жүретін болса, онда бір кездесуден екінщі кездесуге дейін ол, екінші велосипедшіге қарағанда, бір айналым жолды артық жүріп үлгереді, яғни
170х-170у=170.
Бұл теңдеулерді ықшамдағаннан соң мынау шығады:
х + у=17, х-у=1,
бұдан х = 9, у= 8 (секундына метр есебімен)
Қорытынды.
Әр түрлі теңдеулерді шешуді жүзеге асыруда есептеудің тәсілдерін көрсеттім.
Бұл жұмыста біріншіден, теңдеулердің шығару жолдары көрсетіледі.
Екіншіден, ұлттық мазмұнды логикалық есептерді шығарудағы қиыншылықтар, олардың алатын орны көрсетіледі.
Үшіншіден, теңдеулерді шығарудағы есептеудің тәсілдері қарастырылады.
Қазақ халқының математикалық білімінің тамыры терең. Ол қазіргі тілмен алғанда санаудың әртүрлі жүйесін, мәселен үштік пайдаланған. Қазақтың қара есебі өмір қажеттілігінен туындаған. Қазақ халқының тәрбиесінің математикалық астары да түрліше.
Олар: 1. Жұмбақ есеп
2. Өлең есеп
3. Ертегі есеп
Бұл есептерді дұрыс теңдеу құру арқылы шығарсақ, қателеспейміз деп ойлаймын. Ғасырлар бойы даналығымен, өміршеңдігімен дәлелденген халықтық есептер үлгілері- тәрбиенің қайнар көзі болып табылады. Қанша уақыт өтсе де маңызын жоймаған халықтың ұлттық мұрасын тәлім-тәрбиенің түп қазығына айналдыру – біздің де асыл борышымыз. Сондықтан халқымыздың ауыз әдебиетінде, ертегілерде, шешендік тапқыр сөздерінде, салт-дәстүрінде оқушылардың ақыл-ой зердесін тәрбиелеуде ұлттық мазмұнды есептер шығарудың маңызы зор.
Әр баланың мақсаты – өзінің білім деңгейін көтеру, сабаққа деген қызығушылығын арттыру, іздену. Осы мақсатты іске асыру барысындағы міндетім сол тақырыпты игерумен қатар, кең ауқымды есептерді шешуді зерттеу, ойлау қабілетімді машықтыру.
Бұны іске асырудың бір жолы қызықтыратын тапсырмалар таңдай білу. Ойлау барысында менің дербес жұмыс істеу мүмкіндігім, көңіл қоя білу қабілетім дамыды. Математиканың сан алуан сырын, сандар әлемінің қызық құбылысын, ойлау элементтерімен өрнектеген зертеу жұмысы қызықты, әрі ұтымды. Зерттеу барысында жүргізілетін жұмыстар қарапайымнан басталып, біртіндеп қиындап, танымдық қызметін белсендіруге назар аударылады. Зерттеу жұмыстарын жүргізу барысы менің зор ынтамды тудырды, білгенімді тереңдетіп, жаңа іс-қимылға жетеледі
Сондықтанда бұл шығармашылық жұмыс келешекте менің жолдастарыма өз білімдерін тереңдетуіне көмектесетіне сенімдімін.
Ө.Жәнібеков атындағы №4 жалпы орта лицей-интернаты 8«Б» сынып оқушысы Рысбайқызы Жаннаның «Математикалық сауаттылыққа берілген есептердің шешу жолдары және олардың өмірде, тұрмыста қолдану» атты ғылыми жұмысына
Пікір.
Ғылымилық жұмыс кіріспе, зерттеу бөлімі және қорытынды бөлімінен тұрады. Кіріспе бөлімінде теңдеу ұғымы туралы түсінікті, мысалдың шығарылу жолын көрсеткен. Негізгі бөлімінде теңдеулердің қолданылуын, мысалдар арқылы қазақтың байырғы есептерін теңдеу құру арқылы шығарылу жолын толық зерттеген. Жаннаның ғылыми еңбекті жазу барысында қазіргі уақытта математикалық теңдеулерді білмейінше, оны ойдағыдай меңгеру қиын екенін түсіне отырып, бүгінгі күні ғылыми – технологияның дамуына байланысты адамзат баласы ой және дене еңбегін жеңілдететін техникалық құрылғылардың түр-түрін ойлап табудың бәрі адамның ойлау қабілетінің ең ірі жетістіктері екендігіне көз жеткізді. Осы орайда жан-жақты математикалық әдебиеттерден мәліметтер жинақтады.
Рысбайқызы Жанна былтырғы оқу жылынан бастап, тақырып аясында ізденіс жұмыстарын жүргізді.
Математиканың сан алуан сырын, сандар әлемінің қызық құбылысын, ойлау элементтерімен өрнектеген зерттеу жұмысында оқушының жұмыс істеу мүмкіндігі, көңіл қоя білу қабілеті дамыды. Бұл зерттеу жұмысы математика пәнінде кездесетін қиыншылықтардан мүдірмей өтуге және есеп шығарудың жылдамдығын арттыруға көмектеседі.
Белгілі бір жаңа шешу әдістерін меңгеру үшін жан-жақты білім керек.
Көп оқып, ізденудің нәтижесінде есепті жеңіл әрі шапшаң шешуге үйренеді.
Оқушы өзінің ғылыми ізденісінде тақырыпты өзінің құрастырған жоспары бойынша толық талданған.
Бұл ғылыми жағынан да, нақты шығарған есептермен үйлесім тапқан. Өз ойын нақты көрсете білген.
Рысбайқызы Жаннаның еңбегі келешек жас ұрпаққа әсері көп деп білемін.
Математика ғылымы - ғылымдардың негізі екенін түсінген Жанна оқушыма қанаты талмай, биікке самғап, жоғарыдан көріне бер демекпін.
Пікір жазған:
«Ақпараттық технологиялар және энергетика» жоғары мектебі,
«Ақпараттық жүйелеу және модельдеу» кафедрасының доценті,
физика-математика ғылымдарының кандидаты: А.Б.Иманбаева
Абстракт
Бұл жұмыста математикалық теңдеудің өмірмен байланысы туралы баяндалады. Өмірлік мысалдарды қарастыра отырып, оның шешу жолдары көрсетілген. Бұл жұмыс оқушылардың математика пәніне ынтасын, қызығушылығын арттырады.
Абстракт
В этой работе говорится о том, что математические уравнение связаны с жизнью. Раскрыты пути его решение через рассмотрение жизненных примеров. Данная работа повышает интерес к предмету «математика».
Abstract
In this work reports about mathematical equation and its connection with our life. Looking after vital examples we show ways of decision. This work improves the students interests and enthusiasm.
Қолданылған әдебиеттер.
1. Глеман М, Варга Т. Вероятность в играх и развлечениях.- М,
Просвещение, 1979.
2. Тарасов Л.В. Элементы и приложения теории вероятностей в школе. –
М,1996.
3. Математика және физика журналдары
4. С. Ерубаев «Қазақтың байырғы есептері»
5. Ж.А.Елшебай «Зерек» Алматы 1991ж.
6. Т.А.Алдамуратова. Математика 5-сынып
7. П.Я.Депман, Н.Я.Виленкин За старницами учебника математики. М:»Просвещение» 1989г.
8. Математика в школе. Рубрика «Математический календарь» 1985г.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.