methodological_instructions (13)

Methodological Instructions

Theme: Sorting methods

Aim: Implementation of sorting algorithms to solve practical tasks

Assessment criteria

Knowledge

·     Know how data sorted by bubble sort.

Comprehension

·     Understand the mechanism of data moves in bubble sorting

 Application

·     write an algorithm for bubble sort

Language objectives

Learners able to …

• State what bubble sorting  is?

• Describe mechanism of data moves in bubble sorting

Vocabulary and terminology specific to the subject:

Ordered list, unordered list, entry, iteration

Useful expressions for dialogs and letters:

Well, the range of elements needs an order, ascending or … .

For example, every number has its own   … .

Obviously, the sorted data of great convenience for  … .

The list can be sorted …. . The element of list compared with  …  that are in anterior positions. The amount of total steps depends on ….. .

….. .

Theory

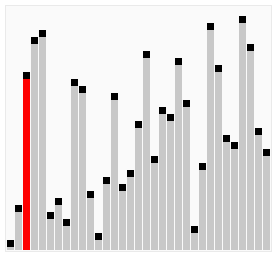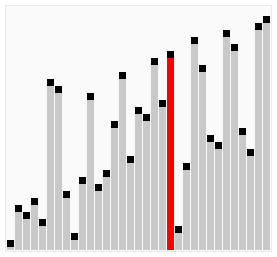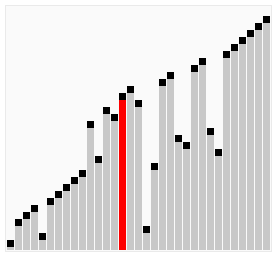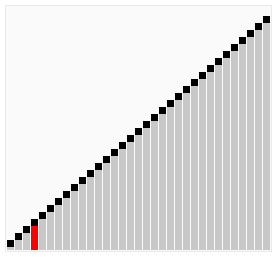
A bubble sort, a sorting algorithm that continuously steps through a list, swapping items until they appear in the correct order.

Bubble sort is a simple sorting algorithm that works by repeatedly stepping through the list to be sorted, comparing each pair and swapping them if they are in the wrong order. The pass through the list is repeated until no swaps are needed, which indicates that the list is sorted. The algorithm gets its name from the way larger elements "bubble" to the top of the list. It is a very slow way of sorting data and rarely used in industry. There are much faster sorting algorithms out there such as insertion sort and quick sort which you will meet in A2.

Step-by-step example

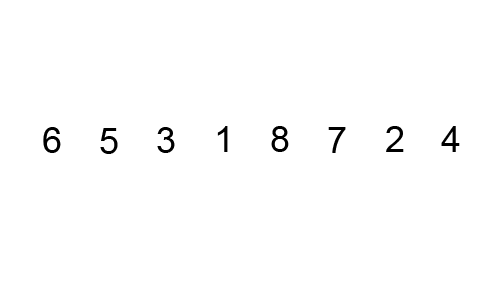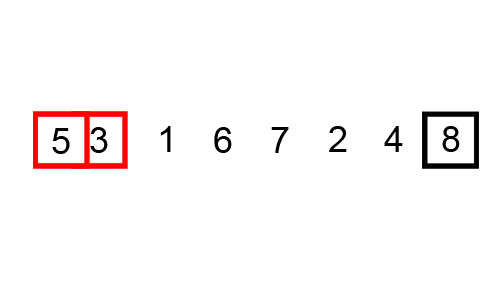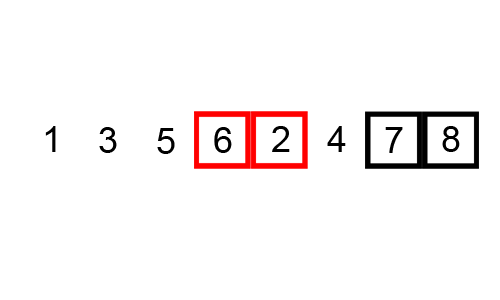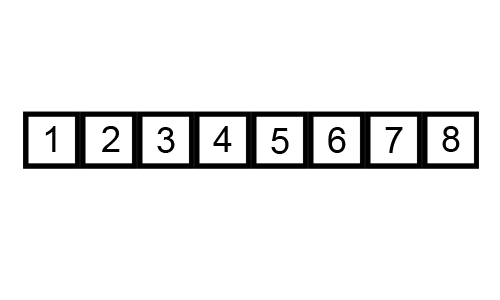
Let us take the array of numbers "5 1 4 2 8", and sort the array from lowest number to greatest number using bubble sort algorithm. In each step, elements written in bold are being compared.

First Pass:
( 5 1 4 2 8 ) {\displaystyle \to } ( 1 5 4 2 8 ), Here, algorithm compares the first two elements, and swaps them since 5 > 1
( 1 5 4 2 8 ) {\displaystyle \to } ( 1 4 5 2 8 ), It then compares the second and third items and swaps them since 5 > 4 
( 1 4 5 2 8 ) {\displaystyle \to } ( 1 4 2 5 8 ), Swap since 5 > 2 
( 1 4 2 5 8 ) {\displaystyle \to } ( 1 4 2 5 8 ), Now, since these elements are already in order (8 > 5), algorithm does not swap them.
The algorithm has reached the end of the list of numbers and the largest number, 8, has bubbled to the top. It now starts again.

Second Pass:
( 1 4 2 5 8 ) {\displaystyle \to } ( 1 4 2 5 8 ), no swap needed
( 1 4 2 5 8 ) {\displaystyle \to } ( 1 2 4 5 8 ), Swap since 4 > 2 
( 1 2 4 5 8 ) {\displaystyle \to } ( 1 2 4 5 8 ), no swap needed
( 1 2 4 5 8 ) {\displaystyle \to } ( 1 2 4 5 8 ), no swap needed
Now, the array is already sorted, but our algorithm does not know if it is completed. The algorithm needs one whole pass without any swap to know it is sorted.
Third Pass:
( 1 2 4 5 8 ) {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) {\displaystyle \to } ( 1 2 4 5 8 )
Finally, the array is sorted, and the algorithm can terminate.

Pseudocode implementation

The algorithm can be expressed as:

procedure bubbleSort( A : list of sortable items )

  do

    swapped = false

    for each i in 1 to length(A) - 1 inclusive do:

      if A[i-1] > A[i] then

        swap( A[i-1], A[i] )

        swapped = true

      end if

    end for

  while swapped

end procedure

П. Questions for self-assessment.

What is the bubble sort?

How to go through passages in bubble sort?

Visual Aids and Materials links.

1.      Slides

2.    https://en.wikibooks.org/wiki/A-level_Computing/AQA/Paper_1/Fundamentals_of_algorithms/Sorting_algorithms

Students' Practical Activities:

Students must be able:

·     write an algorithm for bubble sort

Скачано с www.znanio.ru