
Methodological Instructions
Theme: Algorithms on graphs
Aim: Implementation of search algorithms on graphs to solve the practical tasks
Lesson objective: Searching a Binary Search Tree (BST)
Assessment criteria
Knowledge
· Know the logic of Searching a Binary Search Tree graph
Comprehension
· Describe the logic of Searching a Binary Search Tree graph
Application
· Write program for searching BST graph
Language objectives
Learners able to …
• State what is BST
• Describe the search process in BST graph and its application in Computer Science
Vocabulary and terminology specific to the subject:
Element, binary search tree graph, nodes, path, root, vertices, edge
Useful expressions for dialogs and letters:
Well, searching in binary search tree graph performed in this way … .
For example, to find the element in BST we first need to compare the element with root node. Then ….
Obviously, finding a minimum element in a BST is simple, we just need to access the leftmost element; it is the ….
Theory
Programming Binary Search Tree search
A Binary Search Tree is a binary tree with search properties where elements in
the left sub-tree are less than to the root and elements in the right sub-tree
are greater than to the root.
For example:
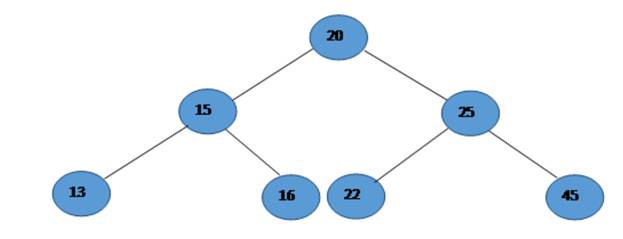
Searching an Element in a Binary Search Tree (BST)
To find an element in a Binary Search Tree, we first need to compare the element with the root node; if it matches then we have the right node otherwise we need to check the left or right.
The C# implementation of that same is as follows.
|
public object SearchElement_Rec(objectelement, TNoderoot) { current = root; if (current == null) return "Not found"; if (Convert.ToInt32(element)== Convert.ToInt32(current.Data)) return element; if (Convert.ToInt32(element)<Convert.ToInt32(current.Data)) return this.SearchElement_Rec(element,current.Left); else returnthis.SearchElement_Rec(element,current.Right); } |
The following is the test result of the implementation.
|
Input: Console.WriteLine(bst.SearchElement_Ite(15)); Output:
Input: Console.WriteLine(bst.SearchElement_Ite(19)); Output: |
Find a Minimum Element in a Binary Search Tree (BST)
Finding a minimum element in a BST is simple, we just need to access the leftmost element; it is the minimum element.
The C# implementation of that is as follows.
|
public object TreeMin_Rec(TNode root) { current = root; if (current.Left == null) { return current.Data; } returnTreeMin_Rec(current.Left); } |
The following is the result of the implementation.
|
Input: Console.WriteLine(bst.TreeMin_Rec(bst.ReturnRoot())); Output: |
Find a Maximum Element in a Binary Search Tree (BST)
Finding a maximum element in a BST is simple, we just need to access the rightmost element; it is the maximum element.
The C# implementation of that is as follows.
|
public object TreeMax_Rec(TNode root) { current = root; if (current.Right == null) { return current.Data; } returnTreeMax_Rec(current.Right); } |
The following is the result of the implementation.
|
Input: Console.WriteLine(bst.TreeMax_Rec(bst.ReturnRoot())); Output: |
Find a Successor Element in a Binary Search Tree (BST)
Finding the successor element is a bit tricky. There can be two cases to consider here.
If the right sub-tree is not null then to find a successor element, we need to find the minimum of the right sub-tree. To find a minimum element of the right sub-tree we can use the TreeMin_Rec method shown above.
If right sub-tree is null then we need to find the successor differently. We need to start from the node (for that we need the successor) and move upwards as long as the current node is on the right of its parent. The moment the current node turns left to its parent, the parent is the successor (if it’s not null).
The C# implementation of that is as follows.
|
public objectTreeSuccessor_Ite(object element) { ////Get the Node object for an element current = this.GetNode(element); if (current!=null) { if (current.Right!= null) returnthis.TreeMin_Rec(current.Right); else { tempParent = current.Parent; while((tempParent != null) && (current == tempParent.Right)) { current = tempParent; tempParent = tempParent.Parent; } if(tempParent != null) returntempParent.Data; else return"Successor is not found!"; } } else { return "Please enter the valid tree element!"; } } |
The following is the result of the implementation. This covers the described two cases (in other words when the right sub-tree is available (element: 20) and when it’s not (element: 16). and when the successor is not available (element: 45).
|
Input: Console.WriteLine(bst.TreeSuccessor_Ite(20)); Output: Input: Console.WriteLine(bst.TreeSuccessor_Ite(16)); Output: Input: Console.WriteLine(bst.TreeSuccessor_Ite(45)); Output: |
Find a Predecessor Element in a Binary Search Tree (BST)
Finding the predecessor element is just the opposite of finding the successor (just interchange the roles of left and right). There can be two cases to consider here as well.
If the left sub-tree is not null then to find a predecessor element, we need to find the maximum of the left sub-tree. To find a maximum element of a left sub-tree we can use the TreeMax_Rec method shown above.
If the left sub-tree is null then we need to find the predecessor differently. We need to start from the node (for that we need the predecessor) and move upwards as long as the current node is on the left of its parent. The moment the current node turns right to its parent, the parent is the predecessor (if it’s not null).
The C# implementationof that is as follows.
|
public objectTreePredecessor_Ite(object element) { ////Get the Node object for an element current = this.GetNode(element); if (current != null) { if (current.Left != null) return this.TreeMax_Rec(current.Left); else { tempParent = current.Parent; while((tempParent != null) && (current == tempParent.Left)) { current = tempParent; tempParent = tempParent.Parent; } if(tempParent != null) returntempParent.Data; else return"Predecessor is not found!"; } } else { return "Please enter the valid tree element!"; } } |
The following is the result of the implementation. This covers the described two cases (in other words when the left sub-tree is available (element: 20) and when it’s not (element: 16) and when the predecessor is not available (element: 13).
|
Input: Console.WriteLine(bst.TreePredecessor_Ite(20)); Output: Input: Console.WriteLine(bst.TreePredecessor_Ite(16)); Output: Input: Console.WriteLine(bst.TreePredecessor_Ite(13)); Output: |
П. Questions for self-assessment.
What we need to do
· to find an element in a Binary Search Tree?
· to find a minimum element?
· to find a maximum element?
· to find a successor element?
Visual Aids and Materials links.
2. https://www.c-sharpcorner.com/UploadFile/19b1bd/binarysearchtreewalkstraversal-implementation-using-C-Sharp/
3. https://en.wikibooks.org/wiki/A-level_Computing_2009/AQA/Problem_Solving,_Programming,_Operating_Systems,_Databases_and_Networking/Programming_Concepts/Tree_traversal_algorithms_for_a_binary_tree
Students' Practical Activities:
Students must be able:
· write program for searching BST graph
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.