Методическая разработка по математике "ИРРАЦИОНАЛЬНЫЕ ЧИСЛА"

Государственное бюджетное профессиональное образовательное учреждение

города Москвы  «Московское среднее специальное училище олимпийского резерва № 2 (колледж)» 

Департамента  спорта города Москвы

Методическая разработка

по математике

тема: ИРРАЦИОНАЛЬНЫЕ ЧИСЛА.

ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ

УПРОЩЕНИЕ ИРРАЦИОНАЛЬНЫХ ВЫРАЖЕНИЙ

(среднее общее образование)

                                            Составитель: Богачёва Т.О., учитель математики

                                                           .

                                               Москва

2021

 ИРРАЦИОНАЛЬНЫЕ ЧИСЛА. ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ

УПРОЩЕНИЕ ИРРАЦИОНАЛЬНЫХ ВЫРАЖЕНИЙ

Краткие теоретические сведения

Иррациональное число – десятичная бесконечная непериодическая дробь.

Иррациональное число нельзя представить в виде отношения  и обратно:  любое число, непредставимое в виде , является иррациональным.

Например:  и т. д.

Решение примеров

№1. Избавиться от иррациональности в знаменателе методом  «домножения»  на сопряжённое число:

       а)   ;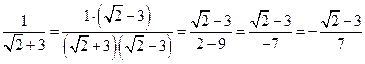

       б)      =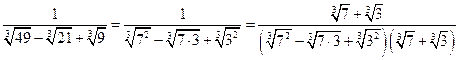 

             .

№2. Упростить выражение методом выделения полного квадрата или куба:

       а)     

            =  = - 2;

       б)   == =

             = .

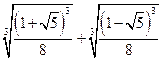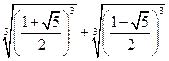 РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ

Краткие теоретические сведения

Формулы применяемые при решении иррациональных уравнений:

1.      ;

2.       ;

3.       ;

4.       ;

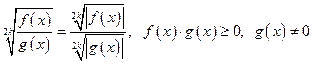5.        .

     и   - некоторые функции, .

Применяя любую из этих формул формально (без учёта указанных ограничений),  следует иметь в виду, что ОДЗ левой и правой частей каждой из них могут быть различными.

  Например, выражение   определено при   и  , а выражение    определено как при  , так и при  .

  При решении иррациональных уравнений необходимо учитывать следующее:

1) если показатель радикала – чётное число, то подкоренное выражение должно быть неотрицательным;

2) если показатель радикала – нечётное число, то подкоренное выражение может быть любым действительным числом; в этом случае знак радикала совпадает со знаком подкоренного выражения.

Рассмотрим уравнения вида

         (1)

Если   , то уравнение не имеет действительных корней.

Если    , то уравнение равносильно системе

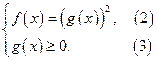
При решении уравнения (1) нет необходимости находить ОДЗ левой части. Достаточно найти корни уравнения (2) и, не прибегая к подстановке в уравнение (1), выяснить какие из найденных корней удовлетворяют неравенству (3).Эти корни, и только они , являются корнями уравнения (1).

  Уравнение вида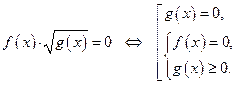 

Если исходное уравнение в процессе преобразований хотя бы один раз заменялось на неравносильное ему следствие, то проверка найденных корней с помощью подстановки является обязательной.

  Уравнение «следствие» получается после преобразований исходного уравнения, при котором имеем корни исходного и ещё посторонний.

Теоремы равносильности

1) если слагаемое перенести из одной части уравнения в другую с переменной знака.

2) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число.

3) возведением обеих частей уравнения в натуральную степень, т.е. переход от уравнения

                к уравнению,    – натуральное, .

Если ,  то  .

Если , то,   

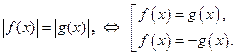
Решение примеров

Доказать, что не имеют решений уравнения:

   а)  .  Арифметический корень не может быть отрицательным числом,

    поэтому, уравнение решений не имеет.

   б)  . 

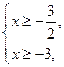
        .  При каждом таком значении  х  величина   

      неотрицательна, а величина    положительна,  следовательно их

     сумма всегда больше нуля. Уравнение не имеет решений.

   в)  .

          не существует такого  х, при котором оба эти 

      выражения имеют смысл. Уравнение решений не имеет.

         Решить уравнение

  №1.   ,

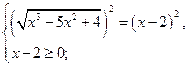
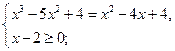
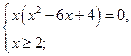
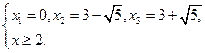
              и меньше 2,   .      

№2.

         ,  замена переменной   .

           , т.к.   то

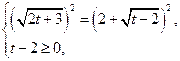
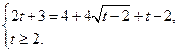
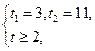               обратная замена:   ,     

  №3.   

  Замена переменной    тогда   , подставим

            т.к.   то  

Т.к.  то уравнение         

№4.   

Возведя обе части уравнения в куб, получим:

Учитывая, что выражение в скобках по условию равно 2, то после приведения подобных слагаемых получим

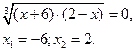                                          {2;-6}