МЕТОДИЧЕСКАЯ РАЗРАБОТКА ПО ПОДГОТОВКЕ К ИТОГОВОЙ АТТЕСТАЦИИ ПО МАТЕМАТИКЕ ДЛЯ УЧАЩИХСЯ 11 КЛАССОВ СВЕДЕНИЕ ЛОГАРИФМИЧЕСКОГО НЕРАВЕНСТВА С ПЕРЕМЕННЫМ ОСНОВАНИЕМ К СИСТЕМЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 3

215116, Смоленская область, г. Вязьма, ул. Докучаева, д. 2     Тел.: директор 8(48131)  6-12-69

Методическая разработка по подготовке к итоговой аттестации по математике для учащихся 11 классов

Сведение логарифмического неравенства с переменным основанием к системе рациональных

неравенств

Малышева Ирина Николаевна

учитель математики высшей категории

2019-2020 уч. г

Сведение логарифмического неравенства с переменным основанием к системе рациональных

неравенств

Пояснительная записка

Цель методической разработки: углубление и расширение знаний по математике, развитие логического мышления и познавательного интереса к предмету.

Основные задачи:

·        подготовить учащихся  к ЕГЭ;

·        подготовить учащихся  к поступлению в ВУЗ;

·        научить решать нестандартные задачи повышенной сложности;

·        расширить представления учащихся о математике как науке.

Актуальность

Задания вида №15 (С3) на ЕГЭ имеют  повышенный уровень сложности и в связи с этим они вызывают затруднения у многих учеников. Чаще  всего это смешанные системы показательных и логарифмических неравенств. Для решения  таких систем необходимо владеть не только методом интервалов, но и многими другими приемами.  Это сопряжено с такими техническими сложностями как: громоздкие выкладки, большие затраты времени (примерное время выполнения 30 мин) и поэтому высока вероятность допустить логическую и вычислительную ошибку.

Новизна

В первой части данной методической разработки рассматривается и доказывается теорема, позволяющая свести логарифмическое неравенство с переменным основанием к системе рациональных неравенств. Приведены примеры решения такого неравенства стандартным методом (школьным) и с помощью теоремы.

Во второй части методической разработки подобраны задачи для организации самостоятельной работы, цель которой - закрепление применения теоремы, усовершенствование навыков по решению подобных неравенств и выход на творческий уровень учебной деятельности.

Практическая значимость

Методическая разработка призвана расширить и углубить  знания учащихся по предмету, позволяет выйти за пределы обязательных знаний. Методическая разработка может быть использована  учителями  в рамках отдельного урока при изучении темы «Решение логарифмических неравенств», и как самостоятельная тема  в рамках уроков подготовки школьников к  ЕГЭ по математике.

Образовательные результаты, формируемые в рамках реализации данной разработки

·        овладение математическими знаниями и умениями, необходимыми для решения логарифмических неравенств с переменным основанием;

·        развитие логического мышления, алгоритмической культуры, математического мышления и интуиции, необходимых  для продолжения образования и для самостоятельной деятельности в области математики и ее приложениях в будущей профессиональной деятельности;

·        овладение навыками компетентности личности в сфере самостоятельной познавательной деятельности;

·        формирование навыков самообразования,  критического мышления, самоорганизации и самоконтроля, умения находить, формулировать и решать проблемы.

I часть

Рассмотрим логарифмическое неравенство вида ,   где ОДЗ неравенства задается системой 

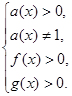
Известен стандартный метод решения такого неравенства: рассмотрение двух случаев на области допустимых значений неравенства.

В первом случае, когда основания логарифмов удовлетворяют условию, знак неравенства изменяется: .

Во втором случае, когда основание удовлетворяет условию , знак неравенства сохраняется: .

При решении мы  рассматриваем два случая и потом объединяем ответы.

Вот уже многие годы при подготовке к ЕГЭ (да и на самом ЕГЭ) моих учеников выручает следующая теорема.

 Теорема. Логарифмическое неравенство

 равносильно следующей системе неравенств:

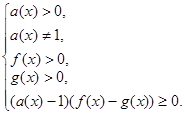
Доказательство: первые четыре неравенства системы задают множество допустимых значений исходного логарифмического неравенства. Обратим внимание на пятое неравенство системы. Если , то первый множитель этого неравенства будет отрицателен. При делении на него придется изменить знак неравенства на противоположный, тогда получится неравенство . Если же , то первый множитель пятого неравенства положителен, сокращаем на него без изменения знака неравенства, получаем неравенство . Таким образом, пятое неравенство системы включает в себя оба  случая предыдущего метода. Терема доказана.

Рассмотрим пример.

Решить неравенство  .

Первый способ.

Стандартный метод решения, который  предполагает разбор двух случаев на области допустимых значений неравенства.

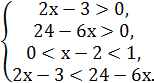  или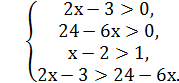

Решаем первую систему: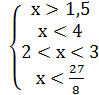, откуда получаем   2

Решаем вторую систему: 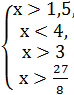 ,   откуда получаем 

Объединяя полученные ответы, имеем окончательное решение данного неравенства.

Ответ:  2

Второй способ.

Применение  теоремы.

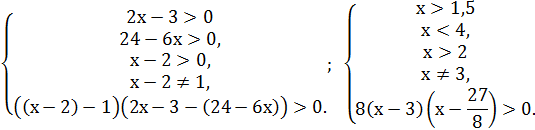
Решив которую, получим  2

Ответ:  2

Итак, применение этой теоремы позволяет существенно упростить решение логарифмического неравенства с переменным основанием и сэкономить время на экзамене.

II часть

Задачи для самостоятельного решения

1.Решить неравенства «методом рационализации»

1.            Ответ:

2.               Ответ:

3.                Ответ:

4.         Ответ:

5.         Ответ:

2. Решить системы неравенств

1.                     Ответ: .

2. 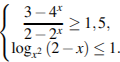                   Ответ:

3. 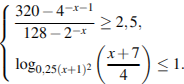                Ответ:

4. 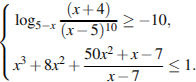                 Ответ:   Ре­аль­ный вариант ЕГЭ 2013

5. 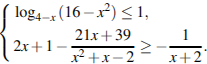                 Ответ: Ре­аль­ный ва­ри­ант ЕГЭ 2013

6. 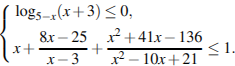                Ответ: (4; 5).Ре­зерв­ный день 19.06.2013.

7. 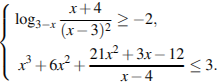                 Ответ: Де­мо­вер­сия 2014.

Источники

1.     Алгебра и начала анализа. 11 класс. В 2 ч. Ч. 1. Учебник для общеобразовательных учреждений (профильный уровень) / Мордкович А.Г., Семенов П.В. - Изд.: Мнемозина, 2010, 287 стр.

2.     Алгебра и начала математического анализа. 11 класс В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений (профильный уровень) / [А. Г. Мордкович, Денищева Л.О., Звавич Л.И. и др. под ред. А. Г. Мордковича. — 3-е изд., стер. — М. : Мнемозина, 2010. — 264 с. : ил.

3.     Колесникова С.И. Решение сложных задач ЕГЭ по математике.9-11 классы. - М.:ВАКО, 2013. – 288 с.- (Мастерская учителя математики).

4.     Методический журнал «Математика» №11 2013г.

5.     Математика. Самое полное издание типовых вариантов заданий ЕГЭ 2012-2014г.  по математике. Под ред. Семенова А.Л., Ященко И.В.

6.     Обучающая система Дмитрия Гущина «РЕШУ ЕГЭ»

Скачано с www.znanio.ru