Методическая разработка практического занятия Тема ”Элементы теории вероятности и математической статистики” (Событие, вероятность события, сложение и умножение вероятностей)

Севастопольское государственное бюджетное образовательное учреждение

профессионального образования

«Севастопольский медицинский колледж имени Жени Дерюгиной»

 

СОГЛАСОВАНО протокол МЦК от ______________2024 г. № Председатель ЦМК ______________Смирнова З. М.

УТВЕРЖДАЮ Зам. директора по учебной работе ________________Полстянко Н.Н. «_____» _______________ 2024 г.

 

 

 

 

 

Методическая разработка

практического занятия

Тема ”Элементы теории вероятности и математической статистики” (Событие, вероятность события, сложение и умножение вероятностей)

 

ОУД 07. Математика

для специальности 34.02.01 «Сестринское дело»

31.02.01 «Лечебное дело»

курс I (база ООО)

 

 

Автор Тищенко Е.Ю.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Севастополь 2024 г.

 

Цель учебного занятия: формирование понятий изучаемых в математической статистике

Задачи:

Образовательные (дидактические):

• сформировать представление о статистике как науке;
• ознакомить студентов с понятием статистика и используемых в ней основными статистическими характеристиками; являющимися основной для развития профессиональных компетенций, предусмотренных ФГОС СПО по специальности (Таблица 1)
• применение знаний в практической деятельности.

Развивающие:

• развивать мыслительную деятельность обучающихся;
• продолжить формирование предметного языка;
• способствовать формированию у обучающихся единой научной картины мира путем выявления межпредметных связей статистики и различных наук.
• развивать общетрудовые и политехнические умения (развитие операционно-контрольных умений – оценивать результаты выполненных действий, регулировать и контролировать свои действия).

Воспитательные:

• воспитывать интерес к изучаемой дисциплине, информационную культуру; готовность к выполнению общепринятых норм и правил, высокой работоспособности и организованности
• развитие общих компетенций (Таблица 2.)

Формы организации учебной деятельности:

• фронтальная работа
• индивидуальная работа.

Таблица 1. Результаты обучения на учебном занятии

Таблица 2. Формируемые общие компетенции на учебном занятии

Тип урока: урок изучения нового материала

Педагогическая технология (ее элементы): технология модульного обучения информационно-коммуникационные технологии

Таблица 3. Методы обучения, используемые на учебном занятии

 

 

Цель учебного занятия:- формирование понятий изучаемых в математической статистике

Задачи:

Образовательные (дидактические):

• сформировать представление о статистике как науке;
• ознакомить студентов с понятием статистика и используемых в ней основными статистическими характеристиками; являющимися основной для развития профессиональных компетенций, предусмотренных ФГОС СПО по специальности (Таблица 1)
• применение знаний в практической деятельности.

Развивающие:

• развивать мыслительную деятельность обучающихся;
• продолжить формирование предметного языка;
• способствовать формированию у обучающихся единой научной картины мира путем выявления межпредметных связей статистики и различных наук.
• развивать общетрудовые и политехнические умения (развитие операционно-контрольных умений – оценивать результаты выполненных действий, регулировать и контролировать свои действия).

Воспитательные:

• воспитывать интерес к изучаемой дисциплине, информационную культуру; готовность к выполнению общепринятых норм и правил, высокой работоспособности и организованности
• развитие общих компетенций (Таблица 2.)

Формы организации учебной деятельности:

• фронтальная работа
• индивидуальная работа.

Таблица 1. Результаты обучения на учебном занятии

Таблица 2. Формируемые общие компетенции на учебном занятии

Тип урока: урок изучения нового материала

Педагогическая технология (ее элементы): технология модульного обучения информационно-коммуникационные технологии

Таблица 3. Методы обучения, используемые на учебном занятии

 

 

Эпиграф к занятию:

Еще в 1888 году Менделеев Д.И. сказал:
“Грубую форму статистики
поэты когда-нибудь облекут в стихи,
потому что цифрами открывается сила,
власть, людские слабости
и много других сторон мира”.
Технологическая карта занятия

 

 

 

 

 

Теория вероятностей.

Теория вероятностей есть математическая наука, изучающая закономерности в случайных явлениях.

Случайное явление – это такое явление, которое при неоднократном воспроизведении одного и того же опыта протекает каждый раз несколько по-иному.

Опытом называется всякое осуществление определенного комплекса условий, при которых наблюдается соответствующее явление.

Под событием в ТВ понимается всякий факт, который в результате опыта может произойти или не произойти.

Событие называется достоверным, если оно обязательно произойдет в этом опыте.

Пример. Выпадение не более 6 очков игральной костью.

Событие называется невозможным, если в данном опыте оно произойти не может.

Пример. Выпадение 8 очков одной игральной костью.

Событие называется случайным, если в данном опыте может произойти или не произойти.

Пример. Стрельба по мишени.

Два события называются совместными в данном опыте, если появление одного из них не исключает проявления другого.

Пример. Выпадение четного числа очков.

Два события называются несовместными в данном опыте, если они одновременно не могут произойти.

Пример. Выпадение герба и решки.

Несколько событий образуют полную группу, если в результате испытаний обязательно произойдет хотя бы одно из них.

Несколько событий в данном опыте называются равновозможными, если по условиям симметрии есть основание считать, что ни одно из этих событий не является более возможным чем другое.

Пример. Выпадение 1, 3, 5 на кости.

Если события, образующие полную группу, являются равновозможными и попарно несовместными, то такие события принято называть случаями, а группу таких событий – схемой случаев.

 

§1. Классический метод вычисления вероятности.

1.     Классическая вероятность.

Случай называется благоприятным некоторому событию, если появление этого случая влечет за собой появление данного события.

Например, при бросании игральной кости возможны шесть случаев; из них событию А – появлению четного числа очков – благоприятны три случая: 2, 4, 6 и неблагоприятны остальные три.

Вероятностью события называется отношения числа благоприятных случаев к общему числу случаев. Вероятность события А обозначим через ; тогда по определению

 ,                                                                    (1)

где m – число благоприятных событию А случаев, n – общее число случаев.

Формула (1) известна как классическое определение вероятности. Она пригодна тогда и только тогда, когда опыт сводится к схеме случаев, т.е. преимущественно в искусственно организованных опытах, в которых заранее и сознательно обеспечена одинаковая возможность исходов опыта.

§2. Геометрическая вероятность.

В случае когда число исходов опыта бесконечно и все исходы заполняют некоторую ограниченную область, используют геометрический метод вычисления вероятности.

В общем случае геометрическая вероятность равна отношению меры (объема, площади, длины) рассматриваемой части области к мере всей области.

§3. Частота события. Статистическое определение вероятности.

Далеко не всякий опыт может быть сведен к схеме случаев или к геометрической вероятности. Пусть, например, игральная кость несимметрична, значит, какая-то ее грань будет выпадать чаще остальных, т.е. события, заключающиеся в появлении различных граней, неравновозможны. Но тем не менее и в этом случае для каждой грани существует своя определенная степень объективной возможности ее появления.

Пусть произведена серия из n опытов, в каждом из которых могло появиться событие А.  Относительной частотой события А в данной серии опытов называется отношение числа опытов, в которых появилось событие А, к общему числу произведенных опытов:

                                                                        (2)

где m – число появлений события А , n – общее число опытов.

Конечно, частота может изменяться от одной группы опытов к другой. Но наблюдения позволили установить, что относительная частота обладает свойством статической устойчивости: в различных сериях многочисленных испытаний она принимает значения, достаточно близкие к некоторой постоянной. Эту постоянную и считают вероятностью данного события.

Итак, вероятностью события называется число, около которого группируются значения относительной частоты данного события в различных сериях большого числа испытаний.

Если, например, вы бросаете монету, то чем большее количество бросков будет проделано, тем более относительная частота выпадения герба близка к . Читателям предлагается экспериментально убедиться в правомерности сказанного, откуда будет следовать, что вероятность выпадения герба равна 0,5. для этого бросьте монету сначала 10 раз и сосчитайте, сколько раз выпал герб, затем – 100, 200, 300, 400 раз с подсчетом каждый раз числа выпадения герба.

Приведенное определение вероятности называется статистическим. Как и в случае классического определения, сохраняются свойства вероятности:

1)      значение вероятности заключено между нулем и единицей;

2)      вероятность невозможного события равна нулю;

3)      вероятность достоверного события равна единице.

Каждое массовое явление обладает определенной характеристикой, выражающей степень возможности его осуществления и называемой вероятностью. Подчеркнем, что вероятность – теоретическая характеристика исследуемого факта; она заключена в самой природе явления.

Человечество имеет дело практически с частотой происходящих событий. Но при большом количестве исследуемых фактов относительная частота очень близка к вероятности. Это обстоятельство выражено в теореме Бернулли, утверждающей, что при достаточно большом числе опытов вероятность события, заключающегося в том, что разность между частотой события и его вероятностью становится сколь угодно малой, неограниченно приближается к единице. В этом случае говорят, что имеет место сходимость вероятности. Данная теорема связанна с законом больших чисел, согласно которому при очень большом числе случайных явлений средний их результат практически перестает быть случайным и может быть предсказан с большой степенью определенности. Именно поэтому возможно статистическое определение вероятности. Частота – это характеристика, в которой «проявляется», «высвечивается» вероятность.

Деловые люди (Например, работники обществ) широко используют этот закон. Вот что писал по этому поводу известный специалист по психологии общения Дейл Карнеги: «Самая знаменитая страховая компания «Ллойд» в Лондоне нажила бесчисленные миллионы на склонности людей беспокоиться о том, что случается очень редко. Лондонская компания «Ллойд» держит пари с людьми, которые к ней обращаются, что несчастье, о которых они беспокоятся, никогда не произойдут. Однако фирма не называет это «держать пари». Они называют это страхованием. Но на самом деле она действительно держит пари исходя из закона больших чисел. Это огромная страховая компания процветает уже 200 лет. И если не изменится человеческая натура, компания будет существовать и процветать и еще 50 веков, занимаясь страхование обуви и кораблей от несчастных случаев, которые по закону больших чисел происходят совсем не так часто, как мы воображаем».

§4. Основные теоремы теории вероятностей.

1.     Операции над событиями.

Суммой двух событий называется событие, состоящее в появлении хотя бы одного из них. Например, если событие А – попадание в цель при первом выстреле, событие В – попадание в цель при втором выстреле, то событие есть попадание в цель вообще, безразлично при каком выстреле – при первом, при втором или при обоих вместе. Аналогично суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.

Произведением двух событий А и В называется событие С, состоящее в совместном выполнении события А и события В. например, если событие А – появление «дамы» при вынимании карты из колоды, В – появление каты пиковой масти, то событие - появление пиковой дамы. Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

Событие  называется противоположным для А, если оно выполняется тогда и только тогда, когда не выполняется событие А. Например, А – «выпадение «орла»»,  -«выпадение «решки»» при одном бросании монеты; А – «сдача экзамена»,  - «не сдача экзамена».

При вычислении вероятностей часто бывает удобно представлять сложные события в виде комбинации более простых событий, применяя операции сложения и умножения событий, а также противоположное событие. Пусть, например, по мишени производится три выстрела, и рассматриваются следующие элементарные события:

 - попадание при первом выстреле;

 - промах при первом выстреле;

 - попадание при втором выстреле;

- промах при втором выстреле;

 - попадание при третьем выстреле;

 - промах при третьем выстреле.

Если сложное событие В состоит в том, что в результате этих трех выстрелов будет только одно попадание, то это событие выразится в виде:

Перечислим свойства операций над событиями:

1.

2.   - коммутативность.

3. , - ассоциативность.

4.  - дистрибутивность.

5. ,  - аналог законов Де Моргана.

6., .

7. , .

8. ,.

9. , .

В свойствах 7, 8, 9 U – достоверное событие, V – невозможное событие.

Перейдем к вопросу определения вероятности произвольных событий.

2.     Теорема сложения вероятностей.

Пусть события А и В несовместны. Тогда теорема сложения формулируется так:

Теорема. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:

.                                                                (3)

Доказательство. Обозначим: n – общее число возможных исходов; m – число исходов, благоприятных событию А; k – число исходов, благоприятных событию В. Тогда

 ; .

По условию события А и В несовместны. Значит, случаев, благоприятных А и В вместе, нет. Поэтому  благоприятных  случаев и

.

И, следовательно, .

Теорема легко обобщается на случай несколько попарно несовместных событий. Например, .

Следствие1. Если попарно несовместные события образуют полную группу несовместных событий, то сумма их вероятностей равна единице.

Доказательство. Так как события образуют полную группу, то появление хотя бы одного из них – достоверное событие:

.

Так как  - несовместные события, то к ним применима теорема сложения вероятностей:

.                                (4)

Следствие 2. Сумма вероятностей противоположных событий равна единице:

.                                                                 (5)

Например, если - вероятность записи нейронной активности клеток «внимания», то - вероятность записи для клеток другого вида активности.

Если же события А и В совместны, то теорема сложения формулируется следующим образом:

Теорема. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления, т.е.

                                                   (6)

Доказательство. Пусть n – общее число исходов опыта; m – число случаев, благоприятных событию А; k – число случаев, благоприятных событию В; l – число случаев, благоприятных событию А, и событию В. Тогда  ; ; .

В сумме m+k дважды учтены исходы, благоприятные событию АВ. Поэтому число опытов, благоприятных событию А+В, будет m+k-l. Таким образом,

3.     Условная вероятность. Теорема умножения вероятностей.

Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Пусть, например, в урне пять шаров – два белых и три черных. Два человека вынимают из урны по одному шару. Рассмотрим события:

А – появление белого шара у первого человека.

В - появление белого шара у второго человека.

Вероятность события А до того, как стало известно что-либо о событии В, равна 2/5. если стало известно, что событие В произошло, она равна ¼. Так как эти вероятности не равны, заключаем, что событие А зависит от события В.

Вероятность события А, вычисленная при условии, что имеет место событие В, называется условной вероятностью события А и обозначается . Для данного примера Р(А)=2/5; Р(А/В)=1/4.

Итак, если событие А зависит от события В, то Р(А)≠Р(А/В). Если же событие А не зависит от события В, то Р(А)=Р(А/В). В этом случае событие В никак не влияет на вероятность события А и условная вероятность равна безусловной.

Пусть события А и В образуют полную группу и событию А благоприятствует m случаев, событию В - k случаев, событию АВ – l случаев, а общее число случаев равно n. Тогда

Р(А)=m/n;  P(AB)=l/n.

Вычислим Р(В/А), т.е. условную вероятность события В в предположении, что А произошло. Но если мы знаем, что событие А появилось, то из ранее возможных n случаев остаются возможными только m случаев, которые благоприятны событию А. Из них l случаев благоприятны событию В. Значит,

Р(В/А)=l/n.

Преобразуем полученное выражение:

Р(В/А)=l/n=(l/n)/(m/n)=Р(АВ)/Р(А).

Отсюда следует теорема умножения вероятностей:

Р(АВ)=Р(А)Р(В/А),                                                             (7)

т.е. вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло.

Применяя (7) к событию ВА, получаем

Р(ВА)=Р(В)Р(А/В)

и, поскольку АВ=ВА, имеем

Р(АВ)=Р(В)Р(А/В).

Из (7)  и (3) следует , что

Р(А)Р(В/А)=Р(В)Р(А/В).

Поэтому если А не зависит от В, т.е. Р(А)= Р(А/В), то Р(В)= Р(В/А) и В не зависит от А. таким образом, можно говорить о независимых событиях А и В.

Так как  для независимых событий условная вероятность равна безусловной, то для таких событий

Р(АВ)=Р(А)Р(В).                                                             (8)

Полученная теорема может быть обобщенна на любое число событий. В частности, для трех событий А, В, С:

Р(АВС)=Р(А)Р(В/А)Р(С/АВ).                                                 (9)

Если рассматриваются три события и более, то события называются независимыми в совокупности, если они попарно независимы и каждое из них не зависит от произведения любого набора из остальных событий. Для таких событий вероятность произведения равна произведению вероятностей сомножителей.

Теорема умножения вероятностей в некоторой мере объясняет так называемый закон всеобщей подлости, частным проявлением которого является падение бутерброда маслом вниз. Не вдаваясь в физическую сущность вопроса, рассмотрим этот закон с психо-математической точки зрения.

Указанный закон вступает в действие, когда человек очень ждет совершения чего-то, какого-то события. Этому событию предшествует множество условий, как, впрочем, и с любым событием связано множество условий, как, впрочем, и с любым событием связанно множество условий, которые остаются без внимания, если событие не интересует, и начинают играть доминирующую роль в случае заинтересованности в данном событии.

Однако при достаточно большой вероятности каждого условия, равной 0,9, уже при 4 таких условиях вероятность их совместного выполнения будет не более т.е. в среднем не более, чем в 66% случаев, возможно осуществление необходимых условий для ожидаемого события.

 

4.     Вероятность появления хотя бы одного события.

Пусть - независимые в совокупности события; - противоположные им события (также независимые).

Обозначим через В событие, состоящее в том, что произошло хотя бы одно из событий . Событие, противоположное В, будет состоять в том, что не произошло ни одного события из перечисленной группы, т.е.

Но так как В и являются противоположными событиями, то

Р(В)+Р()=1

и

Р(А)=1-Р()=1-.

Иногда удобно обозначить вероятность события через , а вероятность - через  (). Понятно .

Тогда можно записать, что

Р(В)=1-.                                                                (10)

А если , то

Р(В)=1-.                                                                        (11)

 

§5. Следствия теорем сложения и умножения.

1.     Формула полной вероятности.

Пусть событие А может произойти только в случае наступления одного из событий , образующих полную группу.

Эти события будем называть гипотезами. Вероятность события А в этом случае находится по формуле:

,

или

                                                      (12)

Формулу (12) называют формулой полной вероятности. Докажем ее.

Доказательство. Событие А можно представить в виде суммы попарно несовместных событий

.

Значит, . Так как события  () несовместны, то:

.

По (7) вероятность  , откуда и получаем (12).

2.     Формула Байеса.

События  при наступлении которых происходит событие А, мы называем гипотезами. Каждая из гипотез имеет свою вероятность, вычисленную до опыта, в котором может произойти событие А. А как влияет появление события А на вероятность гипотез? Меняется ли эта вероятность после опыта?

Из теоремы умножения имеем:

,

Приравняем правые части полученных равенств:

  (),

Откуда

  (),                                                  (13)

 

 

где Р() – априорная вероятность i-ой гипотезы, - апостериорная вероятность той же гипотезы, Р(А) вычисляется по формуле полной вероятности (12).

Таким образом,

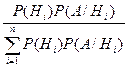  (),                                                  (14)

Формулы (13) или (14) называются формулами Байеса. Они позволяют осуществить переоценку вероятностей гипотез. Это дает возможность корректировать управленческие решения, оценки неизвестных параметров распределения и т.д.

 

§6. Принятие решений на основе байесовских стратегий.

Постановка задачи заключаются в следующем. Имеются две альтернативные гипотезы и .

Например, - на должность заместителя директора подходит кандидатура Смирнова; -  на должность заместителя директора подходит кандидатура Егорова.

На основе мнения сотрудников, статистических данных и иных данных задаются вероятности этих гипотез. В рамках каждой гипотезы рассматриваются все возможные последствия, на основе которых по формулам Байеса происходит уточнение вероятностей гипотез.

Какую из гипотез выбрать: гипотезу, имеющую большую вероятность или гипотезу с меньшей вероятностью?

Конечно, более достоверна гипотеза с большей вероятностью. Однако на самом деле может иметь место как раз гипотеза с меньшей вероятностью. Поэтому при выборе гипотез можно совершить ошибку. Например, с точки зрения общества обвинить невинного человека хуже, чем оправдать виновного. Для учета этого обстоятельства вводятся коэффициенты  и , характеризующие соответственно величину ошибок при принятии гипотез вместо и вместо. Эти коэффициенты называются также коэффициентами сожаления. Пусть событие Е характеризуют данные, относящиеся к делу.

Для каждой гипотезы и  вычисляется так называемый байесовский риск, обозначаемыйи  соответственно. А именно:

 и ,

где характеризует величину риска при выборе гипотезы , - при выборе гипотезы .

Далее выбирается та гипотеза, для которой указанный риск является наименьшим.

Мы рассмотрели случай двух альтернативных гипотез. В общем случае все рассуждения проводятся совершенно аналогично. Например, в случае трех гипотез вводятся коэффициенты сожаления , которые характеризуют ошибку принятия гипотезы  вместо гипотезы . Затем вычисляются риски:

;

;

;

Принимается гипотеза, для которой величина риска наименьшая.

Рассмотренный метод дает возможность прогнозировать оптимальные стратегии и соответственно планировать действия.

В рассмотренном примере не учитывался приоритет исходных данных . Однако можно было задать коэффициенты приоритета этих условий.

В случае наличия приоритетов вероятность каждого условия умножается на соответствующий коэффициент, а далее все вычисления проводятся согласно рассмотренному методу.

 

 §7. Понятие случайной величины. Дискретные случайные величины и их законы распределения.

Случайной величиной называется величина, которая в результате опыта может принять определенное значение.

Дискретной называют случайную величину, возможные значение которой есть отдельные изолированные числа. Например, число студентов в аудитории, количество положительных тестов в психодиагностике и т.д.

Непрерывной называется случайная величина, которая может принимать любое значение из некоторого конечного или бесконечного промежутка, т.е. возможные значения непрерывно заполняют некоторый промежуток. Например, величина светоощущения в психодиагностике, скорость космического аппарата, ошибка взвешивания на точных весах и т.д.

Случайные величины обозначаются буквами X, Y, Z, а их возможные значения – буквами x, y, z. Запись Х=х означает, что случайная величина Х приняла значение х, запись Р(Х=х) означает вероятность того, что Х приняла значение х.

Непрерывные случайные величины будут рассмотрены далее. Сейчас обратимся к дискретным случайным величинам.

Каждое значение дискретной случайной величины появляется с некоторой вероятностью. Эти значения сопоставляются в законе распределения со своими вероятностями.

Законом распределения дискретной случайной величины называется перечень ее возможных значений и соответствующих им вероятностей. О случайной величине говорят, что она подчинена данному закону распределения. Простейшей формой задания этого закона является таблица, называемая рядом распределения, в которой перечислены возможные значения случайной величины и соответствующие им вероятности.

 

Так как в каждом испытании случайная величина Х принимает одно и только одно возможное значение, события Х=х₁, Х=х₂, ..., Х=х_n образуют полную группу, и , значит, сумма вероятностей равна единице:

++...+=1.

Другая форма закона распределения – функция распределения F(x), которая представляет собой вероятность того, что случайная величина Х примет значение, меньше х, т.е.

 F(x)=Р(Х<х).                                                                    (15)

Функцию распределения иногда называют интегральной функцией распределения.

Функция распределения любой дискретной случайной величины представляет собой ступенчатую функцию со скачками в точках значений случайной величины. Скачки равны вероятностям этих значений. Сумма всех скачков равна 1.

Функция распределения любой случайной величины обладает следующими свойствами, которые следуют из ее определения:

1.      Множество значений F(х) содержится на отрезке [0;1]:

2.      Функция распределения есть неубывающая функция, т.е. если , то

3.      Если все возможные значения принадлежат интервалу (а,b), то F(х)=0 при , F(х)=1 при .

4.      Для  F(х) выполняются предельные соотношения:

;

5.      Функция распределения непрерывна слева:

6.      Если , то  

Пусть  и  Тогда

 

ВАРИАНТЫ

 

Вариант 1. 1.На рисунке показана схема лесных дорожек. Пешеход идет из точки S по дорожкам, на каждой развилке выбирая дорожку случайным образом и никогда не возвращаясь обратно. Найдите вероятность того, что он попадет в точку M. 2. Лампы определенного типа выпускают только два завода. Первый завод выпускает 40% ламп, второй—60%. Среди продукции первого завода 2% бракованных ламп, среди продукции второго—3%. Найдите вероятность того, что случайно купленная в магазине лампа этого типа окажется исправной. 3. Стрелок 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,7. Найдите вероятность того, что стрелок попал в мишень один раз и 3 раза  промахнулся. 4. Ковбой Джон попадает в муху на стене с вероятностью 0,8, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 2 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся. 5. Виолетта бросила одновременно две игральные кости и ни на одной не выпало шесть очков. Какова вероятность при этом условии, что в сумме выпало 4 очка? 6. На диаграмме Эйлера показаны события A и B в некотором случайном эксперименте, в котором 15 равновозможных элементарных событий. Элементарные события показаны точками. Найдите Р(В/А)— условную вероятность события B при условии A.	Вариант 2. 1. На рисунке показана схема лесных дорожек. Пешеход идет из точки S по дорожкам, на каждой развилке выбирая дорожку случайным образом и не возвращаясь обратно. Найдите вероятность того, что он попадет в точку F. 2. Две фабрики одной фирмы выпускают одинаковые мобильные телефоны. Первая фабрика выпускает 30% всех телефонов этой марки, а вторая—остальные телефоны. Известно, что из всех телефонов, выпускаемых первой фабрикой, 1% имеют скрытые дефекты, а у выпускаемых второй фабрикой—1,5%. Найдите вероятность того, что купленный телефон этой марки имеет скрытый дефект. 3. Стрелок 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,7. Найдите вероятность того, что стрелок первые 3 раза попал в мишени, а последний раз промахнулся. Результат округлите до тысячных. 4.Робин Гуд подошел к столу, на котором лежали 3 его старых лука и 2 новых. Он решил сбить стрелой яблоко с дерева. Робин попадает в цель из старого лука с вероятностью 0,8. А из нового- с вероятностью 0,3. Робин случайным образом выбирает один лук. Найдите вероятность того, что Робин промахнется при стрельбе. 5.Егор подбрасывает игральный кубик дважды. В сумме у него выпало 9 очков. Найдите вероятность того, что хотя бы раз выпало 5 очков. 6. На диаграмме Эйлера показаны события A и B в некотором случайном эксперименте, в котором 10 равновозможных элементарных событий. Элементарные события показаны точками. Найдите Р(В/А)— условную вероятность события B при условии A.
Вариант 3. 1.     Гусеница ползет вверх по ветви куста. На каждой развилке гусеница с равными шансами может попасть на любую из растущих веточек. Найдите вероятность того, что гусеница доберется до одного из листьев. 2. Два завода выпускают одинаковые подшипники. Первый завод выпускает 38% подшипников, второй—62%. При проверке оказалось, что 2%  продукции первого завода и 2,5% второго имеют скрытые дефекты . Найдите вероятность того, что случайно купленный подшипник окажется бракованным. 3. Стрелок стреляет по одному разу в каждую из 4-х мишеней. Вероятность попадания в мишень при каждом отдельном выстреле равна 0,8. Найдите вероятность того, что стрелок попадет в 3 первые мишени и не попадет в последнюю. 4. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,1. На столе лежит 10 револьверов, из них только 3 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся. 5. Игральную кость бросили два раза. Известно, что 6 очков не выпало ни разу. Найдите при этом условии вероятность события «сумма очков равна 8». 6. На диаграмме Эйлера показаны события A и B в некотором случайном эксперименте, в котором 15 равновозможных элементарных событий. Элементарные события показаны точками. Найдите Р(А/В)— условную вероятность события А при условии В.	Вариант 4. 1.На рисунке показана схема лесных дорожек. Пешеход идет из точки S по дорожкам, на каждой развилке выбирая дорожку случайным образом и не возвращаясь обратно. Найдите вероятность того, что он попадет в березовую рощу, обозначенную на схеме закрашенной областью. 2.  Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 25%  этих стекол, вторая – 75%.  Первая фабрика выпускает 4%  бракованных стекол, а вторая – 2%.  Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным. 3. Биатлонист 6 раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние три промахнулся. Результат округлите до тысячных. 4. Робин Гуд подошел к столу, на котором лежали 2 его старых лука и 2 новых. Он решил сбить стрелой яблоко с дерева. Робин попадает в цель из старого лука с вероятностью 0,7. А из нового- с вероятностью 0,4. Робин случайным образом выбирает один лук. Найдите вероятность того, что Робин промахнется при стрельбе. 5. Игральную кость бросили два раза. Известно, что 2 очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 4». 6. На диаграмме Эйлера показаны события A и B в некотором случайном эксперименте, в котором 10 равновозможных элементарных событий. Элементарные события показаны точками. Найдите Р(А/В)— условную вероятность события А при условии В.
Вариант 5. 1.На рисунке показана схема лесных дорожек. Пешеход идет из точки S по дорожкам, на каждой развилке выбирая дорожку случайным образом и не возвращаясь обратно. Найдите вероятность того, что он попадет в грибное место, обозначенное на схеме закрашенной 6бластью. 2. Две фабрики выпускают одинаковую стеклянную  посуду. Первая фабрика выпускает 45% блюдец, вторая – 55%.  Первая фабрика выпускает 1%  бракованных блюдец, а вторая – 3% Найдите вероятность того, что случайно купленное в магазине блюдце окажется бракованным. 3. Стрелок 5 раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,9. Найдите вероятность того, что стрелок попал в мишень 2 раза и 3 раза промахнулся. 4. Ковбой Джон попадает в муху на стене с вероятностью 0,7, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,1. На столе лежит 10 револьверов, из них только 2 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся. 5. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет ровно один раз. 6. На диаграмме Эйлера показаны события A и B в некотором случайном эксперименте, в котором 15 равновозможных элементарных событий. Элементарные события показаны точками. Найдите Р(В/А)— условную вероятность события B при условии A.	Вариант 6. 1. Гусеница ползет вверх по ветви куста. На каждом разветвлении гусеница с равными шансами может попасть на любую из растущих веточек. Какова вероятность того, что гусеница попадет в точку A? 2. Две фабрики выпускают одинаковые стёкла для автомобильных фар. Первая фабрика выпускает 45% этих стёкол, вторая — 55%. Первая фабрика выпускает 1% бракованных стёкол, а вторая — 3%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным. 3. Биатлонист 3 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последний раз промахнулся. Результат округлите до сотых. 4. Ковбой Джон попадает в муху на стене с вероятностью 0,8, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,4. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся. 5. Игральный кубик бросают 2 раза. С какой вероятностью выпавшие числа будут отличаться на 3? Ответ округлите до сотых. 6. На диаграмме Эйлера показаны события A и B в некотором случайном эксперименте, в котором 10 равновозможных элементарных событий. Элементарные события показаны точками. Найдите Р(В/А)— условную вероятность события B при условии A.

 

Задача 1. В соревнованиях по плаванию участвуют 4 спортсмена из Германии, 6 спортсменов из Италии, 7 спортсменов из России и 5 из Китая. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что спортсмен из Италии Джованни Лучио будет выступать первым, вторым или третьим.

Решение.

Здесь мы сразу видим союз «или» в формулировке задачи «найти вероятность, что спортсмен будет   выступать или первым или вторым или третьим». Этот союз означает сложение следующих событий:

A: Джованни Лучио будет выступать первым;

B: Джованни Лучио будет выступать вторым;

C: Джованни Лучио будет выступать третьим.

Так как речь идет о конкретном спортсмене, то число благоприятных исходов для него, равно . Всего же равновероятных исходов . Получаем вероятности появлений событий A, B и C:

Учитывая, что эти события несовместны (Джованни Лучио не может одновременно выступать на двух местах), получаем значение искомой вероятности:

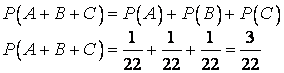
Ответ: 3/22.

 

Задача 2. В соревнованиях по плаванию участвуют 4 спортсмена из Германии, 6 спортсменов из Италии, 7 спортсменов из России и 5 из Китая. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что спортсмены из Италии будут выступать первыми или вторыми.

Решение.

Видите? Здесь речь идет уже не о конкретном пловце, а обо всех спортсменах из Италии. И это кардинально меняет решение, так как следующие события становятся совместными:

A: на первом месте выступает пловец из Италии;

B: на втором месте выступает пловец из Италии.

Нам нужно найти вероятность , которая для совместных событий записывается в виде:

Сначала найдем вероятности событий A и B. Так как всего участников  и из них  из Италии, то

Теперь вычислим вероятность произведения событий A и B. Видим, что эти события зависимы, так как при возникновении события A (первым участвует пловец из Италии), остается меньше на одного пловца и на одного спортсмена из Италии. Поэтому,

где . Соответственно,

Подставляем все числовые значения в формулу суммы, получаем искомую вероятность:

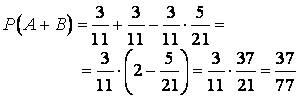
Ответ: 37/77.

 

Задача 3. Помещение освещается фонарем с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,2. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.

Решение.

А) Через умножение событий. Обычно такие задачи решают с использованием противоположных событий. Сначала определяются два независимых события:

A: в течение года перегорит первая лампа;

B: в течение года перегорит вторая лампа.

Затем, вычисляется вероятность того, что и первая и вторая лампы перегорят, то есть, вычисляется вероятность произведения событий :

И, так как, по условию задачи , получаем:

.

Противоположное событие  будет означать «не перегорание хотя бы одной лампы». Вероятность этого события, равна:

Б) Через сложение событий. Эту же задачу можно решить и через сложение событий. Введем два события:

A: в течение года не перегорит первая лампа;

B: в течение года не перегорит вторая лампа.

Фраза «хотя бы одна лампа не перегорит» означает, что не перегорит первая лампа или не перегорит вторая лампа. То есть, нужно найти вероятность суммы событий . Очевидно, что эти события совместны – они могут произойти одновременно (в пределах года), следовательно,

Вероятности событий , а вероятность их произведения, равна

,

так как эти события независимы. Подставляем числовые значения в формулу, получаем:

Ответ: 0,96.

 

Задача 4. По отзывам покупателей Михаил Михайлович оценил надежность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,61. Вероятность того, что этот товар доставят из магазина Б, равна 0,83. Михаил Михайлович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что хотя бы один магазин доставит товар.

 

 

 

 

 

 

·       юВ торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

решение

В конце дня могло возникнуть четыре различных ситуации:

·         кофе остался в обоих автоматах (+,+) ;

·         кофе закончился только в первом автомате (-,+) ;

·         кофе закончился только во втором автомате (+,-) ;

·         кофе закончился в обоих автоматах (-,-).

Это и есть ни что иное, как наши четыре элементарных исхода. По условию для каждого автомата по отдельности вероятность того, что в нем закончится кофе, равна 0,3. Значит, событию «кофе закончилось в первом автомате», которое состоит из элементарных исходов (-,-), (-,+) соответствует вероятность 0,3. Событию «кофе закончится в обоих автоматах» соответствует ровно один элементарный исход (-,-).  Тогда

По аналогичным соображениям

Теперь легко найти вероятность интересующего нас элементарного исхода «кофе остался в обоих автоматах  1-0,18-0,18-0,12=0,52

Ответ: 0,52

 

·       Гигрометр измеряет влажность в помещении картинной галереи. Вероятность того, что влажность окажется выше 40%, равна 0,82. Вероятность того, что влажность окажется ниже 56%, равна 0,74. Найдите вероятность того, что влажность находится в пределах от 40% до 56%.

решение

Ответ: 0,56

 

·       Ваня бьет по мячу. Рядом стоит 10-этажный дом. Вероятность события “Ваня выбил окно на этаже, номер которого четный” равна 0,01. Вероятность события “Ваня выбил окно на этаже, номер которого делится на 3” равна 0,02. Вероятность того, что Ваня выбьет окно на 6 этаже, равна 0,05. Какова вероятность того, что окна на четных этажах, как и окна на этажах с номерами, кратными 3, не пострадают?

решение

Найдем вероятность того, что пострадает окно на четном этаже или пострадает окно на этаже, номер которого делится на 3.

Вероятность наступления по крайней мере одного из двух событий равна сумме вероятностей этих событий минус вероятность их одновременного наступления, тогда вероятность того, что пострадает окно одного из оговоренных этажей

Следовательно, вероятность того, что окна на четных этажах, как и окна на этажах с номерами, кратными 3, не пострадают, равна 

Ответ: 0,975

 

·     В классе учится 20 человек, из которых 4 занимаются плаванием, 5 занимаются шахматами. Известно, что и плаванием, и шахматами занимаются 2 ученика этого класса. Какова вероятность того, что выбранный наугад ученик этого класса занимается по крайней мере одним из этих видов спорта?

 

·     Среди десяти котят в коробке четверо мужского пола, у троих кончик хвоста белый. Известно, что ровно у 2 котят мужского пола кончик хвоста не белый. Таня выбирает себе одного котенка наугад. Какова вероятность того, что выбранный котенок будет мужского пола или с белым кончиком хвоста, или и то и другое?

решение

Среди котят мужского пола в коробке у4-2=2 кончик хвоста белый. Вероятность наступления по крайней мере одного из двух событий равна сумме вероятностей этих событий минус вероятность их одновременного наступления, тогда искомая вероятность равна 

Ответ: 0,5

 

·       В аквариуме плавает 100 рыбок. Известно, что из них 17 золотых, 4 исполняют желания. При этом золотых рыбок,  которые исполняют желания в аквариуме 3. Покупатель хочет приобрести золотую рыбку, которая исполняет желания (как в сказке). Найдите вероятность того, что выбранная наугад рыбка будет соответствовать хотя бы одному требованию покупателя.

решение

Вероятность наступления по крайней мере одного из двух событий равна сумме вероятностей этих событий минус вероятность их одновременного наступления, тогда искомая вероятность равна 

Ответ: 0,18

 

·     Максик и Леша ждут Деда Мороза с подарками на Новый год. Вероятность того, что Леша угадает, какой подарок он получит от Деда Мороза, равна 0,95. Вероятность того, что Максик угадает, какой подарок он получит от Деда Мороза, равна 0,9. Вероятность обоим братьям угадать подарки от Деда Мороза равна 0,88. Какова вероятность того, что братьям не повезет и они не угадают, что получат на Новый год от Деда Мороза?

решение

Найдем вероятность того, что по крайней мере один из двух братьев угадает, что ему подарит на Новый год Дед Мороз. Вероятность наступления по крайней мере одного из двух событий равна сумме вероятностей этих событий минус вероятность их одновременного наступления, следовательно, вероятность искомого события равна

Следовательно, вероятность того, что ни один из братьев не угадает свой подарок на Новый год, равна 1-0,97=0,03

Ответ: 0,03

·       Лампочка в левой комнате некоторого блока в общежитии перегорает в среднем 1 раз в 20 включений. Лампочка в правой комнате этого блока перегорает в среднем 1 раз в 50 включений. Вероятность того, что при одновременном включении лампочек обе перегорят, составляет 0,01. Какова вероятность того, что при одновременном включении ни одна из лампочек не перегорит?

решение

Найдем вероятность того, что при одновременном включении хотя бы одна из этих лампочек перегорит.

Вероятность наступления по крайней мере одного из двух событий равна сумме вероятностей этих событий минус вероятность их одновременного наступления. Тогда вероятность того, что перегорит хотя бы одна лампочка, равна

Следовательно, вероятность того, что не перегорит ни одна лампочка, равна 1-0,06=0,94

Ответ: 0,94

 

·       Вероятность того, что маленький Миша заплачет, увидев в зоопарке медведя, составляет 0,3. Вероятность того, что маленькая Маша заплачет, увидев в зоопарке медведя, составляет 0,4. Вероятность того, что Миша и Маша вместе заплачут, увидев в зоопарке медведя, составляет 0,15. Какова вероятность того, что по крайней мере один из них заплачет, увидев в зоопарке медведя?

решение

Событие «Маша или Миша заплачет» складывается из следующих элементарных событий.

Событие «Миша заплачет и Маша не заплачет» с вероятностью  0,3-0.15

Событие «Миша не заплачет и Маша заплачет» с вероятностью 0,4-0,15

Событие «Миша заплачет и Маша заплачет» с вероятностью 0,15.

Тогда искомая вероятность равна

р= (0,3-0.15)+( 0,4-0.15)+0,15=0,55

 

Ответ: 0,55

 

(А) Маршрутный лист (Ф.И.)_____________________________________________

 

П/д	Задания	Контроль и результат	Критерии оценки	Оценка
1	Выполнить проверочный тест	Выполненный тест, соответствие с эталоном ответов,	Менее 6 правильных ответов – «2», 6,7 правильных ответов - «3», 8,9 правильных ответов – «4», 10 правильных ответов - «5»
2	Определение темы, целей и задач занятия	Запись в тетради, озвучивание, соответствие
3	Работа с э/модулем	Освоение модулей М1, М2: выполнение заданий для самоконтроля	Менее 2 правильно выполненных заданий - «2», правильно 2 задания – «3», правильно 3 заданий – «4», правильно 4 заданий- «5»
4	Работа с информационным текстом	Составление опорного конспекта	Оценка преподавателя
5	Решение задач	Устные ответы, запись в тетрадь	Оценка преподавателя
6	Написание синквейна	Запись в тетради, озвучивание
9	Подведение итогов	Оценка за занятие

Лист 2.

Проверочный тест

Вариант 1.

№ 1. Выбери правильный ответ.

Число характеризующее возможность наступления события- это…

а) размещение, б) сочетание, в) перестановка, г) вероятность

№ 2.Сопоставьте названия элементов комбинаторики с формулами

 

№ 3 Вычислите:

№ 4. Выберите из высказываний – испытания:

а) сдача экзамена; б) получение определенной отметки, в) выстрел;

г) попадание в определенную область мишени, д) бросание игрального кубика; е) появление того или иного числа очков на брошенной игральной кости, ж) ремонт автомобилей, з) устранение неисправности автомобиля.

№ 5.Выберите правильный ответ.

Укажите вид данных событий: идет дождь и идет снег, человек ест и человек читает, число целое и четное.

а) несовместные события; б) совместные события

№ 6. К какому событию относится данная формула вероятности: Р(А) = 1.

а) Вероятность случайного события А

б). Вероятность невозможного события А

в) Вероятность достоверного события А

№ 7. Сдаче экзамена по дисциплине возможны четыре варианта: оценка  «2», «3», «4», «5» (n=4). Нас интересует оценка «5» (m=1). С точки зрения теории вероятности  вероятность её получения равна p= и не зависит от того, что будет студент готовиться или нет. В чем ошибка этого рассуждения:

а) Экзаменационная оценка определяется уровнем знания студента, а не является случайной.

б) Рассмотренные события не являются совместными, поэтому эту формулу использовать нельзя.

в) Рассмотренные события не являются равновозможными, поэтому эту формулу использовать нельзя.

г) Рассмотренные события не образуют полную группу, поэтому эту формулу использовать нельзя.

№ 8.В сервисном центре по техническому обслуживанию автомобилей находятся 10 заявок. Сколькими способами можно распределить эти заявки, если в день ремонтировать по 4 автомобиля.

а) 24, б) 10!, в) 120, г) 210

№ 9. На автогонках при заезде на первой автомашине вероятность победить Р₁=0,6, при заезде на второй автомашине Р₂=0,9. Найти: вероятность того, что победят обе автомашины

№10. При встрече каждый из друзей пожал другому руку. Сколько всего было рукопожатий, если встретились 6 друзей?

Проверочный тест

Вариант 2.

№ 1. Выбери правильный ответ.

Любой исход опыта, который может произойти или не произойти называется …

а) вероятность, б) комбинаторика, в) событие, г) случайная величина

№ 2. Сопоставьте буквенное обозначение элементов комбинаторики с формулами

№ 3.Вычислите:

№ 4. Выберите из высказываний – событие:

а) сдача экзамена; б) получение определенной отметки, в) выстрел;

г) попадание в определенную область мишени, д) бросание игрального кубика; е) появление того или иного числа очков на брошенной игральной кости, ж) ремонт автомобилей, з) устранение неисправности автомобиля.

№ 5.Выберите правильный ответ. Укажите вид данных событий: день и ночь, человек читает и человек спит, число иррациональное и четное

а) несовместные события; б) совместные события

№ 6. К какому событию относится данная формула вероятности: Р(А) = 0.

а) Вероятность достоверного события А

б). Вероятность невозможного события А

в) Вероятность случайного события А

№ 7. Ремонт автомобиля на станции тех. Обслуживания выполняется до 4 рабочих дней. Клиенту сказали, что вероятность получения автомобиля в последний день будет равна 0,1. Клиент уверено заявил членам семьи что автомобиль будет в их расположении к вечеру завтрашнего дня. Недоумение своих близких он объяснил следующим расчетом: р=1-0,1= 0,9. В чем ошибка клиента:

а) Данная формула справедлива для элементарных событий, а получения автомобиля в первый и последний день события не элементарные.

б) Теория вероятностей не применима для ремонта автомобилей.

в) Данная формула справедлива для противоположных событий, а событие в первый и последний день события не противоположные.

г) Данная формула справедлива для совместных событий, а событие в первый и последний день события не совместные.

№ 8. В группе 24 студента. На устный экзамен в первый заход приглашаются по 5 человек. Сколькими способами можно составить график первой пятерки.

а) 24!, б) 120, в) 42504, г) 20*21*22*23*24

№ 9. На автогонках при заезде на первой автомашине вероятность победить Р₁=0,6, при заезде на второй автомашине Р₂=0,9. Найти: вероятность того, что победит хотя бы одна автомашина.

№10. При окончании деловой встречи специалисты обменялись визитными карточками. Сколько всего визитных карточек перешло из рук в руки, если во встрече участвовали 6 специалистов?

 

Лист 3.

 

Ответы к проверочному тесту.

1 вариант:

1	2	3	4	5	6	7	8	9	10
г	231	48	а,в,д,ж	б	в	в	210	0,54	15

 

2 вариант:

1	2	3	4	5	6	7	8	9	10
в	231	78	б,г,е,з	а	б	в	42504	0,96	30

 

Лист 4.

Информационный текст

"Статистика знает всё" известно, сколько какой пищи съедает в год средний гражданин республики: известно, сколько в стране охотников, балерин, станков, велосипедов, памятников, маяков и швейных машинок. Как много жизни, полной пыла, страстей и мысли, глядит на нас со статистических таблиц!..".Это ироничное описание даёт общее представление о статистике (отрывок из романа Ильфа и Петрова "Двенадцать стульев")

Сегодня мы познакомимся с новой наукой – статистикой. Узнаем, что она изучает и как можно применить те знания, которые вы сейчас получите. Термин "статистика" произошел от латинского слова "статус" (status), что означает "состояние и положение вещей.

Возникновение статистики было связано с потребностями государственного управления. Уже ранние государства - Китай, Египет, Древняя Греция - нуждались в данных о населении и его составе, имущественном положении граждан, количестве скота, земельных угодий и т.д., положивших начало статистической практике.

Статистика как наука стала развиваться со второй половины ХVII в., когда в Европе сложились две основные школы: в Англии - математическая школа статистики, в Германии - описательная школа статистики. Ярким представителем первой школы был Уильям Петти (1623 - 1687), который по праву считается основоположником статистической науки. Он впервые широко применил математику для экономического анализа.

Известными представителями описательной школы статистики были немецкие ученые Генрих Конринг (1606 - 1681) и Генрих Ахенваль (1719 - 1772). Основной целью статистики они считали описание политического состояния и достопримечательностей государства, где числовые характеристики были лишь частью предмета статистики.

Статистика изучает: численность отдельных групп населения страны и ее регионов, производство и потребление разнообразных видов продукции, перевозку грузов и пассажиров различными видами транспорта,  природные ресурсы и многое другое. Результаты статистических исследований широко используются для практических и научных выводов.

Жизнедеятельность общества свидетельствует о востребованности статистики, не только как надёжного первоисточника данных, но и мощного инструмента познания объективных закономерностей прошлого и будущего развития окружающего мира.

С помощью статистических методов можно доказать экономические предположения, проверить теоретические гипотезы, восстановить и пополнить существующие оценки, а также представить изучаемые явления в полном объёме накопленных знаний. Нет другой отрасли современных знаний, которая решала бы эти вопросы более квалифицированно.

Что такое статистика? Это наука, изучающая количественные показатели развития общества и общественного производства. Роль статистики в нашей жизни настолько значительна, что люди, часто не задумываясь и не осознавая, постоянно используют элементы статистической методологии не только в трудовых процессах, но и в повседневном быту. Работая и отдыхая, делая покупки, знакомясь с другими людьми, принимая какие-то решения, человек пользуется определённой системой имеющихся у него сведений, сложившихся вкусов и привычек, фактов, систематизирует, сопоставляет эти факты, анализирует их, делает выводы и принимает определённые решения, предпринимает конкретные действия. Таким образом, в каждом человеке заложены элементы статистического мышления, представляющего собой способности к анализу и синтезу информации об окружающем нас мире.

Можно без преувеличения сказать, что статистическими методами сегодня пронизана вся наша жизнь. Как только человеку в его деятельности потребовались количественные характеристики, то есть числа, тут же появилась статистика. Конечно, она не называлась так, но самые первые статистические исследования можно обнаружить и в древних египетских папирусах, и на вавилонских глиняных табличках. Отсутствие строгой, научной базы статистических прогнозов, произвольное толкование статистических данных позволили в конце XIX века английскому премьер - министру Б.Дизраэли заметить: "Есть три вида лжи. Просто ложь, наглая ложь и статистика".

В XX веке появилась математическая статистика, обладающая универсальными методами сбора, хранения и обработки информации для выработки различных прогнозов, оценка их достоверности - основные задачи статистики.

Профессии, связанные со статистикой. Существует множество профессий различного типа. Это профессии типа:

«Человек – человек» (врач, учитель, психолог)

«Человек – техника» (столяр, металлург, инженер - механник)

«Человек – природа» (семеновод, зоотехник, агроном)

«Человек – художественный образ» (артист, музыкант, дизайнер)

«Человек – знаковые системы»

Остановимся подробнее именно на этом типе профессий. Здесь главный, ведущий предмет труда – условные знаки, цифры, коды, естественные или искусственные языки. Современный человек погружен в мир знаков и знаковых систем: чертежи, схемы, карты, численные данные, таблицы, формулы – всё это неотъемлемые черты проявления современной цивилизации. Значит, нужны и соответствующие специалисты, работающие со знаковыми системами, готовят и хранят информацию, анализируют её, создают теоретические основы для усовершенствования машин, механизмов, создают электронно - вычислительную технику.

С абстрактно - математическими системами работают математики, астрономы, химики, которые создают информацию. Накапливают, анализируют и обрабатывают информацию: учётчики, бухгалтеры, лаборанты, статисты. Сегодня, для того чтобы быть конкурентоспособным на рынке труда, экономисту, финансисту, менеджеру необходимо владеть статистическими методами сбора, обработки и анализа данных.

Статистическая информация - это числовые данные о массовых явлениях. Без минимальной вероятностно-статистической грамотности трудно воспринимать социальную, политическую, экономическую информацию и принимать на ее основе обоснованные решения.

Современные физика, химия, биология, весь комплекс социально-экономических наук построен и развиваются на вероятностно-статистической базе. Без знания понятий и методов теории вероятностей и статистики невозможна организация эффективного конкурентоспособного производства, внедрение новых лекарств и методов лечения в медицине.

Элементы математической статистики. При проведении статистического исследования после сбора и группировки данных переходят к их анализу, используя для этого различные обобщающие показатели. Простейшими из них являются числовой ряд- представление данных, частота (абсолютная) показывает сколько раз встречается каждое значение, относительная частота-отношение  абсолютной частоты к общему количеству данных, среднее арифметическое ряда чисел - это отношение суммы чисел на количество  данных, размах ряда – разность между наибольшим и наименьшим  из ряда чисел, мода – число, часто встречающееся в данном ряду, медианой ряда состоящего из нечетного количества чисел, называется число данного ряда, которое окажется посередине, если ряд упорядочить. Если в ряду четное число данных , то тогда медиана- это среднее арифметическое двух стоящих посередине чисел данного ряда.

В процессе собирания фактов о изученном массовом явлении (статистическом наблюдении), а затем и на следующих стадиях статистического исследования (в процессе группировки, сводки, анализа) встает вопрос о способе представления и записи результата  данных. Изложить в форме текста большой цифровой материал (статистическое исследование) трудно.

Для геометрического изображения такого статистического распределения служит полигон частот (рис.1.1) или гистограмма, диаграмма. Полигоном частот называют ломаную линию, отрезки, которой соединяют точки. Для построения полигона частот на оси абсцисс откладывают варианты, а на оси ординат – соответствующие им частот. Статистическое распределение можно задать также в виде последовательных интервалов и соответствующих частот. Статистический ряд в таком случае называется интервальным  статистическим рядом. Такое изображение  называется гистограммой.(рис 1.2)- ступенчатая фигура в виде прямоугольников.

           

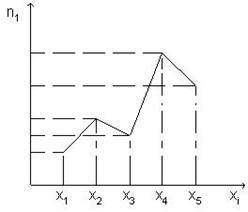
Рис.1.1 Полигон частот                     Рис.1.2.Гистограмма частот

 

Лист 5.

Задачи для фронтальной работы

Задание №1

Определить какая статистическая характеристика находится в каждом задании:

а) 100+75+50+75=300; 300:4=75; 75-………………………………………

б) 50, 75, 75, 100; (75+75):2 = 75; 75-…………………………………….

в) 100, 75, 50, 75; 75- ………………………………………………………

г) 100 - 50=50; 50- …………………………………………………………

д) 100, 75, 50, 75; 75-2 раза-………………………………………………

Задание №2

В колледже группа студентов сдавали экзамен по математике, и они получили соответствующие оценки:

3, 5, 5, 4, 4, 4, 3, 2, 4, 5.

Ответьте на следующие вопросы, и какие статистические характеристики дают ответ на поставленный вопрос:

Сколько в группе человек?

Какую оценку получали чаще всего?

Как в целом сдала группа?

Насколько разные были оценки?

Задание№3

Найдите среднее арифметическое ряда чисел

23, 18, 25, 20, 25, 25, 32, 37, 34, 26, 34, 25

Задача №4:

Найти среднее арифметическое, размах, моду и медиану ряда чисел:

а) 20, 18, 32, 10, 45, 15, 18, 12

б) 2, 2;3, 8;1, 6;4, 4;1, 5.

Задача 5.

В организации вели ежедневный учет поступивших в течение месяца писем. В результате получили такой ряд данных:

39, 43, 40, 0, 56, 38, 24, 21, 35, 38, 0, 58, 31, 49, 38, 45, 34, 0, 32, 40, 40, 42, 39, 54, 0, 64, 44, 50, 38, 37, 32.

Для полученного ряда найдите частоту, среднее арифметическое, размах, моду и медиану. Каков практический смысл этих показателей?

 

Ответы:

№ 1. а) среднее арифметическое, б) медиана, в) мода, г) размах, д) абсолютная частота

№ 2.объем (ряд) данных, мода, среднее арифметическое, размах

№ 3.27

№ 4. а) среднее арифметическое – 21, 25; размах – 35; мода – 18; медиана - 18;

б) среднее арифметическое – 2, 7; размах – 2, 9; мода – нет; медиана – 2, 2.

№ 5.частота – 4 - самое большое число писем было 4; среднее арифметическое - 31,2 – в среднем за месяц пришло 31 письмо в день;, размах – 64 – на сколько разное было количество писем в день за месяц;, мода - 0 и 38 – чаще всего не было писем или их было 38; медиана – 40 - в середине месяца пришло в день 40 писем.

Лист 6.

Составить синквейн и в поэтической форме выразить свое отношение к изученному материалу: структура синквейна

1.       Существительное - термин

2.       Два прилагательных

3.       Три глагола

4.       Личное отношение, собственное мнение

5.       Синоним к термину

 

 

Лист 7.

 

Опорный конспект

Тема:

Цель занятия:

Происхождение терминов:

История возникновения науки (время, место, ученые):

 

Интересные факты:

 

Статистические характеристики

(термин, обозначение, формула или правила вычисления, практическое значение)

 

 

 

 

 

Лист 8.

Скачано с www.znanio.ru