Учебно-методическое пособие по теме «ЛОГАРИФМЫ» предназначено для организации аудиторной и самостоятельной работы обучающихся 1 курса средних профессиональных учебных заведений, осуществляющих обучение на базе основного общего образования.В пособии содержится большое количество практических заданий. Предложенные задания закрепляют полученные обучающимися теоретические знания по теме: «Логарифмы», позволяют им освоить навыки решения разбора различных логарифмических выражений с подробным изучением основных формул, а так же изучить различные методы решения логарифмических уравнений, применяемые в каждом конкретном случае.

Севастопольское государственное бюджетное образовательное учреждение

профессионального образования

«Севастопольский медицинский колледж имени Жени Дерюгиной»

СОГЛАСОВАНО

протокол МЦК

от ______________2024 г. №

Председатель ЦМК

______________Смирнова З. М.

УТВЕРЖДАЮ

Зам. директора по учебной работе

________________Полстянко Н.Н.

«_____» _______________ 2024 г.

Методическая разработка

практического занятия

Тема ”Логарифм числа и его свойства ”

ОУД 07. Математика

для специальности 34.02.01 «Сестринское дело»

31.02.01 «Лечебное дело»

курс I (база ООО)

Автор Тищенко Е.Ю

Севастополь 2024 г.

тема: « ЛОГАРИФМЫ »

Дисциплина: «МАТЕМАТИКА»

Аннотация:

В пособии содержится большое количество практических заданий. Предложенные задания закрепляют полученные обучающимися теоретические знания по теме: «Логарифмы», позволяют им освоить навыки решения разбора различных логарифмических выражений с подробным изучением основных формул, а так же изучить различные методы решения логарифмических уравнений, применяемые в каждом конкретном случае.

Оглавление

Пояснительная записка. 4

Откуда взялся Log?. 7

Свойства логарифмов. 9

Дифференцированный набор заданий по теме «Понятие логарифма». 11

Свойства логарифмов (образцы решения) 14

Набор заданий для систематизации знаний. 22

Дифференцированный набор заданий для систематизации знаний «Свойства логарифма». 28

Основные типы логарифмических уравнений. 31

Образцы решения логарифмических уравнений. 33

Тест по теме «Логарифмические уравнения». 41

Набор заданий для систематизации знаний для решения логарифмических уравнений 45

Лист контроля по теме: «Логарифмическая функция». 47

Количество вариантов: 48

Заключение. 49

Приложение. 51

«Изобретение логарифмов, сократив работу астронома, продлило ему жизнь»

П.С.Лаплас

Пояснительная записка

Учебно-методическое пособие по теме «ЛОГАРИФМЫ» предназначено для преподавателей математики и обучающихся 1 курса средних профессиональных учебных заведений, осуществляющих обучение на базе основного общего образования. Пособие предназначено для реализации государственных требований к минимуму содержания и уровню подготовки студентов по дисциплине «Математика».

Учебно–методическое пособие создано в связи с недостаточным количеством раздаточного материала, применяемого при изучении темы: «Логарифмы».

Пособие интересно тем, что для изучения, закрепления, а так же контроля разработаны и подобраны материалы разных видов.

Данное методическое пособие поможет студентам при изучении логарифмов. В пособии приводятся определение логарифма, свойства, основные формулы, а также примеры решения логарифмов, логарифмических выражений.

Работая с данным пособием, студенты будут четко знать основные способы решения логарифмов и логарифмических выражений, уметь быстро определять нужную формулу.

Данное методическое пособие могут использовать в своей работе и преподаватели с целью организации аудиторной и самостоятельной работы :

· систематизации, закрепления и углубления полученных теоретических и практических знаний, умений;

· формирования умений применять теоретические знания;

· развития самостоятельности и организованности студентов;

Использование пособия на различных этапах занятия предполагает экономию времени и усилий (преподавателя, студента) за счет компактного изложения теоретического материала; иллюстрации каждой формулы примерами; подробно разобранных заданий; упражнений подобранных в системе.

Учебно - методическое пособие позволит студентам с наибольшей эффективностью организовать свою деятельность по подготовке к успешной сдаче экзамена.

Оценка качества выполнения студентами заданий будет осуществляться поэтапно, в соответствии с планом занятий по пятибалльной шкале.

Критерии оценок:

Отметка «5» ставится, если:

· работа выполнена полностью;

· в логических рассуждениях и обосновании решения нет пробелов и ошибок;

· в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).

Отметка «4» ставится, если:

· работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

· допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки).

Отметка «3» ставится, если:

· допущены более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но учащийся владеет обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

· допущены существенные ошибки, показавшие, что учащийся не владеет обязательными умениями по данной теме в полной мере.

Отметка «1» ставится, если:

· работа показала полное отсутствие у учащегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.

Откуда взялся Log?

Мы изучили показательные уравнения. Давайте повторим, решив одно из них.

= 32. (1)

Запишем данное уравнение так: =, откуда х = 5.

Напомним, что левую и правую части уравнения удалось представить в виде степени с одним и тем же основанием 2.

А теперь, попробуем решить еще одно показательное уравнение. = 30. (2)

Теперь, тех знаний с точки зрения решения показательных уравнений, недостаточно.

Есть ли корень у этого показательного уравнения? Да, есть.

Как его найти, если уравнение не решается привычным способом?

И теперь, мы введем понятие «логарифм», которое поможет нам решить данное уравнение.

Важно запомнить!

Логарифм (от греч. λόγος – «слово», «отношение», άριθμός - «число») определяется как показатель степени, в которую надо возвести основание, чтобы получить число.

Для начала, представим наши показательные уравнения в виде стандартной формы (т.е. заменим числа с правой и левой стороны на а и b),

напишем: = b.

Важно запомнить!

Корень х уравнения = b будем находить так:

х =b, где а >0, а1, b >0.

Соотнесем теперь определение логарифма с (1) показательным уравнением:

= 32 х =32

х = 5, так как = 32

Значит, 32 = 5, так как = 32.

Мы решили показательное уравнение с помощью применение логарифма.

Теперь, представим (2) показательное уравнение в виде логарифма и попробуем решить его: = 30 х =30.

х =30 – это и есть корень уравнения = 30. На инженерном калькуляторе это будет приблизительно.

Так откуда же взялся логарифм? А он взялся из-за потребности решить показательное уравнение, которое не решается привычным способом.

Свойства логарифмов

ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ ЛОГАРИФМИЧЕСКИХ И ПОКАЗАТЕЛЬНЫХ ВЫРАЖЕНИЙ

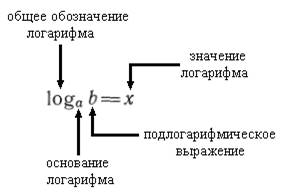
Логарифмом числа b по основанию а называется показатель степени, в которую надо возвести число а, чтобы получилось b:

Основное логарифмическое тождество

Общая схема вычисления логарифмов. Она состоит из трех шагов: Ø Представить основание и аргумент в виде степени с минимально возможным основанием, большим единицы. Попутно лучше избавиться от десятичных дробей; Ø Решить относительно переменной уравнение: Ø Полученное число будет ответом.
	Задача Вычислите логарифм: Решение: Представим основание и аргумент как степень двойки Составим и решим уравнение: Ответ:	Задача Вычислите логарифм: Решение: Представим основание и аргумент как степень тройки: Составим и решим уравнение: Ответ:
	Задача Вычислите логарифм: Решение: Представим основание и аргумент как степень двойки Составим и решим уравнение: Ответ:	Задача Вычислите логарифм: Решение: Представим основание и аргумент как степень пятерки: Составим и решим уравнение: Ответ:
	Задача Вычислите логарифм: Решение: Представим основание и аргумент как степень семерки: в виде степени семерки не представляется, поскольку следует, что логарифм не считается. Ответ:

Дифференцированный набор заданий по теме «Понятие логарифма»

1 вариант	2 вариант	3 вариант
Вычислить:	Вычислить:	Вычислить:
1. 16	1. 128	1. 64
2. 2	2. 1	2. 4
3. 27	3. 9	3. 81
4. 1	4. 3	4. 243
5. 25	5. 625	5. 216
6. 1	6. 15	6. 16
7. 121	7. 1	7. 7
8. 4096	8. 512	8. 64
9. 729	9. 729	9. 81
10. 36	10. 49	10. 25

1 вариант	2 вариант	3 вариант
Вычислить:	Вычислить:	Вычислить:
1.	1.	1.
2.	2.	2.
3.	3.	3.
4.	4.	4.
5. 2	5. 2	5. 2
6. 27	6. 9	6. 81
7.	7.	7.
8. 0,125	8. 0,5	8. 32
9. 225	9.	9.
10. 1	10.	10. 0,1

1 вариант	2 вариант	3 вариант
Вычислить:	Вычислить:	Вычислить:
1.	1.	1.
2.	2.	2.
3.	3.	3.
4.	4.	4.
5. 15	5.	5. 15
6. 81	6. 9	6. 81
7.	7.	7.
8. 49	8.	8.
9.	9.	9.
10.	10.	10.

Свойства логарифмов (образцы решения)

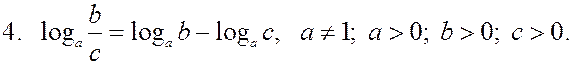
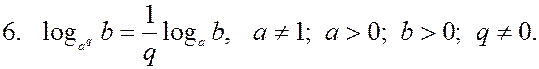
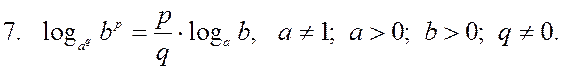
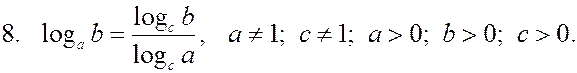
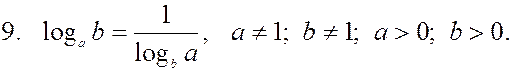
Другие виды обозначения логарифмов:

логарифм числа b по основанию e

(натуральный логарифм)

e = 2,718281828459045… – основание натурального логарифма;

логарифм числа b по основанию 10

(десятичный логарифм)

10 – основание десятичного логарифма.

Логарифмическая единица

и логарифмический ноль

— это логарифмическая единица.

Запомните раз и навсегда:

логарифм по любому основанию от самого этого основания равен единице.

Например: .

— это логарифмический ноль.

Основание может быть каким угодно, но если в аргументе стоит единица — логарифм равен нулю! Потому, что — это прямое следствие из определения.

Например: .

Сложение и вычитание логарифмов
Итак, сумма логарифмов равна логарифму произведения, а разность — логарифму частного. Обратите внимание: ключевой момент здесь — одинаковые основания. Если основания разные, эти правила не работают.

Задача Представьте логарифм в виде суммы: Решение: Представим число 14 в виде произведения и применим формулу суммы: Ответ:	Задача Найдите значение выражения: Решение: Поскольку основания у логарифмов одинаковые, используем формулу суммы: Ответ:

Задача Представьте логарифм в виде разности: Решение: Представим число 0,4 в виде обыкновенной дроби и применим формулу разности: Ответ:	Задача Найдите значение выражения: Решение: Поскольку основания у логарифмов одинаковые, используем формулу разности: Ответ:

Вынесение показателя степени из логарифма

Задача

Найдите значение выражения:

Решение:

Избавимся от степени в аргументе по пятой формуле:

Ответ:

Задача

Найдите значение выражения:

Решение:

Избавимся от степени в основании по шестой формуле:

Ответ:

Задача

Найдите значение выражения:

Решение:

Избавимся от степени в аргументе и основании по седьмой формуле:
Ответ:

Задача

Найдите значение выражения:

Решение:

Избавимся от степени в аргументе по пятой формуле:

Ответ:

Задача

Найдите значение выражения:

Решение:

Заметим, что в знаменателе стоит логарифм, основание и аргумент которого являются точными степенями: Имеем:

Ответ:

Задача

Найдите значение выражения:

Решение:

Избавимся от степени в аргументе по пятой формуле:

Ответ:

Задача

Найдите значение выражения:

Решение:

Заметим, что в знаменателе стоит логарифм, основание и аргумент которого являются точными степенями: Имеем:

Ответ:

Переход к новому основанию

Из девятой формулы следует, что можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе.

Задача

Представьте в виде логарифма с основанием 2.

Решение:

Воспользуемся восьмой формулой:

Ответ:

Задача

Представьте в виде логарифма с основанием 7.

Решение:

Воспользуемся девятой формулой:

Ответ:

Задача Найдите значение выражения: Решение: Заметим, что в аргументах обоих логарифмов стоят точные степени. Вынесем показатели: А теперь «перевернем» второй логарифм: Поскольку от перестановки множителей произведение не меняется, мы спокойно перемножили четверку и двойку, а затем разобрались с логарифмами. Ответ:
Задача Найдите значение выражения: Решение: Основание и аргумент первого логарифма — точные степени. Запишем это и избавимся от показателей: Теперь избавимся от десятичного логарифма, перейдя к новому основанию: Ответ:
Основное логарифмическое тождество
Часто в процессе решения требуется представить число как логарифм по заданному основанию. В этом случае нам помогут формулы:

В первом случае число n становится показателем степени, стоящей в аргументе. Число n может быть абсолютно любым, ведь это просто значение логарифма	Вторая формула — это фактически перефразированное определение. Она так и называется: основное логарифмическое тождество
Задача Найдите значение выражения: Решение: Применяя основное логарифмическое тождество, получаем: Ответ:
Задача Найдите значение выражения: Решение: Заметим, что — просто вынесли квадрат из основания и аргумента логарифма. Учитывая правила умножения степеней с одинаковым основанием, получаем: Ответ:

Набор заданий для систематизации знаний

Вычислите:

Перейдите к логарифмам:

61) с основанием 3

62) с основанием 10

63) с основанием π

64) с основанием a+b

65) с основанием

Вычислите:

Представьте выражение в виде логарифма:

66)

67)

68)

69)

70)

Представьте 1 в виде логарифма:

6) с основанием 4

7) с основанием 10

8) с основанием e

9) с основанием -3

10) с основанием 5

Поменяйте местами основание и подлогарифмическое выражение так, чтобы значение выражения не изменилось:

71)

72)

73)

74)

75)

Вычислите:

11)

12)

13)

14)

15)

Замените выражение логарифмом:

76)

77)

78)

79)

80)

Представьте 0 в виде логарифма:

16) с основанием 4

17) с основанием 10

18) с основанием e

19) с основанием

20) с основанием 5

Представьте логарифм произведения в виде суммы логарифмов:

21)

22)

23)

24)

25)

Представьте сумму логарифмов в виде логарифма произведения:

26)

27)

28)

29)

30)

Вычислите:

81)

82)

83)

84)

85)

86)

87)

Представьте логарифм частного (дроби) в виде разности логарифмов:

31)

32)

33)

34)

35)

Вычислите:

88)

89)

90)

91)

Представьте разность логарифмов в виде логарифма частного (дроби):

36)

37)

38)

39)

40)

Зная, что lga = x и lgb = y, найдите десятичные логарифмы выражений:

92) ab

93)

94) a³

95) a³b³

96) a⁵b⁴

97)

98)

99)

Упростите выражение:

41)

42)

43)

44)

45)

Вычислите:

100)

101)

102)

103)

Представьте выражение в виде логарифма степени:

46) 2log₂a

47) log₂b

48) 2ln

49) 3log11

50) mlg3

Прологарифмируйте по основанию 10

(a> 0, b> 0, c> 0, a>b):

104) 3ab

105)

106)

107) 2(a + b)

108)

109) 100( a – b)²

Упростите выражение:

51)

52)

53)

54)

55)

Найдите значения выражений:

110)

111)

112)

113)

114)

115)

116)

Удалите множитель перед знаком логарифма, преобразовав основание логарифма:

56)

57)

58)

59)

60)

ТЕМА: ЛОГАРИФМЫ Задание: вычислите

Допишите формулы, если это возможно.	1)	= где х; у>0
	2)	= где х; у>0
	3)	=
	4)	=
	5)	=
	6)	=
	7)	= где n - нечетно
	8)	= где n - четно
	9)	=
	10)	=
	11)	=
	12)	=
	13)	=
	14)	=
	15)	=
	16)	= где х; у>0
	17)	= где х; у>0
	18)	=
	19)	Замените логарифмом
	20)	=
	21)	=

ТЕМА: ЛОГАРИФМЫ Задание: вычислите
1.	2.	3.
4.	5.	6.
7.	8.	9.
10.	11.	12.
13.	14.	15.
16.	17.	18.
19.	20.	21.
22.	23.	24.
25.	26.	27.
28.	29.	30.
31.	32.	33.
34.	35.	36.
37.	38.	39.
40.	41.	42.
43.	44.	45.

Дифференцированный набор заданий для систематизации знаний «Свойства логарифма»

Вариант – 1

Вариант – 2

Вариант – 3

Вариант –4

1. Вычислить

а) 27; б) 9; в) 4; г) -4

2. Вычислить

3. Вычислить

а) 2; б) 0,5; в) ; г)4

4. Вычислить

а)75; б) 35; в) lg25; г) 3

5. Вычислить

а) 6; б) 2; в) -2; г) -6

6. Вычислить

а) 35; б) 4; в) 2; г) -35

7. Вычислить

8. Вычислить

9. Определить , если

а) 3a+ 2b; б)2a+ 3b;

в) a - b; г) a + b

10. Вычислить

а) 2; б) 0,5; в) 1; г) -1

1. Вычислить

а) 25; б) -3; в) 4; г) 3

2. Вычислить

3. Вычислить

а) 3; б) 0; в) 1; г) 4

4. Вычислить

а)4; б) 64; в) lg64; г) 16; .

5. Вычислить

а) 10; б) 8; в) 2; г) 4

6. Вычислить

а) 6; б) 2; в) -6; г) -2

7. Вычислить

а) 25; б) 2; в) 4; г) -25

a) 2; б) 1; в) 0,5; г)

9. Определить если

а) 3 a+ 2b; б) 1 + a + b;

в) a + b; г) a - b

10. Вычислить

а) -2; б) -1; в) 1 г) 2

1. Вычислить

а) -2; б) 2; в) 4; г) -4

2. Вычислить

3. Вычислить

а) 3; б) 0; в) 1; г) 2

4. Вычислить

а)16; б) 5; в) lg16; г)30; .

5. Вычислить

а) 10; б) 4; в) 8; г) 0,5

6. Вычислить

а) 4; б) 3; в) 5; г) 10;

7. Вычислить

а) 7; б) 2; в) -2; г) -7

8. Вычислить

a) 1; б) 0,5; в) 2; г)

9. Определить , если

а) 2 a+ 3b;б) 2( a + b);

в) 3 a + b;г) a + b

10. Вычислить

а) 2; б) 1; в) -2 г) -1

1. Вычислить

а) 2; б) -2; в) 5; г) -5

2. Вычислить

3. Вычислить

а) 1; б) 0; в) -1; г) 5

4. Вычислить

а) 9; б) lg9; в) 3; г) 24; .

5. Вычислить

а) 3; б) 4; в) 10; г) 0,5

6. Вычислить

а) 3; б) 5; в) 4; г) 17

7. Вычислить

а) 15; б) 4; в) -15; г) 2

8. Вычислить

a) ; б) 2; в) 0,5; г)1

9. Определить,если

а) 2 a+ b; б) 1 + a + b;

в) 3 a + b; г)1 + 2 a + b

10. Вычислить

а) -1; б) 1; в) 2 г) -2

Свойства логарифмов

Вариант – 5

Вариант – 6

Вариант – 7

Вариант – 8

1. Вычислить

а) 4; б) 9; в) 2; г) -2

2. Вычислить

3. Вычислить

а) 2; б) -1; в) ; г)0,5

4. Вычислить

а) 5; б)32; в) lg32; г) 6

5. Вычислить

а) 6; б) 2; в) -2; г) -6

6. Вычислить

а)24; б) 4; в) 2; г) – 24

7. Вычислить

8. Вычислить

9. Определить , если

а) 2a+ 2b;б) 3a+ 2b;

в) a - b; г) a + b

10. Вычислить

а) 2; б) 0,5; в) 1; г) -1

1. Вычислить

а) 125; б) 3; в) -3; г) 4

2. Вычислить

3. Вычислить

а) 1; б) 3; в) 0,5; г) 4

4. Вычислить

а) 4; б) 78; в) 27; г)lg27; .

5. Вычислить

а) 9; б) 0,5; в) -2; г) 2;

6. Вычислить

а) 7; б) 2; в) -7; г) -2

7. Вычислить

а) 15; б) 4; в) -15; г) 2

a) ; б) 2; в) 0,5; г) 1

9. Определить,если известно, что

а) 3 a+ 2b; б) 1 + a +2 b;

в) 1+ a + b; г) a – b

10. Вычислить

а) -2; б) -1; в) 2 г) 1

1. Вычислить

а) 3; б) 32 в) 4; г) 16

2. Вычислить

3. Вычислить

а) 3; б) 0; в) 2; г) 1

4. Вычислить

а)16; б) 2; в) lg16; г) 4.

5. Вычислить

а) 16; б) 4; в) 8; г) 2

6. Вычислить

а) 1; б) 4; в) 2; г) 9;

7. Вычислить

а) 7; б) 2; в) -2; г) -7

8. Вычислить

a) 0,5; б) 2; в) 1; г)

9. Определить , если известно, что

а) 2 a+ 2b;б) 2( a + b);

в) 1 + 2a +b; г) 1+a + 2b

10. Вычислить

а) 2; б) 1; в) -2 г) -1

1. Вычислить

а) 3; б) -3; в) 9; г) -9

2. Вычислить

3. Вычислить

а) -1; б) 3 в) 1; г) 5

4. Вычислить

а) 9; б) ; в) 2; г) 27; .

5. Вычислить

а) 1; б) 4; в) 3; г) 0,5

6. Вычислить

а) 3; б) 4; в) 5; г) 17

7. Вычислить

а) 15; б) 4; в) 8; г) 2

8. Вычислить

a) 1; б) ; в) 0,5; г) 3

9. Определить , если известно, что

а) 2 a+ b; б) 1 + a + b;

в) 3 a + b; г) 2 + a + b

10. Вычислить

а) -1; б) 1; в) 2; г) -2

Свойства логарифмов

Вариант – 9

Вариант – 10

Вариант – 11

Вариант – 12

1. Вычислить

а) 27; б) 9; в) -4; г) 4

2. Вычислить

3. Вычислить

а) 2; б) 1; в) ; г) 4

4. Вычислить

а)16; б) 60; в) lg16; г) 3

5. Вычислить

а) 6; б) 1; в) 2; г)

6. Вычислить

а) 13; б) 4; в) 2; г) -13

7. Вычислить

8. Вычислить

9. Определить , если

а) 3a+ 2b;б) 2a+ 3b;

в) a - b; г) a + b

10. Вычислить

а) 2; б) 0,5; в) 1; г) -1

1. Вычислить

а) 13; б) 0,5; в) 4; г) 2

2. Вычислить

3. Вычислить

а) 3; б) 0; в) 1; г) 4

4. Вычислить

а) 4; б) 8; в) lg8; г) 12

5. Вычислить

а) 10; б) 8; в) 2; г) 4

6. Вычислить

а) 5; б) 2; в) -5; г) -2

7. Вычислить

а) 8; б) 3; в) 4; г) 16

a) 2; б) 1; в) 0,5; г)

9. Определить , если известно, что

а) 3 a+ 2b; б) 1 + a + b;

в) a + b; г) a - b

10. Вычислить

а) -2; б) 1; в) 0,5 г) 2

1. Вычислить

а) -4; б) -8; в) 4; г) 8

2. Вычислить

3. Вычислить

а) 4; б) 1; в) 2; г) -2

4. Вычислить

a) 15; б) 2; в) lg15; г) lg210

5. Вычислить

а) 0,5; б) 4; в) 8; г) 2

6. Вычислить

а) 4; б) 3; в) 5; г) 16

7. Вычислить

а) 10; б) 2; в) -2; г) 5

8. Вычислить

a) 0,5; б) 2; в) 1; г)

9. Определить , если известно, что

а) 1+ a+ 2b; б) 1+ 2a + b;

в) 1+ a + b; г) a + b

10. Вычислить

а) 2; б) 1; в) -2 г) -1

1. Вычислить

а) 2; б) 0,5 в) -2; г) 5

2. Вычислить

3. Вычислить

а) 1; б) -5; в) -1; г) 5

4. Вычислить

а) ; б) 3; в) ; г) -24; .

5. Вычислить

а) 3; б) 4; в) 5; г) 0,5

6. Вычислить

а) 4; б) 3; в) 5; г) 29

7. Вычислить

а) 9; б) 4; в) 2; г) 3

8. Вычислить

a) 1; б) ; в) 0,5; г) 2

9. Определить , если

а) 1 +2a+ b; б) 1 + a + b;

в) 3 a + b; г) 2 + a + b

10. Вычислить

а) -1; б) 1; в) 2 г) -2

Основные типы логарифмических уравнений:

., где – заданные функции.

Методы решения логарифмических уравнений.
1. Метод решения на основании определения логарифма.	Теорема. Уравнения и равносильны
2. Метод потенцирования.	Пусть – фиксированное положительное число и пусть дано уравнение . Замену этого уравнения уравнением называют потенцированием уравнения . Замечание. Потенцирование уравнения может привести к появлению посторонних корней. Пример. Уравнение lg (x²– 4) = lg (4x – 7) приводит к уравнению – следствию (x²– 4) = (4x – 7), имеющему корень 1, посторонний для исходного уравнения.
Теорема. Уравнение равносильно любой из систем:
Теорема. Уравнение равносильно любой из систем:
Теорема. Уравнение , где – заданные функции равносильно любой из систем:
3. Метод введения новой переменной.	Уравнение Обозначив и, решив полученное квадратное уравнение, придём к уравнению типа 1). Отметим, что часто исходное уравнение сводится к одному из указанных типов после некоторых преобразований.

Тема: Решение логарифмических уравнений.		Тема: Решение логарифмических уравнений.
I Карточка		I Карточка
Задание: решите уравнение		Задание: решите уравнение
Решение:		Решение:

Ответ:		Ответ:
Решите самостоятельно:	Ответы:	Решите самостоятельно:	Ответы:
1.	1.	1.	1.
2.	2.	2.	2.
3.	3.	3.	3.
4.	4.	4.	4.

Образцы решения логарифмических уравнений

Тема: Решение логарифмических уравнений.		Тема: Решение логарифмических уравнений.
II Карточка		II Карточка
Задание: решите уравнение		Задание: решите уравнение
Решение:		Решение:

Ответ:		Ответ:
Решите самостоятельно:	Ответы:	Решите самостоятельно:	Ответы:
1.	1.	1.	1.
2.	2.	2.	2.
3.	3.	3.	3.
4.	4.	4.	4.

Тема: Решение логарифмических уравнений.

III Карточка

Задание: решите уравнение

Решение:

Ответ:

Решите самостоятельно:

Ответы:

Решите самостоятельно:

Ответы:

IV Карточка		IV Карточка
Задание: решите уравнение		Задание: решите уравнение
Решение:		Решение:
_х		_х
Ответ:		Ответ:
Решите самостоятельно:	Ответы:	Решите самостоятельно:	Ответы:
1.	1.	1.	1.
2.	2.	2.	2.
3.	3.	3.	3.
4.	4.	4.	4.

Тема: Решение логарифмических уравнений.		Тема: Решение логарифмических уравнений.
V Карточка		V Карточка
Задание: решите уравнение		Задание: решите уравнение
Решение:		Решение:
7 11 х		7 11 х
Ответ:		Ответ:
Решите самостоятельно:	Ответы:	Решите самостоятельно:	Ответы:
1.	1.	1.	1.
2.	2.	2.	2.
3.	3.	3.	3.
4.	4.	4.	4.

VI Карточка		VI Карточка
Задание: решите уравнение		Задание: решите уравнение
Решение:		Решение:
0 4 х		0 4 х
Ответ:		Ответ:
Решите самостоятельно:	Ответы:	Решите самостоятельно:	Ответы:
1.	1.	1.	1.
2.	2.	2.	2.
3.	3.	3.	3.
4.	4.	4.	4.

VII Карточка

Задание: решите уравнение

Решение:

1,5

1,5

Ответ:

Решите самостоятельно:

Ответы:

Решите самостоятельно:

Ответы:

Тема: Решение логарифмических уравнений.

VIII Карточка

Задание: решите уравнение

Решение:

Ответ:

Решите самостоятельно:

Ответы:

Тест по теме «Логарифмические уравнения». Вариант 1

Часть А.

А1. Укажите промежуток, содержащий корень уравнения

1) ;

2) ;

3) ;

4) .

А2. Укажите промежуток, содержащий корень уравнения

1) ;

2) ;

3) ;

4) .

А3. Укажите промежуток, содержащий корень уравнения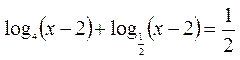

1) ;

2) ;

3) ;

4) .

А4. Найдите произведение корней уравнения

1) 1;

2) 0,5;

3) - 4;

4) - 0,5.

А5. Укажите число корней уравнения

1) 0;

2) 1;

3) 2;

4) 3.

А6. Укажите промежуток, которому принадлежит корень уравнения

1) ;

2) ;

3) ;

4) .

А7. Укажите промежуток, которому принадлежит корень уравнения

1) ;

2) ;

3) ;

4) .

А8. Решите уравнение

1) ;

2) 100; 0,001;

3) - 2; 6;

4) 10.

А9. Найдите корень уравнения

1) 0;

2) 1;

3) 2;

4) 3.4

А10. Найдите сумму корней уравнения

1) 0;

2) 8;

3) 2;

4) 11.

Часть В.

В11. Решите уравнение

В12. Решите уравнение

В13. Решите уравнение

В14. Решите уравнение

В15. Решите уравнение

В16. Решите уравнение

В17. Найдите корень (или произведение корней, если их несколько) уравнения

В18. Найдите корень (или сумму корней, если их несколько) уравнения

В19. Найдите корень (или сумму корней, если их несколько) уравнения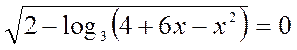

В20. Найдите корень (или произведение действительных, различных корней, если их несколько) уравнения

В21. Найдите корень (или произведение корней, если их несколько) уравнения

В22. Найдите корень (или сумму корней, если их несколько) уравнения

В23. Решите уравнение

Тест по теме «Логарифмические уравнения». Вариант 2.

Часть А.

А1. Укажите промежуток, содержащий корень уравнения

1) ;

2) ;

3) ;

4) .

А2. Укажите число корней уравнения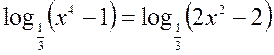

1) 0;

2) 1;

3) 2;

4) 3.

А3. Укажите промежуток, которому принадлежит корень уравнения

1) ;

2) ;

3) ;

4) .

А4. Укажите промежуток, которому принадлежит корень уравнения

1) ;

2) ;

3) ;

4) .

А5. Укажите промежуток, которому принадлежит корень уравнения

1) ;

2) ;

3) ;

4) .

А6. Решите уравнение

1) ;

2) ;

3) ;

4) 3.

А7. Найдите корень уравнения

1) 1;

2) - 1;

3) 2;

4) - 2.

А8. Найдите множество, которому принадлежит корень уравнения

1) ;

2) ;

3) ;

4) .

А9. Найдите сумму квадратов корней уравнения

1) 2;

2) 13;

3) 5;

4) 18.

А10. Найдите отношение большего корня уравнения 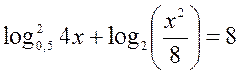к меньшему корню.

1) 4;

2) 128;

3) 8;

4) 256.

Часть В.

В1. Решите уравнение

В2. Решите уравнение

В3. Решите уравнение

В4. Решите уравнение

В5. Решите уравнение

В6. Решите уравнение

В7. Найдите корень (или сумму корней, если их несколько) уравнения

В8. Найдите корень (или сумму корней, если их несколько) уравнения

В9. Найдите корень (или сумму корней, если их несколько) уравнения

В10. Найдите корень (или сумму корней, если их несколько) уравнения

В11. Найдите корень (или сумму корней, если их несколько) уравнения

В12. Найдите корень (или сумму корней, если их несколько) уравнения

В13. Укажите число корней уравнения

Набор заданий для систематизации знаний для решения логарифмических уравнений
Вариант 1	Вариант 2		Вариант 3		Вариант 4
Решите уравнения	Решите уравнения		Решите уравнения		Решите уравнения


*Логарифмические уравнения*	*Логарифмические уравнения*		*Логарифмические уравнения*		*Логарифмические уравнения*
Вариант 5	Вариант 6		Вариант 7		Вариант 8
Решите уравнения	Решите уравнения		Решите уравнения		Решите уравнения

*Логарифмические уравнения*		*Логарифмические уравнения*		*Логарифмические уравнения*		*Логарифмические уравнения*
Вариант 9		Вариант 10		Вариант 11		Вариант 12
Решите уравнения		Решите уравнения		Решите уравнения		Решите уравнения

Лист контроля по теме: «Логарифмическая функция»[1]

Студента (ки)__________________________________ Группы ____________

I. Вычислите		II. Найти О.О.Ф.			III. Решите уравнение			IV. Решите неравенство
Вариант задания	Отметка Выполн		Вариант задания	Отметка Выполн		Вариант задания	Отметка Выполн	Вариант задания	Отметка Выполн	Вариант задания	Отметка Выполн
В. 31-1			В. 5-1			В. 1-2		В. 4-2		В. 54-2
В. 63-1			В. 13-1			В. 12-2		В. 7-2		В. 56-2
В. 72-1			В. 21-1			В. 17-2		В. 8-2		В. 58-2
В. 82-1			В. 29-1			В. 18-2		В. 10-2		В. 60-2
В. 87-1			В. 33-1			В. 26-2		В. 14-2		В. 62-2
В. 91-1			В. 37-1			В. 28-2		В. 16-2		В. 64-2
			В. 41-1			В. 34-2		В. 20-2		В. 66-2
			В. 45-1			В. 36-2		В. 22-2		В. 67-2
			В. 53-1			В. 42-2		В. 24-2		В. 69-2
			В. 55-1			В. 44-2		В. 25-2		В. 70-2
			В. 61-1			В. 51-2		В. 32-2		В. 71-2
			В. 80-1			В. 73-2		В. 38-2		В. 81-2
			В. 88-1			В. 74-2		В. 40-2		В. 83-2
			В. 90-1			В. 76-2		В. 46-2		В. 86-2
			В. 94-1			В. 79-2		В. 48-2		В. 89-2
			В. 95-1			В. 93-2		В. 50-2

Количество вариантов:

· Дифференцированный набор заданий по теме «Понятие логарифма» —(3)

· Дифференцированный набор заданий для систематизации знаний «Свойства логарифма» — (12)

· Карточки :Решение логарифмических уравнений — (4)

· Набор заданий для систематизации знаний для решения логарифмических уравнений — (12)

Заключение

Данное учебно-методическое пособие было апробировано авторами в течении 3-х лет в учебных группах по различным специальностям (СПО) на обучающихся 1 курса средних профессиональных учебных заведений, осуществляющих обучение на базе основного общего образования.

Данное пособие в 2017г. было востребовано на занятиях по математике как в группах СПО на 1-м курсе, так и было использовано на 2-м курсе в группе НПО (при изучении темы: «Логарифмы»).

Пособие предназначено для реализации ФГОС к минимуму содержания и уровню подготовки студентов по дисциплине «Математика». В рабочей программе (п.1.3 Цели и задачи учебной дисциплины – требования к результатам освоения учебной дисциплины) указано, что — студент должен

иметь представление:

о роли математики в современном мире, общности ее понятий и представлений;

о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;

знать:

определение логарифма с произвольным основанием;

основные логарифмические тождества;

способы решения простейших логарифмических уравнений;

уметь:

применять определение логарифма с произвольным основанием;

применять основные логарифмические тождества при выполнении конкретных заданий;

применять способы решения простейших логарифмических уравнений.

Все эти понятия и приемы решения уравнений и были представлены в пособии.

Данное пособие при организации аудиторной и самостоятельной работы дает возможность преподавателю формировать соответствующие ОК. (Приложение1).

Приложение1

Требования к деятельности обучающихся по уровням сформированности общих компетенций

ОК (шифр, согласно стандартам)	Аспект общей компетенции	Уровень I	Уровень II	Уровень III	Уровень IV
*Компетенции в сфере самоорганизации и самоуправления*
ОК 2	ОК 2.1. Планирование деятельности	корректно воспроизводит технологию по инструкции	планирует деятельность по решению задачи в рамках заданных (известных) технологий, в том числе выделяя отдельные составляющие технологии	разбивает поставленную цель на задачи, подбирая из числа известных технологии (элементы технологий), позволяющие решить каждую из задач
	ОК 2.2. Планирование ресурсов	называет ресурсы для решения поставленной задачи в соответствии с заданным способом деятельности	анализирует потребности в ресурсах и планирует ресурсы в соответствии с заданным способом решения задачи
	ОК 2.3. Определение методов решения профессиональных задач			выбирает способ (решения задачи в соответствии с заданными условиями и имеющимися ресурсами
ОК 3	ОК 3.1. Анализ рабочей ситуации	анализирует рабочую ситуацию в соответствии с заданными критериями, указывая ее соответствие \ несоответствие эталонной ситуации	самостоятельно задает критерии для анализа рабочей ситуации на основе заданной эталонной ситуации
	ОК 3.2. Текущий контроль и коррекция деятельности	осуществляет текущий контроль своей деятельности по заданному алгоритму	планирует текущий контроль своей деятельности в соответствии с заданной технологией деятельности и определенным результатом (целью) или продуктом деятельности	предлагает способ коррекции деятельности на основе результатов текущего контроля	предлагает способ коррекции деятельности на основе результатов оценки продукта
	ОК 3.3. Оценка результатов деятельности	оценивает продукт своей деятельности по характеристикам	оценивает продукт своей деятельности на основе заданных критериев	оценивает результаты деятельности по заданным показателям
	ОК 3.4. Принятие ответственного решения			выбирает способ разрешения проблемы в соответствии с заданными критериями и ставит цель деятельности	задает критерии для определения способа разрешения проблемы
				оценивает последствия принятых решений
				проводит анализ ситуации по заданным критериям и называет риски
				анализирует риски (определяет степень вероятности и степень влияния на достижение цели) и обосновывает достижимость цели	предлагает способы предотвращения и способы нейтрализации рисков
ОК 8 (СПО)	ОК 8.1. Оценка собственного продвижения	называет трудности, с которыми столкнулся при решении задачи и предлагает пути их преодоления \ избегания в дальнейшей деятельности	указывает «точки успеха» и «точки роста» указывает причины успехов и неудач в деятельности [2]	анализирует \ формулирует запрос на внутренние ресурсы (знания, умения, навыки, способы деятельности, ценности, установки, свойства психики) для решения профессиональной задачи
*Компетенции в сфере работы с информацией*
ОК 4	ОК 4.1. Поиск информации	выделяет из содержащего избыточную информацию источника информацию, необходимую для решения задачи	самостоятельно находит источник информации по заданному вопросу
	ОК 4.1. Поиск информации		указывает на недостаток информации, необходимой для решения задачи	формулирует вопросы, нацеленные на получение недостающей информации
	ОК 4.2. Извлечение и первичная обработка информации	извлекает информацию по одному основанию из одного или нескольких источников и систематизирует ее в рамках заданной структуры	извлекает информацию по двум и более основаниям из одного или нескольких источников и систематизирует ее в рамках заданной структуры	извлекает информацию по двум и более основаниям из одного или нескольких источников и систематизирует ее в самостоятельно определенной в соответствии с задачей информационного поиска структуре
	ОК 4.3. Обработка информации	выделяет в источнике информации вывод и \ или аргументы, обосновывающие определенный вывод	делает вывод об объектах, процессах, явлениях на основе сравнительного анализа информации о них по заданным критериям или на основе заданных посылок и \ или приводит аргументы в поддержку вывода	делает вывод о применимости общей закономерности в конкретных условиях	делает обобщение на основе предоставленных эмпирических или статистических данных
*Компетенции в сфере коммуникации*
ОК 6	ОК 6.1. Работа в команде (группе)	участвует в групповом обсуждении, высказываясь в соответствии с заданной процедурой и по заданному вопросу	договаривается о процедуре и вопросах для обсуждения в группе в соответствии с поставленной целью деятельности команды (группы)	принимает и фиксирует решение по всем вопросам для группового обсуждения	фиксирует особые мнения; использует приемы выхода из ситуации, когда дискуссия зашла в тупик, или резюмирует причины, по которым группа не смогла добиться результатов обсуждения
	ОК 6.1. Работа в команде (группе)	при групповом обсуждении: аргументированно отвергает или принимает идеи	при групповом обсуждении: задает вопросы, при групповом обсуждении: убеждается, что в группе поняли предложенную идею	при групповом обсуждении: развивает и дополняет идеи других (разрабатывает чужую идею)	дает сравнительную оценку идей, высказанных участниками группы, относительно цели групповой работы
	ОК 6.2. Эффективное общение: монолог	соблюдает нормы публичной речи и регламент, использует паузы для выделения смысловых блоков своей речи, использует вербальные средства (средства логической связи) для выделения смысловых блоков своей речи	соблюдает заданный жанр высказывания (служебный доклад, выступление на совещании \ собрании, презентация товара / услуг)	использует средства наглядности или невербальные средства коммуникации
	ОК 6.3. Эффективное общение: диалог	начинает и заканчивает разговор в соответствии с нормами; отвечает на вопросы, направленные на выяснение фактической информации	отвечает на вопросы, направленные на выяснение мнения (позиции); задает вопросы, направленные на выяснение фактической информации	запрашивает мнение партнера по диалогу
	ОК 6.3. Эффективное общение: диалог	извлекает из устной речи (монолог, диалог, дискуссия) основное (общее) содержание фактической информации	извлекает из устной речи (монолог, диалог, дискуссия) требуемое содержание фактической информации и логические связи, организующие эту информацию	извлекает из устной речи (монолог, диалог, дискуссия) фактическую и оценочную информацию, определяя основную тему, звучавшие предположения, аргументы, доказательства, выводы, оценки
	ОК 6.4. Эффективное общение: письменная коммуникация	создает стандартный продукт письменной коммуникации простой структуры

Скачано с www.znanio.ru

[1]

Севастопольское государственное бюджетное образовательное учреждение профессионального образования «Севастопольский медицинский колледж имени

ЛОГАРИФМЫ » Дисциплина: «МАТЕМАТИКА»

Аннотация: Учебно-методическое пособие по теме «

Оглавление Пояснительная записка

Изобретение логарифмов, сократив работу астронома, продлило ему жизнь»

Использование пособия на различных этапах занятия предполагает экономию времени и усилий (преподавателя, студента) за счет компактного изложения теоретического материала; иллюстрации каждой формулы примерами; подробно разобранных…

Критерии оценок: Отметка «5» ставится, если: · работа выполнена полностью; · в логических рассуждениях и обосновании решения нет пробелов и ошибок; · в решении нет…

Откуда взялся Log? Мы изучили показательные уравнения

Теперь, представим (2) показательное уравнение в виде логарифма и попробуем решить его: = 30 х = 30

Свойства логарифмов ТОЖДЕСТВЕННЫЕ

Задача Вычислите логарифм:

Дифференцированный набор заданий по теме «Понятие логарифма» 1 вариант 2 вариант 3 вариант

Вычислить: Вычислить:

Свойства логарифмов (образцы решения)

Другие виды обозначения логарифмов: логарифм числа b по основанию e ( натуральный логарифм ) e = 2,718281828459045… – основание натурального логарифма; логарифм числа b по…

Сложение и вычитание логарифмов

Вынесение показателя степени из логарифма

Задача Найдите значение выражения:

Переход к новому основанию

Задача Найдите значение выражения:

Основное логарифмическое тождество

Набор заданий для систематизации знаний

Представьте логарифм произведения в виде суммы логарифмов: 21) 22) 23) 24) 25)

Представьте выражение в виде логарифма степени: 46) 2log 2 a 47) log 2 b 48) 2ln 49) 3log 11 50) m lg3

ТЕМА: ЛОГАРИФМЫ Задание: вычислите

Допишите формулы, если это возможно

ТЕМА: ЛОГАРИФМЫ Задание: вычислите 1

Дифференцированный набор заданий для систематизации знаний «Свойства логарифма»

Свойства логарифмов Свойства логарифмов

Основные типы логарифмических уравнений : 1

Методы решения логарифмических уравнений

Тема: Решение логарифмических уравнений

IV Карточка

Тема: Решение логарифмических уравнений

VI Карточка

VII Карточка

Тема: Решение логарифмических уравнений

Тест по теме «Логарифмические уравнения»

Часть В. В11. Решите уравнение

Тест по теме «Логарифмические уравнения»

Часть В. В1. Решите уравнение

Набор заданий для систематизации знаний для решения логарифмических уравнений

Логарифмические уравнения

Лист контроля по теме: «Логарифмическая функция» [1]

Количество вариантов: ·

Заключение Данное учебно-методическое пособие было апробировано авторами в течении 3-х лет в учебных группах по различным специальностям (СПО) на обучающихся 1 курса средних профессиональных учебных…

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

03.05.2024

Методическая разработка практического занятия Тема ”Логарифм числа и его свойства ”

Пояснительная записка

Откуда взялся Log?

Свойства логарифмов

Дифференцированный набор заданий по теме «Понятие логарифма»

Свойства логарифмов (образцы решения)

Набор заданий для систематизации знаний

Дифференцированный набор заданий для систематизации знаний «Свойства логарифма»

Образцы решения логарифмических уравнений

Набор заданий для систематизации знаний для решения логарифмических уравнений

Лист контроля по теме: «Логарифмическая функция»[1]

Количество вариантов:

Заключение

Приложение1

Севастопольское государственное бюджетное образовательное учреждение профессионального образования «Севастопольский медицинский колледж имени

ЛОГАРИФМЫ » Дисциплина: «МАТЕМАТИКА»

Аннотация: Учебно-методическое пособие по теме «

Оглавление Пояснительная записка

Изобретение логарифмов, сократив работу астронома, продлило ему жизнь»

Критерии оценок: Отметка «5» ставится, если: · работа выполнена полностью; · в логических рассуждениях и обосновании решения нет пробелов и ошибок; · в решении нет…

Откуда взялся Log? Мы изучили показательные уравнения

Теперь, представим (2) показательное уравнение в виде логарифма и попробуем решить его: = 30 х = 30

Свойства логарифмов ТОЖДЕСТВЕННЫЕ

Задача Вычислите логарифм:

Дифференцированный набор заданий по теме «Понятие логарифма» 1 вариант 2 вариант 3 вариант

Вычислить: Вычислить:

Вычислить: Вычислить:

Свойства логарифмов (образцы решения)

Другие виды обозначения логарифмов: логарифм числа b по основанию e ( натуральный логарифм ) e = 2,718281828459045… – основание натурального логарифма; логарифм числа b по…

Сложение и вычитание логарифмов

Вынесение показателя степени из логарифма

Задача Найдите значение выражения:

Переход к новому основанию

Задача Найдите значение выражения:

Основное логарифмическое тождество

Набор заданий для систематизации знаний

Представьте логарифм произведения в виде суммы логарифмов: 21) 22) 23) 24) 25)

Представьте выражение в виде логарифма степени: 46) 2log 2 a 47) log 2 b 48) 2ln 49) 3log 11 50) m lg3

ТЕМА: ЛОГАРИФМЫ Задание: вычислите

Допишите формулы, если это возможно

ТЕМА: ЛОГАРИФМЫ Задание: вычислите 1

Дифференцированный набор заданий для систематизации знаний «Свойства логарифма»

Свойства логарифмов Свойства логарифмов

Свойства логарифмов Свойства логарифмов

Основные типы логарифмических уравнений : 1

Методы решения логарифмических уравнений

Тема: Решение логарифмических уравнений

Тема: Решение логарифмических уравнений

Тема: Решение логарифмических уравнений

IV Карточка

Тема: Решение логарифмических уравнений

VI Карточка

VII Карточка

Тема: Решение логарифмических уравнений

Тест по теме «Логарифмические уравнения»

Часть В. В11. Решите уравнение

Тест по теме «Логарифмические уравнения»

Часть В. В1. Решите уравнение

Набор заданий для систематизации знаний для решения логарифмических уравнений

Логарифмические уравнения

Лист контроля по теме: «Логарифмическая функция» [1]

Количество вариантов: ·