
 Муниципальное
общеобразовательное учреждение
Муниципальное
общеобразовательное учреждение
Брейтовская средняя общеобразовательная школа
Методическая разработка на тему:
«Проблемно-диалогическое обучение как средство повышения эффективности деятельности школьников на уроках математики в условиях
реализации ФГОС ООО»
Автор:
Бисева Ольга Сергеевна,
учитель математики (высшая квалификационная категория)
Брейтово, 2019 г.
Содержание
|
ВВЕДЕНИЕ |
3-4 |
|
ГЛАВА I. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПРОБЛЕМНО- ДИАЛОГИЧЕСКОГО ОБУЧЕНИЯ
|
5 |
|
1.1. Сравнительный анализ изложения в различных источниках |
5 |
|
1.2. Сравнение традиционного и проблемного обучения |
5-6 |
|
1.3. Сущность и структура понятия «проблемно-диалогическая технология» |
6-8 |
|
1.4. Диагностика результативности работы учителя по повышению эффективности деятельности учащихся на уроках математики |
9 |
|
ГЛАВА II. ТЕХНОЛОГИЯ ПРОБЛЕМНО- ДИАЛОГИЧЕС- КОГО ОБУЧЕНИЯ КАК СРЕДСТВА ПОВЫШЕНИЯ ЭФФЕКТИВНОСТИ ДЕЯТЕЛЬНОСТИ ШКОЛЬНИ- КОВ НА УРОКАХ МАТЕМАТИКИ |
10 |
|
2.1. Применение проблемно-диалогической технологии на уроках математики |
10-12 |
|
2.2. Анализ результатов деятельности по повышению эффективности деятельности школьников при применении технологии |
13 |
|
ЗАКЛЮЧЕНИЕ |
14-15 |
|
СПИСОК ЛИТЕРАТУРЫ
|
16 |
|
ПРИЛОЖЕНИЯ |
17 |
|
1. Диагностика результатов применения технологии проблемно –диалогического обучения |
17-19 |
|
2. Дидактические материалы к урокам математики в основной школе (примеры приемов создания проблемных ситуаций)
|
20-27 |
|
3. Конспект урока математики по теме «Деление с остатком» (5 класс) |
28-43 |
|
4. Конспект урока по геометрии по теме «Некоторые свойства прямоугольных треугольников» (7 класс) |
44-54 |
|
5. Технологическая карта урока геометрии по теме: «Площадь треугольника» (8 класс) |
55-64 |
ВВЕДЕНИЕ.
«Проблема сама прокладывает путь к новым знаниям
и способам действия»
М.Марков
Таким образом, важной задачей современной школы является создание необходимых и полноценных условий для личностного и познавательного развития каждого обучающегося, формирование активной позиции, субъективности обучающихся в учебном процессе.
Эффективное решение данной задачи, опираясь на Федеральный Государственный стандарт общего образования, невозможно без осмысленной реализации педагогами в образовательном процессе школы современных педагогических технологий.Одной из них является технология проблемно – диалогического обучения, которая помогает учащимся самостоятельно открывать знания. На смену монологу приходит диалог.При переходе к стандартам нового поколения меняется роль учителя и ученика, меняется стиль их взаимодействия. Ученик – активный, творческий, мыслящий, ищущий участник процесса обучения, который умеет работать с информацией, умеет делать выводы, анализировать, контролировать и оценивать свою деятельность. Учитель же выполняет роль успешного организатора процесса, в котором ученик может развивать все пере-численные выше мыслительные операции.
Большинство ученых признают, что развитие творческих способностей школьников и интеллектуальных умений невозможно без проблемного обучения. Применение данной технологии связано с необходимостью формирования познавательной самостоятельности учащихся, развития их логического, рационального, критического и творческого мышле-ния, и познавательных способностей.
Считаю, что проблемно - диалогическое обучение – одна из наиболее эффективных
технологий, отвечающих современным требованиям ФГОС, так как она позволяет комп-
лексно решать задачи по повышению у учащихся мотивации к изучению предмета, осоз-
нанному пониманию связи математики с жизнью, развитию диалогового общения. А это и
есть залог успешного достижения результата в освоении школьниками математики.
Организация проблемно-диалогического обучения имеет важное
значение для развития мышления школьников, ибо «начало мышления» – в проблемной
ситуации.
Проблемно-диалогическое обучение предполагает организацию поисковой
деятельности обучающихся, овладение знаниями на основе активной умственной
деятельности по решению задач проблемного характера, также овладение методами
добывания знаний.
Данная технология особенно хорошо применима в классах с разным уровнем матема-
тических способностей учащихся, она помогает мне выстраивать свою работу так, чтобы
каждый ученик имел возможность стать активным, творческим, мыслящим участником
процесса обучения, научился самостоятельно добывать конкретную информацию, осмыс-
ливать, интерпретировать и комментировать ее, делать выводы, анализировать, контроли-
ровать и оценивать свою деятельность. При этом я не принуждаю, а побуждаю учащихся к
общению, самостоятельному приобретению знаний, систематизации и применению их на
практике.
Цель моей работы: показать эффективность использования проблемно-диалогического обучения на уроках математики в условиях реализации ФГОС ООО, представить модель педагогической деятельности по «открытию знаний», используя технологию проблемного диалога.
Исходя из этого, основные задачи предполагают:
· обобщить теоретический материал по данной теме;
· провести сравнительный анализ проблемно-диалогического и традиционного способов обучения
· осуществить обучение математики в 5-8 классах с применением приёмов проблемно-диалогического обучения
· создать банк материалов к урокам с использованием проблемного диалога на уроках математики в 5-8 классах.
· найти и апробировать методики определения эффективности использования данной технологии
· обосновать эффективность обучения на уроках математики
Актуальность данной технологии определяется развитием высокого уровня
мотивации к учебной деятельности, активизации познавательных интересов учащихся, что становится возможным при разрешении возникающих противоречий, создании проблемных ситуаций на уроке. В преодолении посильных трудностей у учащихся возникает постоянная потребность в овладении новыми знаниями, новыми способами действий, умениями и навыками.
Проблемно-диалогическое обучение, в отличие от любого другого, способствует не только приобретению учащимися необходимой системы знаний, умений и навыков, но и достижению высокого уровня их умственного развития, формированию у них способности к самообучению, самообразованию.
Данный вид обучения ориентируется на личность учащегося, получающего в условиях такого обучения возможность мыслить и действовать творчески.
Обучающийся в процессе обучения сам конструирует, решает проблемы, строит логические выводы, развивает навыки вдумчивой работы с информацией. Практическая значимость состоит в том, что разработанные конспекты уроков с использованием технологии проблемного диалога могут использоваться учителями математики основной школы.
Новизна опыта состоит в совершенствовании средств обучения и развития учащихся, использовании педагогических инноваций в процессе формирования коммуникативной компетенции учащихся, в создании системы применения методов и приёмов, нацеленных на развитие познавательной и творческой активности учащихся.
Применение технологии проблемно-диалогическогообучения позволяет мне разви-вать у учащихся познавательный интерес к предмету, формировать УУД, делать учебный материал для школьников понятным и интересным, показывать значимость предмета в
жизни людей, а значит, решать главную задачу – повышать уровень математического
образования. Эта технология универсальна: ведь открывать знания можно на любом предмете, в любом классе. Она построена на принципах развивающего обучения и поз-воляет заменить урок объяснения нового материала уроком «открытия» знаний.
Технология проблемно-диалогического обучения – это ключ к успеху и творчеству
как для ученика, так и для учителя.
ГЛАВА I. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПРОБЛЕМНО-
ДИАЛОГИЧЕСКОГО ОБУЧЕНИЯ
1.1.Сравнительный анализ изложения в различных источниках
Теория проблемно-диалогического обучения разрабатывалась в отечественной и мировой педагогике с середины 50-х годов XX столетия. Сегодня теория проблемного обучения – достаточно глубоко разработанная отрасль педагогической науки. Чем вызва-но ее возникновение?
Можно указать несколько причин. До середины 50-х годов методы обучения исследо-вались с точки зрения деятельности учителя. Но позже пришли к выводу, что обучение – бинарный, двусторонний процесс, что при изучении этого процесса важно исследовать и деятельность учителя, и деятельность учащихся. Появилось несколько концепций деятель-ности обучаемых в учебном процессе. Одной из таких концепций является и теория проб-лемного обучения. Возникновение теории проблемного обучения вызвано потребностями самого учебного процесса. Вторая причина возникновения теории проблемного обучения-общественная, социальная потребность в активной, самостоятельной, творческой, само-развивающейся личности способной жить и трудиться в условиях научно- технической революции. Ещё в 60 годы неоспоримо доказали, что ученик на уроке должен ставить и решать проблемы непременно в диалоге с учителем. В трудах А.А.Леонтьева, С.Л. Рубин-штейна, А.М. Матюшкина одновременно утверждается принцип проблемности и диало-гичности учебной деятельности.
На основе многолетних отечественных
исследований в двух самостоятельных областях - проблемном обучении (И.А.
Ильницкая, В.Т. Кудрявцев, М.И.Махмутов и др.) и психологии творчества (А.В.
Брушлинский, A.M.Матюшкин, А.Т. Шумилин и др.) - разработана технология
проблемно-диалогического обучения, которая позволяет заменить урок объяснения
нового материала уроком «открытия» знаний.![]()
Проблемно-диалогическое обучение - это тип обучения, обеспечивающий творческое усвоение знаний учащимися посредством специально организованного учителем диалога. Это тип обучения, обеспечивающий репродуктивное усвоение .
Что представляет собой проблемное обучение?
Существует несколько взглядов на понятие проблемного обучения.
Так польский ученый-педагог ВицентыОконь понимает проблемное обучение как «совокупность таких действий, как организация проблемных ситуаций, формулирование проблем, оказание ученикам необходимой помощи в решении проблем, проверка этих решений и, наконец, руководство процессом систематизации и закрепления приобретенных знаний.[12]
И. Я. Лернер видит сущность проблемного обучения в том, что «учащийся под руководством учителя принимает участие в решении новых для него познавательных и практических проблем в определенно системе, соответствующей образовательно - воспитательным целям школы» .[7]
Т. В. Кудрявцев суть процесса проблемного обучения видит в выдвижении перед учащимися дидактических проблем, в их решении и овладении учащимися обобщенными знаниями и принципами проблемных задач.
Анализ литературы позволяет определить проблемно – диалогическое обучение как тип обучения, обеспечивающий творческое усвоение знаний учащимися посредством диалога с учителем.
1.2 Сравнение традиционного и проблемно-диалогического обучения
Чем проблемное отличается от традиционного?
В традиционном обучении (объяснительно-иллюстративном) учитель сообщает учащемуся готовые знания - он объясняет новый материал, показывает выдвигаемые положения, подкрепляет их иллюстрациями и т. д. Учащийся воспринимает сообщаемое, осмысливает его, запоминает, заучивает.
При проблемном обучении учитель не сообщает знаний в готовом виде, а ставит перед учеником задачу, заинтересовывает его, пробуждает у него желание найти средства для ее разрешения. В поисках этих средств и путей учащийся и приобретает новые знания. В первом типе обучения упор делается на мотивы непосредственного побуждения; (учитель интересно рассказывает, привлекает наглядные пособия - ученику интересно, он активно слушает) или перспективно побуждающие (урок не очень интересен, иллюстративного материала нет, но данный предмет или раздел очень важен для подготовки к экзаменам в вуз, поэтому учителя надо слушать и материал знать). При проблемном обучении ведущими являются мотивы интеллектуального побуждения - учащиеся сами с интересом ищут пути получения недостающих знаний, испытывая удовлетворение от процесса интеллектуального труда, преодоления сложностей и самостоятельно найденного решения [7].
1.3 Основные понятия проблемно-диалогического обучения
В сложном прилагательном «проблемно- диалогическое» первая часть означает, что на уроке изучения нового материала должны быть проработаны два звена: постановка учебной проблемы и поиск решения. Постановка учебной проблемы – это этап формулирования темы урока или вопроса для исследования. Поиск решения – это этап формулирования нового знания. Слово «диалогическое» означает, что постановку учебной проблемы и поиск ее решения осуществляют ученики в ходе специально организованного учителем диалога. Мы различаем два вида диалога: побуждающий и подводящий. Они имеют разную структуру, обеспечивают разную учебную деятельность и развивают разные стороны психики учащихся.
Побуждающий диалог состоит из отдельных стимулирующих реплик, которые помогают ученику работать по-настоящему творчески. На этапе постановки проблемы этот диалог применяется для того, чтобы ученики осознали противоречие, заложенное в проблемной ситуации, и сформулировали проблему. На этапе поиска решения учитель побуждает учеников выдвинуть и проверить гипотезы, т.е. обеспечивает «открытие» знаний путем проб и ошибок. Данный диалогпоэтому развивает творческие способности учащихся.
Подводящий диалог представляет собой систему вопросов и заданий, которая активизирует и, соответственно, развивает логическое мышление учеников. На этапе постановки проблемы учитель пошагово подводит учеников к формулированию темы. На этапе поиска решения он выстраивает логическую цепочку умозаключений, ведущих к новому знанию. Подводящий диалог соответственно развивает логическое мышление учеников.
По определению Е.Л. Мельниковой
1.Побуждающий диалог — это «экскаватор», который выкапывает проблему, вопрос, трудность, т.е. помогает формулировать учебную задачу.
2.Подводящий диалог — это логически выстроенная цепочка заданий и вопросов — «локомотив», движущийся к новому знанию, способу действия.
Постановка учебной проблемы.
|
Подводящий к теме диалог.
|
Побуждающий от проблемнойситуации диалог |
|
вопросы и задания могут различаться по характеру и степени трудности, но должны быть посильными для учеников. Последний вопрос содержит обобщение и позволяет ученикам сформулировать тему урока. По ходу диалога необходимо обеспечивать безоценочное принятие ошибочных ответов учащихся. |
представляет собой сочетание приема создания проблемной ситуации и специальных вопросов, стимулирующих учеников к осознанию противоречия и формулированию учебной проблемы. |
|
+ Развивает логическое
мышление путем |
+ развитие творческого мышления - может затянутся по времени.
|
Суть проблемного обучения состоит в организации педагогом для учащихся проблемных ситуаций, осознании этих ситуаций, их принятия и решения в процессе совместной взаимодействия учащихся и учителя при максимальной самостоятельности учеников и общем направляющем руководстве педагога. (табл.1)
Таблица1. Деятельность учителя и ученика в условиях проблемного обучения
|
Деятельность учителя |
Деятельность ученика |
|
-создает проблемную ситуацию -организует размышление над проблемой и ее формулировкой -организует поиск гипотезы -организует проверку гипотезы -организует обобщение результатов и применение полученных знаний |
-осознают противоречия -формирует проблему -выдвигают гипотезы, объясняющие явления -проверяют гипотезу в эксперименте, решении задач -анализируют результаты, делают выводы -применяют полученные знания |
Проблемная ситуация в обучении – это спланированное, специально задуманное средство, направленное на пробуждение интереса у обучающихся к обсуждаемой теме.
Проблемная ситуация - это интеллектуальное затруднение человека, возникающее в случае, когда он не знает, как объяснить возникшее явление, факт, процесс действительности, не может достичь цели известным ему способом, действие это побуждает человека искать новый способ объяснения или способ действия. Проблемная ситуация есть закономерность продуктивной, творческой познавательной деятельности. Она обуславливает начало мышления в процессе постановки и решения проблем [12.С.14].
Десять способов создания проблемной ситуации по М.И. Махмутову:
• Побуждение учащихся к теоретическому объяснению явлений, фактов, внешнего несоответствия между ними.
• Использование учебных и жизненных ситуаций, возникающих при выполнении учащимися практических заданий в школе, дома или на производстве, в ходе наблюдений за природой.
• Постановка учебных практических заданий на объяснение явления или поиск путей его практического применения.
• Побуждение учащихся к анализу фактов и явлений действительности, порождающему противоречия между житейскими представлениями и научными понятиями об этих фактах.
• Выдвижение предположений (гипотез), формулировка выводов и их опытная проверка.
• Побуждение учащихся к сравнению, сопоставлению и противопоставлению фактов, явлений, правил, действий, в результате которых возникает проблемная ситуация.
• Побуждение учащихся к предварительному обобщению новых фактов.
• Ознакомление учащихся с фактами, носящими как будто бы необъяснимый характер и приведшими в истории науки к постановке учебной проблемы.
• Организация межпредметных связей.
• Варьирование задачи, переформулировка вопроса.
Мыслительная деятельность учащихся стимулируется постановкой вопросов. Вопрос учителя должен быть сложным настолько, чтобы вызвать затруднение учащихся, и в то же время посильным для самостоятельного нахождения ответа.
Учитель на своём уроке, создавая проблемные ситуации и организуя деятельность учащихся по решению учебных проблем, обеспечивает оптимальное сочетание их самостоятельной поисковой деятельности с усвоением готовых выводов науки.
Смысл технологии проблемного диалога заключается в том, чтобы на уроке изучения нового материала «пропустить» школьников через все звенья научного творчества. Проделать такую работу на уроке дети могут только в диалоге с учителем. Поскольку проблема и решение педагогу известны заранее, то он может выбрать вид диалога: побуждающий или подводящий.
Постановка учебной задачи происходит в форме побуждающего диалога, а её решение – в форме подводящего диалога. Подводящий диалог представляет собой систему вопросов и заданий, которые пошагово подводят учащихся к формулированию темы. На этапе поиска решения учитель выстраивает логическую цепочку к новому знанию, ведёт к «открытию».
В структуре урока при проблемном обучении принято выделять четыре основных этапа:
1) осознание проблемной ситуации;
2) анализ ситуации и формулировка проблемы;
3) решение проблемы: выдвижение гипотез и обоснование путей решения, отбор наиболее логичных гипотез и их последовательная проверка;
4) проверка правильности решения.
Основным звеном проблемного обучения является проблемная ситуация.
Проблемные ситуации возникают, например, в таких случаях:
- если обнаруживается несоответствие между уже известными учащимся фактами и новыми знаниями;
- если учащиеся сталкиваются с новыми для них условиями использования уже имеющихся знаний, умений и навыков;
- если необходимо выбрать из известных ученику способов решения учебно-познавательной задачи единственный правильный или наилучший и т.д.
Такая структура урока развивает навыки самостоятельной работы, обеспечивает повы-шение познавательной активности и мотивации учащихся, формирует умения применять ранее усвоенные знания в новой ситуации, творчески их преобразовывать, способствует развитию интеллектуальных способностей школьников. Создание проблемных ситуаций, их анализ, активное участие учеников в поиске путей решения поставленной учебной проблемы возбуждает мыслительную активность учащихся, поддерживает глубокий познавательный интерес.
При введении знаний ученик может пройти два творческих звена: постановку учебной проблемы и поиск решения. Каждое можно организовать тремя методами.
Методы обучения при использовании технологии проблемного диалога
|
Методы |
Проблемно-диалогические |
||
|
постановки проблемы |
побуждающий от проблемной ситуации диалог |
подводящий к теме диалог |
сообщение темы с мотивирующим приемом |
|
поиска решения |
побуждающий к выдвижению и проверке гипотез диалог |
подводящий от проблемы диалог |
подводящий без проблемы диалог |
1.4Диагностика результативности работы учителя по повышению эффективности деятельности учащихся на уроках математики
Неотъемлемым компонентом образовательного процесса является диагностика, с помощью которой определяется результат достижения поставленных учителем целей. В понятие «диагностика» вкладывается более широкий и глубокий смысл, чем в понятие «проверка знаний, умений и навыков» учащихся. Последнее только констатирует результаты, не объясняя их происхождения. В то время как диагностирование включает контроль, проверку, оценивание, накопление статистических данных, их анализ, рассматривает результаты с учётом способов их достижения, выявляет тенденции, динамику процесса.
Наука предполагает большой арсенал методов диагностики, среди которых можно выделить наблюдение, анкетирование, беседы, анализ документов и творческих работ учащихся.
О повышении эффективности деятельности школьников на уроках математики будут свидетельствовать результаты педагогической диагностики по следующим критериям:
1) рейтинг предпочтения у учащихся предмета (математика) по следующим категориям (любимый, не любимый, нейтральное отношение). Использовать можно методику «Изучение отношения к учению и к учебным предметам», разработанную Г.Н. Казанцевой. Методика предназначена для качественного анализа предпочтения тех или иных предметов и мотивов учения. Используя результаты этой методики, можно сделать вывод о причинах предпочтения предмета математика у учащихся.
Выборку сделаем по следующим показателям:
- люблю предмет, потому что – данный предмет интересен; нравится, как преподаёт учитель; учитель интересно объясняет; получаю удовольствие при его изучении;
- не люблю предмет, потому что данный предмет не интересен; не нравится, как преподаёт учитель; учитель неинтересно объясняет; не получаю удовольствие при его изучении.
2) Анкетирование:
- самостоятельность на уроке математики;
- активность учащихся при изучении нового материала (анкетирование);
- уверенность в своих силах, т.е создание учителем «ситуации успеха» для каждого
ученика;
- самооценка учащихся по усвоению учебного материала по математике.
Опираясь на результаты диагностических методик мы подтвердим или опровергнем влияние технологии проблемно-диалогического обучения на повышение эффективности деятельности учащихся.
Эти диагностические методы целесообразно использовать в конце учебного года.
ГЛАВА II. ТЕХНОЛОГИЯ ПРОБЛЕМНО- ДИАЛОГИЧЕСКОГО ОБУЧЕНИЯ КАК СРЕДСТВА ПОВЫШЕНИЯ ЭФФЕКТИВНОСТИ ДЕЯТЕЛЬНОСТИ ШКОЛЬНИКОВ НА УРОКАХ МАТЕМАТИКИ
2.1. Применение проблемно-диалогической технологии на уроках математики
Реализация ФГОС потребовала необходимость изменения в методах и формах организации процесса обучения, применение современных образовательных технологий. Основу системно - деятельностного подхода составляет проблемное обучение, поэтому я решила использовать проблемно-диалогическую технологию на уроках математики, доказать её эффективность. Эту технологию я применяю с 2014 года.
Основные задачи внедрения технологии проблемно-диалогического обучения на уроках заключаются в следующем:
Ø учить детей аргументировать, находить и выделять главное, рассуждать, доказывать, находить рациональные пути выполнения задания
Ø развивать у учащихся такие мыслительные операции, как анализ, сравнение и сопоставление фактов и явлений;
Ø формировать навыки поисковой и исследовательской деятельности;
Ø повышать уровень самостоятельности и активности учащихся
Ø формировать чувства уверенности в своих силах, удовлетворение от умственной деятельности;
Ø создавать ситуацию успеха в процессе деятельности учащихся;
Ø развивать коммуникативные умения; воспитывать у учащихся чувство коллективизма и взаимопомощи;
Ø развивать межпредметные связи.
Условия, обеспечивающие наибольшую эффективность:
Четкое следование методике в организации проблемных диалогов, системность в работе приводит к тому, что дети привыкают идти к знаниям самостоятельно, им становится скучно, если это начинает делать учитель.
Проблемные методы отличаются эффективностью, т.к. постановка проблемы обеспечивает познавательную мотивацию учеников, а поиск решения – понимание материала большинством учащихся класса.
Организация проблемного диалога посредством мультимедийных презентаций включает в поиск новых знаний практически каждого ребенка. Современные возможности урока (мультимедийный проектор) позволяют сделать уроки более интересными и запоминающимися. Я объединила организацию проблемных диалогов с демонстрацией мультимедийных презентаций, но использую мультимедийные презентации не только как иллюстративный материал для активизации внимания учащихся современными средствами, но и как возможность прийти к открытиям на уроках более легко и свободно. Благодаря зрительному восприятию, детям легче удерживать логическую цепочку знаний, которые необходимы для осознания создавшегося противоречия, для обозначения проблемы, для открытия новых знаний. Каждый появляющийся новый слайд мультимедийной презентации, предлагаемой мною, либо служит для активизации внимания и мышления учащихся, либо побуждает к выполнению заданий, или идет как подтверждение правильных ответов и выводов, проверки самостоятельной работы по эталону. Демонстрация мультимедийных презентаций на этапах: актуализация знаний, открытие новых знаний, первичное закрепление - оживляет работу учащихся, позволяет в процесс открытия новых знаний включить практически каждого ребенка. Организация проблемных диалогов с использованием мультимедийных презентаций предоставляет учащимся большую возможность «самостоятельно» прийти к открытию новых знаний на уроках. (Приложения 3, 4, 5)
В своей работе использую три способа постановки учебной проблемы:
1. Побуждающий от проблемной ситуации диалог.
2. Подводящий к теме диалог.
3. Сообщение темы с мотивирующим приемом.
1. Побуждающий от проблемной ситуации диалог.
7 класс. Алгебра. Тема «Свойства степени с натуральным показателем»
|
Учитель |
Ученик |
|
-Ребята! Посмотрите на выражения, записанные на слайде. |
Видят выражения: а3+а2; а3-а2; а3∙а2; а3:а2; (а3)2 |
|
- Как вы думаете, какие действия можно выполнить со степенями? |
Высказывают различные мнения. (Возникла проблемная ситуация) |
|
- Вопрос был задан один, а сколько мы услышали мнений? |
- Мнений было высказано много различных. (Возникло противоречие) |
|
- Ребята! Так чего же мы с вами пока не знаем, какой перед нами возникает вопрос? - Записываем вопрос на доске. |
Формулируют вопрос. - Какие же действия можно выполнять со степенями? |
2
Подводящий
к теме диалог.
Урок
математики 6 класс «Разложение на простые множители».
|
Учитель |
Ученик |
|
Посмотрите на примеры, записанные на доске. |
На доске записано: 60=2∙2∙3∙5; 25=5∙5; 50=2∙5∙5; 210=30∙7; 45=3∙3∙5; 88=8∙11 |
|
-Что заметили общего? |
- Числа разложили на множители. |
|
- В чём различие? |
- У некоторых чисел все множители – простые числа, а у некоторых нет, но эти множители тоже можно разложить на простые множители. |
|
- Какая же тема нашего урока? |
- Разложение чисел на простые множители. |
3. Сообщение темы
с мотивирующим приёмом.
Приёмы:1) «яркое
пятно» - классу сообщается интригующий материал, связанный с темой,
который захватывает внимание учеников (пример: тема урока зашифрована кросс-ворде,
разгадав который учащиеся открывают тему урока);
2) «актуальность» - состоит в обнаружении смысла,
значимости темы для самих учеников.
Урок математики 5 класс «Проценты».
|
Учитель |
Ученик |
|
- Ребята! Тема нашего урока по своему названию вам хорошо знакома. Покупая молоко на упаковке написано 3,2 … Чего? В магазинах на некоторый товар скидка 30….. Чего? Банк даёт населению кредит под несколько…. Чего? - Отвечая на все вопросы, вы дали один и тот же ответ. Так вот тема нашего урока «Проценты». |
Процента. Процентов. Процентов. |
Методы осуществления поиска решения учебной проблемы.
Побуждающий к выдвижению и проверке гипотез диалог представляет собой сочетание специальных вопросов, стимулирующих учеников выдвигать и проверять гипотезы. Данный метод имеет определённую структуру: начинается с общего побуждения (призыва к мыслительной работе), при необходимости подтверждается подсказкой(намёком, сужающим область поиска), в крайнем случае завершается сообщением учителя. При этом общее побуждение представляет собой стандартную готовую реплику, а подсказку необходимо придумывать каждый раз заново.
При выдвижении гипотез побуждающий диалог выглядит так. Общее побуждение осуществляется стандартной репликой «Какие есть гипотезы?», которая провоцирует выдвижение любых гипотез, как ошибочной, так и решающей. Если ученики молчат и выдвигают только ошибочные гипотезы, даётся подсказка к решающей гипотезе, которая продумывается учителем заранее для каждого конкретного урока. Если подсказка не срабатывает, диалог завершается сообщением решающей гипотезы.
При проверке гипотез побуждающий диалог выглядит так. Для устной проверки общее побуждение осуществляется стандартной репликой: «Вы согласны с этой гипотезой? Почему?», подсказка даётся к аргументу или контраргументу, в крайнем случае последние сообщаются в готовом виде. Для практической проверки общее побуждение осуществляется стандартной репликой: «Как нам проверить эту гипотезу?», подсказка даётся к плану проверки, в крайнем случае план сообщается в готовом виде. По хлду диалога учителю необходимо обеспечивать безоценочное принятие любых мыслительных результатов учащихся; ошибочных и решающих гипотез, ошибочных и верных проверок. Поиск решения проблемы может происходить в виде мозгового штурма учащиеся решают проблему по следующему алгоритму:
1. Прочтите внимательно задание и предложите все возможные гипотезы в качестве решений.
2. Сделайте анализ предложенных гипотез и выберите те из них, которые наиболее вероятны и имеют под собой хотя бы частичное научное обоснование.
Подводящий к заданию диалог представляет собой систему(логическую цепочку) посильных ученику вопросов и заданий, которые пошагово приводят класс к формированию нового знания. Решить учебную проблему можно с помощью эвристической беседы.
В работе хочу поделиться различнымиприемами создания проблемной ситуации в учебной деятельности на уроках математики. Каждый из этих способов имеет свою особенность. (Приложение 2).
Проблемный характер изложения учебного материала, организация поисковой, познавательной деятельности учащихся, даёт им возможность переживать радость самостоятельных открытий. При таком ведении урока повышается активность учащихся, их заинтересованность в результатах урока.
При составлении подводящего к теме диалога я подбираю логическую цепочку посильных ученикам вопросов и заданий, которые пошагово приводят класс к формули-
рованию темы урока. В структуру подводящего диалога могут входить разные типы
вопросов и заданий: репродуктивные (вспомнить, выполнить по образцу); мыслительные
(на анализ, сравнение, обобщение). Следует заметить, что все вопросы и задания опирают-ся на уже пройденный классом материал, а последний обобщающий вопрос позволяет ученикам сформулировать тему урока.
Каждому учителю хочется, чтобы на уроке царила атмосфера творчества, чтобы ученики могли сравнивать и ассоциировать, задумываться над проблемными ситуациями и предлагать выход из них. Для этого, безусловно, необходимо творчески мыслить. Можем ли мы научить творческому мышлению? Однозначно ответить нельзя, так как творческие возможности ребёнка закладываются в раннем детстве. А тех, кто не был отягощён интеллектуальным и творческим развитием в дошкольном возрасте, мы можем научить мыслить через поиск. Поэтому технология проблемно-диалогического обучения во многом была принята мной и стала частью проблемного обучения на уроках.
2.2. Анализ результатов психолого-педагогических диагностик по определению эффективности деятельности школьников, обучающихся математике по технологии проблемно-диалогического обучения
Для оценки достижения цели и задач поставленных учителем на уроках математики были использованы следующие методики:
1) Методика«Изучение отношения к учению и к учебным предметам», разработанную
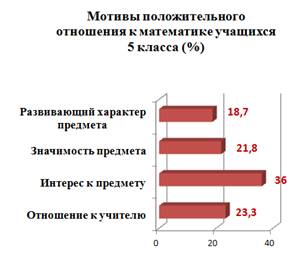
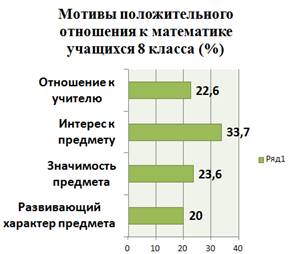
Г.Н. Казанцевой (цель: качественного анализ предпочтения тех или иных предметов и мотивов учения).Анализируя полученные результаты(приложение 1.1), можно отметить, что к числу наиболее значимых мотивов положительного отношения к предмету, отмеченных учащимися 7 класса, относятся: интерес к предмету - 33,7 %, значимость предмета 23,6 %, отношение к учителю -22,6 %, а также развивающий характер предмета – 20%. Учащиеся 5 класса отметили, что наибольшую значимость для них имеют следующие мотивы: интерес к предмету-36%, значимость предмета- 21,8%, развивающий характер предмета- 18,7%, отношение к учителю-23,3%. На основе полученных результатов, можно утверждать, что интерес к предмету сохраняется и является самым значимым мотивом для учащихся.
2) Анкетирование. Цель: выяснить активность, самостоятельность, самооценку учащихся на уроках математики(приложение1.2). Согласно полученным результатам, можно сделать следующие выводы:
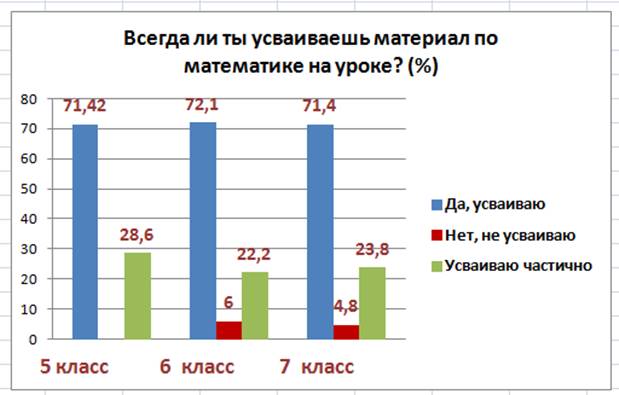
- Был определён процент обучающихся 5-7 классов, усваивающих материал прямо на уроке.(приложение 1.3.).В 5 классе обучение ведётся в группе высокомотивированных учащихся, поэтому неуспевающих нет. Выше 70% всех учащихся усваивает материал прямо на уроке и только 6%-6 класс, 4,8%-7 класс не усваивает.
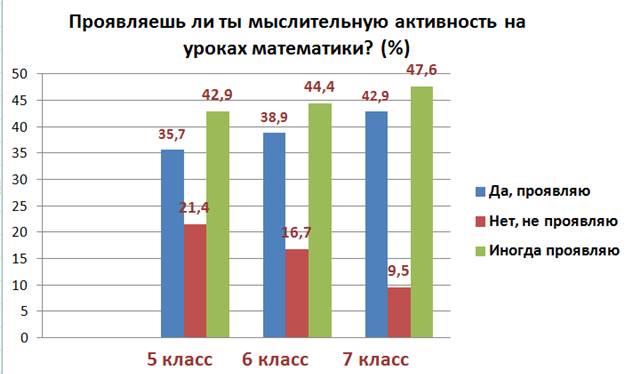
- В результате анкетирования была определена мыслительная активность на уроках математики. Из диаграммы (приложение 1.4) видно, процент обучающихся, проявляющих активность возрастает к 7 классу, что свидетельствует об эффективности применения технологии проблемно-диалогического обучения. Процент учащихся, не проявляющих активность, значительно падает с 5 по 7 класс. Обучающиеся становятся более ориентированные на изучение предмета, проявляются их возрастные особенности.
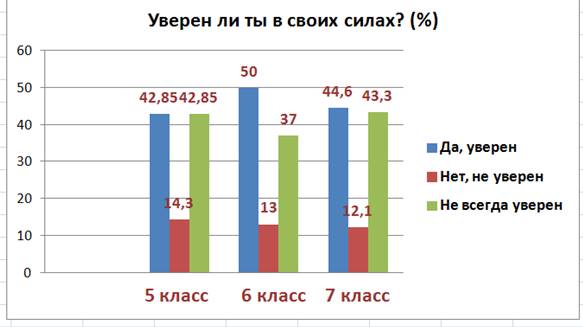
- Анкетирование показало, что преподавание математики с применением технологии проблемно-диалогического обучения позволяет создать для учащихся «ситуацию успеха», так как чуть меньше половины обучающихся утверждают, что уверены в своих силах. Процент неуверенных в себе падает с 14% до 12%. (приложение 1.5)
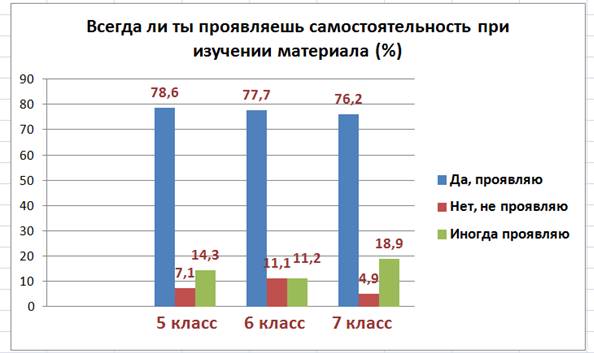
- Анализ результатов анкетирования (приложение 1.6) на выявление самостоятельности учащихся при изучении нового материала показал, что больше 75% обучающихся способны к самостоятельному усвоению материала. Незначительное снижение уровня самостоятельности к 7 классу объясняется усложнением учебного материала, увеличением его объёма. Следовательно, применение технологии проблемно-диалогического обучения формирует самостоятельность учащихся при изучении нового материала.
Таким образом, результаты диагностики подтверждают и доказывают эффективность использования технологии проблемно-диалогического обучения на уроках математики в условиях реализации ФГОС ООО.
ЗАКЛЮЧЕНИЕ
В процессе изучения принципов развивающего обучения, применения его элементов на уроках, я пришла к выводу, что создание проблемных ситуаций в процессе обучения математике позволяет развивать мышление учеников, активизирует их деятельность на уроке, способствует их интеллектуальному развитию, формированию системы универсальных учебных действий учащихся. Цели и задачи технологии проблемно-диалогического обучения полностью соответствуют требованиям ФГОС.
Результаты применения технологии:
-предметные результаты проблемного диалога – качественные знания за счёт познава-тельной мотивации, метода поиска решении – подлинное понимание материала, продук-тивные задания.
Метапредметные результаты:
- Познавательные действия:побуждающий диалог развивает творческие умения осоз-навать и формулировать проблему, выдвигать и проверять гипотезу. Подводящий диалог формирует логические умения сравнивать, анализировать, обобщать. Оба вида диалога и все продуктивные задания развивают речь.
- Коммуникативные действия: работа в парах, группах, школьники учатся слушать друго-го, договариваться, распределять роли.
- Регулятивные действия. Методы постановки проблемы развивают целеполагание. Методы поиска решения учат планированию и контролю, потому что учебное открытие можно спланировать, а открытое знание нужно сверять с учебником.
- Личностные результаты проблемного диалога – становление характера, мотивов, ценнос-тей. Позиция активного деятеля, а не созерцателя воспитывает такие черты характера, как инициативность, смелость, трудолюбие. Роль творца, а не исполнителя усиливает познава-тельную мотивацию учения. Отношения сотрудничества, а не подчинения формируют доброжелательность и уважение к людям.
Преимущества проблемного обучения: это наибольшие возможности для развития внимания, наблюдательности, активизации мышления и познавательной деятельности учащихся, развитие самостоятельности, ответственности, критичности и самокритич-ности, инициативности, нестандартности мышления, осторожности и решительности.
К трудностям проблемного обучения можно отнести то, что на осмысление проб-лемной ситуации и поиски путей решения выхода из нее уходит значительно больше времени, чем при традиционном обучении. Проблемное обучение связано с исследова-нием и поэтому предполагает растянутое во времени решение задачи.
Кроме того, разработка технологии проблемного обучения требует от учителя большого педагогического мастерства и много времени, так как к каждому уроку надо подбирать необходимые и достаточные упражнения для актуализации знаний и создания проблемной ситуации, продумывать постановку проблемы и выбор путей её решения в соответствии с принципом рациональности.
Умение видеть проблемы, задавать вопросы, выдвигать гипотезы, давать определение понятиям проводить наблюдения и эксперименты, делать выводы и умозаключения, класссифицировать и структурировать материал, работать с текстом, доказывать и защи-щать свои идеи - всё вышеперечисленное ведёт к положительному достижению образо-вательных результатов: способности к самостоятельной познавательной деятельности, умению быть успешным в быстроизменяющемся мире и т. д. Использование технологий проблемного обучения позволяет повысить качество образования учащихся.
Практика работы с использованием технологии проблемного диалога показывает, что именно использование разнообразных приемов, методов на различных этапах обучения способствует эффективному формированию познавательной активности и личностных особенностей учащихся.
Так как, технология проблемного диалога направлена на формирование компетенций, необходимых каждому человеку во взрослой жизни, а именно на развитие самопознанияи самовыражения личности, на развитие способности учащихся к самостоятельной работе с информацией любой степени сложности, на формирование у учащихся навыков самообразовании.
Проанализировав свою работу, считаю, что проблемные уроки являются средством повышения эффективности деятельности школьников на уроках математики.
СПИСОК ЛИТЕРАТУРЫ
1. Выступление В.В. Путина на заседании Государственного Совета Российской Федерации 29 августа 2001 г. [Электронный ресурс] – URL: 2002.kremlin.ru›events/284.html
2. Воробьева Е. В. Проблемное обучение как основа профессионального образования на современном этапе // Вестник Иркутского государственного технического университета. - 2007. - № 1. - С. 134-138.
3. Бунеев Р.Н и др. Образовательные технологии. Сборник материалов. –М.: Баласс, 2008.-160с.
4. Крупич В.И. Дидактический механизм возникновения проблемной ситуации в обучении математике. - М.:МГПИ,1984.
5. Кудрявцев Т. В. Проблемное обучение: истоки, сущность, перспективы. - М.: Знание, 1991.
6. Лептина И., Семенова Н. Применение эффективных технологий обучения // Учитель. - 2003. - №1. – С.18.
7. Лернер И.Я. Проблемное обучение. Серия «Педагогика и психология», №7, - М., 1974.
8. Локтионов А. В. Проблемное обучение средствами решения изобретательских задач // Физика в школе. - 2010. - № 3. - С. 49-53.
9. Матюшкин А.М. Психология мышления. Мышление как разрешение проблемных ситуаций. – М.: Книжный дом «Университет», 2009. - 190 с.
10. Махмутов М. И. Организация проблемного обучения в школе. Книга для учителей. - М.: Просвещение, 1977.
11. Махмутов М. И. Проблемное обучение. Основные вопросы теории. - М.: Педагогика,
1975.
12. Мельникова Е. Л. Проблемный урок, или Как открывать знания с учениками: Пособие для учителя. - М., 2002.
13. Оконь В. Основы проблемного обучения. - М.:Просвещение, 1968 г.
14. Педагогическая энциклопедия / Под ред. А. Г. Калашникова [электронный ресурс]. – режим доступа: http://www.nlr.ru/res/inv/cn_old/rosped2.html. Дата обращения 12.12.2016
15. Проблемное обучение на уроках математики .[Электронный ресурс].– Режим доступа: http://festival.1september.ru/articles/211680/ Дата обращения: 13.03.2017 г.
16. Технология проблемного обучения на уроках математики. [Электронный ресурс].– Режим доступа: https://infourok.ru/vistuplenie-na-pedagogicheskom-sovete-tehnologiya-problemnogo-obucheniya-na-urokah-matematiki-570537.html Дата обращения: 16.03.2017
17. Ушинский К. Д. Собрание сочинений [электронный ресурс]. – Режим доступа: http://www.twirpx.com/file/270340/ дата обращения: 12.09.2016 г.
18. Федеральный государственный образовательный стандарт основного общего образования / М-во образования и науки Рос. Федерации. – М.: Просвещение, 2011. – 48 с. – (Стандарты второго поколения).
19. ФурсенкоА.А. О приоритетных направлениях развития образования в Российской Федерации/ М.,2004-с.18.
ПРИЛОЖЕНИЕ 1
Диагностики результатов применения технологии проблемно-диалогического обучения
Приложение 1.1
«Изучение отношения к учению и к учебным предметам» (методика Г.Н. Казанцевой)
Приложение 1.2
АНКЕТА.
1. Всегда ли ты усваиваешь новый материал по математике на уроке?
А) Да, всегда Б) Нет, не всегда В) Частично усваиваю
2. Проявляешь ли ты мыслительную активность на уроках математики при изучении нового материала?
А) Да, проявляю Б) Нет, не проявляю В) Иногда проявляю
3. Уверен ли ты в своих силах, в том, что справишься с учебными заданиями на уроке математики?
А) Да, уверенБ) Нет, не уверенВ) Не всегда уверен
4. Всегда ли ты проявляешь самостоятельность при изучении нового материала на уроках математики?
А) Да, всегда Б) Нет, не всегда В) Иногда проявляю
ПРИЛОЖЕНИЕ 1
Результаты анкетирования
Приложение 1.3
Приложение 1.4
Приложение 1.5
Приложение 1.6
ПРИЛОЖЕНИЕ 2
Дидактические материалы
«Использование проблемных ситуаций на уроке математики в 5-9 классах»
На уроке, проводимом с применением технологии проблемного обучения, можно наблюдать следующие этапы:
1. Мотивация к учебной деятельности
2. Актуализация имеющихся знаний и умений учащихся
3. Создание проблемной ситуации.
4. Построение проекта выхода из затруднения (выдвижение и фиксирование гипотез)
5. Реализация построенного проекта
· исследование, обмен информацией при работе в группах, парах
· представление результатов исследования,
· формулировка выводов, подтверждение или опровержение выдвинутых ранее гипотез
6. Первичное закрепление нового материала с проговариванием во внешней речи
7. Самостоятельная работа с самопроверкой по образцу (или взаимопроверкой)
8. Включение в систему знаний и повторение
9. Рефлексия учебной деятельности
Данная структура урока развивает навыки самостоятельной работы.обеспечивает повышение познавательной активности и мотивации учащихся, формирует умения применять ранее усвоенные знания в новой ситуации, творчески их преобразовывать, способствует развитию интеллектуальных способностей школьников. Создание проблемных ситуаций, их анализ, активное участие учеников в поиске путей решения поставленной учебной проблемы возбуждает мыслительную активность учащихся, поддерживает глубокий познавательный интерес.
На уроках математики использую следующие варианты создания проблемных ситуа-цийчерез:
1) решение задач, связанных с жизнью;
2) умышленно допущенные учителем ошибки;
3) использование занимательных задач (5-6 классы);
4) решение задач на внимание и сравнение (5-6 классы);
5) различные способы решения одной задачи;
6) выполнение небольших исследовательских заданий (7-8 классы).
Побуждающий от проблемной ситуации диалог.
|
Приёмы создания проблемной ситуации |
Побуждение к осознанию противоречия |
Побуждение к формулированию проблемы |
|
1. Одновременно предъявить противоречивые факты, теории, точки зрения |
О фактах: - Что вас удивило? Что интересного заметили? Какие вы видите факты? О теориях: - Что вас удивило? Сколько существует теорий (точек зрения)? |
Выбрать подходящее: - Какой возникает вопрос? - Какова будет тема урока?
|
|
2. Столкнуть мнения учеников вопросом или практическим заданием |
- Сколько в классе мнений? Почему так получилось? |
|
|
3. Шаг 1. Выявить житейское представление учащихся вопро-сом или практическим заданием «на ошибку». Шаг 2. Предъявить научный факт сообщением, экспери-ментом, наглядностью. |
- Вы сначала как думали? - А как на самом деле? |
|
|
4. Дать практическое задание, не сходное с предыдущими заданиями. |
- Вы смогли выполнить задание? Почему не получается? Чем это задание не похоже на предыдущие задания? |
|
|
5. Шаг 1. Дать практическое задание, сходное с предыдущи-ми заданиями. Шаг 2. Доказать, что задание учениками не выполнено. |
- Что вы хотели сказать? Какие знания применили? Задание выполнено? |
1) Создание проблемных ситуаций через умышленно допущенные учителем ошибки.
Задачи с заведомо допущенными ошибками. Данный приём развивает внимание, активизирует мыслительную деятельность учащихся. В понимании детей учитель – это компьютер, который не может ошибиться никогда, и они обычно слепо копируют его решение. Иногда учителю полезно предложить “найти ошибки” в заданиях, которые выполнены верно. Чтобы проанализировать готовое решение, детям необходимо сначала самим правильно решить задачу. Проанализировав, сравнив, приходят к выводу, что решение верное. Но бывает, что ребёнок сам допускает ошибку. Возникает проблемная ситуация. Тогда на помощь приходит класс или учитель.
Урок алгебры 7 класс тема «Формулы сокращённого умножения»
При изучении темы учитель предлагает ученикам решить ряд примеров, ранее известным им способом умножением многочлена на многочлен. Одновременно с учениками учитель решает эти примеры, записывая решение так, чтобы ученики не видели, а затем предлагает проверить решение и записи.
|
Запись учеников |
Запись учителя |
|
а) (3-а)(3+а) = 9+ 3а – 3а – а2 = 9 - а2 б) (5с-6)(5с+6)= 25с2 + 30с – 30с - 36 =25с2 - 36 в) (8+ 3у)(8 – 3у)= 64 – 24у +24у – 9у2 = 64 - 9у2; |
а) (3-а)(3+а) = 9 - а2 б) (5с-6)(5с+6)= 25с2 - 36 в) (8+ 3у)(8 – 3у)= 64 - 9у2; |
Ученики, сравнивая ответы и записи решений, видят, что задания решены учителем правильно и запись решения, сделанная учителем короче, но при этом ответы одинаковые. И тут учитель предлагает учащимся найти некоторые закономерности, которые потом формулируются в правило. Особое внимание учеников при изучении темы «Формулы сокращённого умножения» обращается на то, что знание формул широко используется в заданиях ЕГЭ и ГИА.
6 класс.Тема «Линейные уравнения с одной переменной»
Решаю быстро уравнение:
(3х + 7) × 2 – 3 = 17
6х + 14 – 3 = 17
6х = 17 – 14 – 3
6х = 0
х = 0 (При проверке ответ не сходится. Проблемная ситуация. Ищем ошибку. Дети решают проблему)
2) Создание проблемной ситуации на основе постановки предварительных заданий на уроке к материалу учебника.
Такие задания ставятся перед учащимися до изучения нового материала или в начале объяснения нового материала.
5 класс. Тема Числовые и буквенные выражения»
Изучение новой темы начинается с постановки вопроса:
На экране записаны выражения:
35 + 47; 87 – y; 89 + b; 234 – 33; y + b; 61 – 18;
- Ребята, внимательно посмотрите, на какие две группы можно разделить эти выражения? Попросить записать их в два столбика:
35 + 47; 87– y;
234 – 33; 89 + b;
61 – 18; y + b;
- почему вы пришли к такому разделению?
- дайте название каждому столбику (числовые и буквенные).
- сформулируйте тему сегодняшнего урока.
- «Числовые и буквенные выражения»
- Сегодня мы будем учиться читать и записывать буквенные выражения.
Такая работа требует логического анализа материала, активизирует внимание и мыслительную деятельность, делает восприятие материала более целенаправленным.
6 класс. Тема«Признаки делимости чисел на 10, на 5 и на 2»( для сильного класса)
Для решения проблемной ситуации учащимся необходимо было выдвинуть гипотезу, проверить её и сформулировать выводы.
На доске (экране) записаны числа:1 289 565, 246 560, 24, 188 536, 1873. Предлагаю учащимся, не производя деления, из предложенных чисел, найти те, которые делятся на 10, на 5 и на 2.
Затем предлагаю самостоятельно написать несколько многозначных чисел, делимость которых на 10, на 5 и на 2 они могут предугадать.
После того как, учащиеся выполнят эту работу, я предлагаю им попытаться найти признаки делимости чисел на 10, на 5 и на 2.
После того как учащиеся попытаются сформулировать признаки, предлагаю им высказать своё мнение: стоит ли этим заниматься? Не проще ли разделить?
После высказывания предположений ученики проверяют их непосредственным делением. Затем организуется сопоставление с учебником, и формулируются окончательные выводы, которые записываются в форме таблицы:
|
Признаки делимости натуральных чисел |
|||
|
Если оканчиваются |
на 10 |
на 5 |
на 2 |
|
0 |
0 или 5 |
0; 2; 4;5; 6 ;8 |
|
3) Создание проблемных ситуаций через решение задач, связанных с жизнью.
Здесь происходит сталкивание противоречий теоретических знаний и практической деятельности.
Школьникам предлагается выполнить такое задание, для выполнения которого у них недостаточно знаний, нужно ещё что-то новое узнать, изучить. Такие задания стимулируют познавательную деятельность, дети понимают, что выполнить его можно только после определённой теоретической подготовки. Противоречие между теоретическими знаниями и практической деятельностью приводит к проблемной ситуации, а в конечном итоге, к активизации познавательной деятельности.
5 класс. Тема урока: Периметр прямоугольника.
Семья Кости летом переехала в новый дом. Им отвели земельный участок прямоугольной формы. Папа решил поставить изгородь. Он попросил Костю сосчитать, сколько потребуется штакетника, для изгороди, если на 1 погонный метр изгороди требуется 10 штук? Сколько денег потратит семья, если каждый десяток стоит 100 рублей.
Сразу же начинается обсуждение задачи: Какой Костя? На какой улице его дом? Косте нужно помочь. Но как? Возникает затруднение. Придётся нам решать эту проблему. Проблемная ситуация создана.
Для её решения высказываются ребятами различные предположения (может, сходим на место и попробуем прикладывать по всей длине огорода рейки, но это очень долго; можно спросить у старших дома; может, сами попробуем найти в учебнике какое-то решение и т.д.).Вместе выдвигаеми формулируем основную гипотезу: «нужно найти периметр прямоугольника, он и будет длиной изгороди». Записываем формулу, используем её на практике. Затем делаем вывод: формула периметра прямоугольника нужна. Доводим решение задачи до конца: Косте помогли!
5 класс. Тема урока «Объём прямоугольного параллелепипеда»
Задача №1.Длина аквариума 80 см, ширина 45 см, а высота 55 см. Сколько воды надо влить в этот аквариум, чтобы уровень воды был ниже верхнего края аквариума на 10 см?
Проблема: не знают понятие объема и формулу для нахождения объема параллелепипеда.
Учащиеся выбирают необходимую им информацию, используя текст учебника. Обсуждают решение задачи, делают вывод, записывают формулу в тетради.
Задача №2.Длина плавательного бассейна 200 м, а ширина 50 м. В бассейн налили 2 000 000 л воды. Можно ли плыть в этом бассейне?
Проблема: несоответствие единиц измерения.
Учащиеся ищут пути решения задачи, используя повествование учителя о единицах измерения объемов.
Урок математики 5 класс «Задачи на проценты».
|
Учитель |
Ученики |
|
- Предположим, что сначала цена товара была равна А. Затем цена повысилась на 10%, а в новом году снизилась на 10%. Изменилась ли первоначальная цена дтовара? (Вопрос на ошибку) - Давайте посчитаем. Цена товара была 4000 руб. После повышения на 10% цена стала 4400 руб. А после понижения на 10% стала 3960 руб. (предъявление научного факта). - Итак, что вы сказали сначала? - А что оказывается на самом деле? (Побуждение к осознанию противоречия.) - Какой же сегодня будет тема урока? (Побуждение к формулированию проблемы.) |
- Цена товара не изменилась (житейское представление).
- Испытывают удивление (возникновение проблемной ситуации).
- Что цена не изменится. - Цена уменьшилась (осознание противоречия). - Задачи на проценты (учебная проблема как тема урока). |
Здесь происходит сталкивание противоречий теоретических знаний и практической деятельности.Школьникам предлагается выполнить такое задание, для выполнения которого у них недостаточно знаний, нужно ещё что-то новое узнать, изучить. Такие задания стимулируют познавательную деятельность, дети понимают, что выполнить его можно только после определённой теоретической подготовки. Противоречие между теоретическими знаниями и практической деятельностью приводит к проблемной ситуации, а в конечном итоге, к активизации познавательной деятельности.
4) Создание проблемных ситуаций через использование игровых ситуаций и занимательных задач
Игровая ситуация «Математические предсказания»
Алгебра 7 класс Тема: «Формулы сокращенного умножения»
Предлагаю ученикам придумать задания на возведение в квадрат разности или суммы двух выражений, произведения суммы и разности двух выражений. Предложенные задания решаются учениками на доске с применением правила умножения многочленов. Учитель выступает в роли предсказателя ответов придуманных заданий: не глядя на доску, предсказывает будущие ответы. Результаты учеников и «предсказания» учителя прописываются на доску. Ответы действительно одинаковые. Ученики удивлены. В результате решения проблемной ситуации, выясняется, что секрет данного математического фокуса кроется в формулах сокращенного умножения.
Алгебра 7 класс. Тема: «Линейная функция»
Обычная форма задания.Функция задана формулой y = x + 2. Найдите значение функции
при x = 0, 6, -3, 8, 1.
Занимательная форма задания. Приглашаю к доске ученика, даю ему карточку, на которой
написано y = x + 2. На доске заготовлена таблица:
|
x |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
Один ученик из класса называет какое-нибудь значение x. Ученик у доски вписывает это
число в таблицу и, поставив его в формулу, находит и вписывает в таблицу соответствующее
ему значение y. Затем другой ученик из класса называет другое значение x и ученик у доски
проделывает те же операции. Возникаетпроблема: “Угадать” формулу, записанную на
карточке. Проблемная ситуация создана. Гипотеза: для того чтобы угадать формулу, надо
найти какую-то закономерность. Продолжаем подставлять значения x и находим
закономерность, и делаем вывод: зная закономерность, легко угадать формулу. В итоге
выигрывает тот ученик, который первый назовет формулу.
Алгебра 9 класс Тема «Сумма n-первых членов арифметической прогрессии»
Изучение вопроса о сумме n–первых членах арифметической прогрессии в 9-ом классе начинаю с рассказа: «Примерно 200 лет тому назад в одной из школ Германии на уроке математики учитель предложил ученикам найти сумму первых 100 натуральных чисел. Все принялись подряд складывать числа, а один ученик почти сразу же дал правильный ответ».
Имя этого ученика Карл Фридрих Гаусс. В последствии он стал великим математиком. Как удалось Гауссу так быстро подсчитать эту сумму
Проблемная ситуация: Как найти быстро сумму первых 100 натуральных чисел?
Решение проблемы (1 + 100) · 50 = 5050
Последовательность чисел 1, 2, 3,…,100 является арифметической прогрессией. Теперь выводим формулу суммы n-первых членов арифметической прогрессии.
Главный фактор занимательности – это приобщение учащихся к творческому поиску, активизация их самостоятельной исследовательской деятельности, так как уникальность занимательной задачи служит мотивом к учебной деятельности, развивая и тренируя мышление вообще и творческое, в частности.
Эффективным средством создания проблемных ситуаций является использование стихов, ребусов, сказок, басен и других занимательных приёмов.
5) Создание проблемных ситуаций через решение задач на внимание и сравнение.
Геометрия 7 класс Тема: «Сумма углов треугольника»
Учитель читает условие задачи, ученики анализируют его и выявляют ошибки, тем самым мы можем проверить учеников на внимательность. В данных задачах следует вспомнить теорему о сумме углов треугольника, полагаясь на данную теорему, мы придем к выводу, что не все условия задач поставлены корректно, тем самым некоторые треугольники не существуют.
Задание 1. Построить треугольник по трем заданным
углам
![]()
![]()
![]()
![]()
Учащиеся, вооружившись линейкой и транспортиром, начинают строить треугольники. По окончании уже можно выдвинуть предположение о сумме внутренних углов треугольника. Здесь уместен провокационный вопрос: «В каком треугольнике, по вашему мнению, сумма внутренних углов больше, в остроугольном или тупоугольном?» Практика показывает, что в каждом классе найдутся несколько человек, которые, зная, что тупой угол всегда больше острого, по анальгии скажут, что сумма внутренних углов тупоугольного треугольника, больше, чем остроугольного. Я предлагаю им на практике проверить свое утверждение.
Задание 2. Два угла треугольника равны 134º и 46º. Найти величину третьего угла.
Задание 3.Дан треугольник АВС, где ![]() . Найти
. Найти ![]() .
.
6) Создание проблемных ситуаций через противоречие нового материала старому, уже известному.
Здесь учитель должен подвести школьников к противоречию, вызывающему у них
удивление или затруднение. Этот путь наиболее сложен, так как он в точности повторяет
звено постановки проблемы в настоящем научном творчестве. Однако именно таким
образом формируется творческая способность учащихся к самостоятельному осознанию
противоречия и формулированию проблемы.
Алгебра 7 класс. Тема: «Формулы сокращённого умножения»
Учитель дает задание, пытаясь запутать учеников. Вычислите:
(3٠4)2 =32٠42=9٠16=144
(5٠6)2 =52٠62=25٠36=900
(8:2)2 =82:22=64:4=16
(3:9)2 =32:92= ![]() =
= ![]()
(5+6)2 =52+62=25+36=61
Решим последний пример, соблюдая порядок действий в вычислениях: (5+6)2 =112=121
Имеем: (5+6)2≠52+62
Почему в итоге получились разные результаты? И какой из результатов верный?
Ученики обращают внимание на знак в последнем примере и понимают, что данный пример решается по-другому (применяя формулу для квадрата суммы).
Урок математики 5 класс «Умножение десятичных дробей на натуральные
числа».
|
Учитель |
Ученик |
|
Домашнее задание у вас было записать количество расходов (в рублях и копейках), которые производит ваша семья, оплачивая коммунальные платежи, а для электроэнергии, записать показания счётчика за месяц и стоимость 1 квт/ч. Сейчас я предлагаю вам подсчитать, сколько в среднем семья тратит на оплату коммунальных услуг. Задание. Сумма всех платежей составила: 1)Содержание жилья, вывоз мусора, обслуживание – 775,37 руб. 2)Холодная вода, водоотведение – 660,77 руб. 3)Горячая вода, отопление – 3 062,42 руб. 4)Электроэнергия – 85 киловатт (1 киловатт стоит 3,66 рубля). Итого: ? рублей. |
Поиск и выделение необ-ходимой информации, выска-зывают свои предположения. Учащиеся предлагают всё сложить, но замечают, что нап-ротив электроэнергии нет конкретного числа. (Возникает проблемная ситуация)
|
|
- Ребята! Как вы думаете, что же нам надо сделать?
- Умеем ли мы вычислять такое произведение? |
- Надо вычислить произведение десятичной дроби и натураль-ного числа. - Нет. |
|
- Как вы думаете, какая же тема нашего урока? |
- Умножение десятичных дробей на натуральные числа |
Проблемный характер изложения учебного материала, организация поисковой, познавательной деятельности учащихся, даёт им возможность переживать радость самостоятельных открытий, формирует универсальные учебные действия.
7) Познавательные задачи.
Огромное значение для активизации познавательной деятельности имеют познавательные задачи. Если ученик воспринимает задачу как проблему и самостоятельно ее решает, то это есть главнейшее условие развития его мыслительных способностей.
Типология задач.
1. Задачи с несформулированным вопросом.
Пример. Шоколад стоит 45 руб., коробка конфет 180 руб. Задайте все возможные вопросы по условию данной задачи.
2. Задачи с недостающими данными.
Пример. Из двух пунктов вышли одновременно навстречу друг другу два пешехода. Скорость одного пешехода равна 6 км/ч, а скорость другого – на 1 км/ч больше. Какое расстояние будет между пешеходами через 2 часа?
Учащимся задаются вопросы:
-Почему нельзя дать ответ на вопрос задачи?
- Чего не хватает?
- Что нужно добавить?
- Докажи, что теперь задачу точно можно будет решить?
- А можно ли что-нибудь извлечь даже из имеющихся данных?
- Какое заключение можно сделать из анализа того, что дано?
3. Задачи с излишними данными.
Пример.Масса 11 ящиков яблок 4 ц 62 кг, а масса 18 ящиков груш 6 ц 12 кг. В магазин привезли 22 ящика яблок и 6 ящиков груш. На сколько килограммов масса одного ящика яблок больше массы одного ящика груш.
4. Задачи с несколькими решениями.
Пример. За три дня в магазине продано 1280 кг яблок. В первый день продали 25% всех яблок, а во второй день – 45% всех яблок. Сколько килограммов яблок продали в третий день? Решите задачу несколькими способами. Какой из них наиболее простой.
5. Задачи с меняющимся содержанием.
Пример. Исходная задача. Туристы прошли за день 20 км, что составило 40% намеченного маршрута. Какова длина маршрута?
Второй вариант. Туристы прошли за день 20 км, и им осталось пройти 60% намеченного маршрута. Какова длина маршрута?
6. Задачи на соображение, логическое рассуждение.
В заключении можно сказать, что использование проблемных ситуаций на уроках:
· прежде всего формирует регулятивные универсальные учебные действия, обеспечивая выращивание умения решать проблемы. Наряду с этим происходит формирование и других универсальных учебных действий: за счёт использования диалога – коммуникативных, необходимости извлекать информацию, делать логические выводы и т.п. – познавательных.
· Ребята больше думают, чаще говорят, активнее формируют мышление и речь и им очень нравится, что они сами могут объяснить увиденные явления, опыты, формулы. Это мотивирует школьников к усвоению нового материала, включая в работу практически весь класс. Диалогический поиск решения, в отличие от изложенных готовых сведений, обеспечивает понимание нового знания каждым учеником. Они учатся отстаивать собственную позицию, рискуют, проявляют инициативу.
ПРИЛОЖЕНИЕ 3
Конспект урока по теме
«Деление с остатком» (урок 1)
Автор: Бисева Ольга Сергеевна, учитель математики.
Тема учебного раздела: Натуральные числа.
Продолжительность: 45 минут.
Предмет, класс, в котором используется продукт: математика, 5 класс.
Авторы учебника, учебно-методического комплекта: Н.Я. Виленкин, В.И.Жохов, А.С. Чесноков, С.И. Шварцбурд. Математика 5 класс.
Тип урока: урок изучения и первичного закрепления знаний по теме «Деление с остатком».
Формы организации труда: индивидуальная, групповая, фронтальная.
Методы обучения: словесный, наглядный, проблемный, практический.
Оборудование: интерактивная доска, проектор, компьютер.
Пояснительная записка: при подготовке урока в 5 классе я руководствовалась возрастными особенностями учащихся и государственным стандартом по математике.
Цели урока
1. Образовательные:
- учить выполнять деление с остатком, записывать его в виде формулы а= сb + d, где а -делимое, с –неполное
частное,b- делитель и d- остаток;
- учить находить неизвестные компоненты данной формулы по известным другим.
2. Воспитательные:
- воспитывать уверенность в себе, мотивацию к обучению, чувство ответственности за командный успех.
3. Развивающие:
- способствовать развитию познавательного интереса к изучаемому предмету.
Здоровье сберегающий аспект урока:
- доброжелательная атмосфера, способствующая положительному эмоциональному настрою;
- создание ситуации успеха на уроке;
- чёткая организация урока;
- подвижная физкультминутка для снятия усталости.
План урока .
1. Организационный момент. (проверка готовности к уроку) ( 1 мин)
2. Актуализация опорных знаний. Устный счёт.( 5 мин)
3. Математический диктант. (5 мин.)
4. Изучение нового материала. ( 6 мин.)
а) Постановка проблемной ситуации
б) Решение проблемной ситуации
5. Физкультминутка. ( 1 мин)
6. Первичное закрепление нового материала. ( 5 мин)
7. Решение задач.(10 мин)
8. Повторение. (7 мин)
9. Домашнее задание. (2 мин)
10. Итоги урока. Рефлексия.( 3 мин)
ХАРАКТЕРИСТИКА УРОКА
|
Техноло-гии, приме-няемые на уроке |
Решаемые проблемы |
Виды деятельности (элементы содержания, контроль) |
Планируемые результаты |
||
|
предметные |
УУД |
личностные |
|||
|
Проблем-ного обучения.
|
Что нового узнали о деление с остатком? Как называются компоненты деления с остатком? |
Математический диктант, устная работа, работа с текстом учебника, работа у доски, фронтальная работа с классом. |
ПРЕДМЕТНЫЕ Знать: - названия компонентов деле-ния с остатком; - правило нахождения делимого при делении с остатком. Уметь: - выполнять деление с остатком; - находить неизвестные компоненты действий деления и умножения. |
Коммуникативные: уметь точно и грамотно выражать свои мысли; уметь слушать других. Регулятивные: работать по составленному плану, формировать целевые установки учебной деятельности, выстраивать алгоритм действий. Познавательные: осуществлять поиск необходимой информации для выполнения учебных заданий. |
Формирование познавательно-го интереса к изучению нового. |
|
№ стр. |
Этап урока, страницы флипчарта |
Действия учителя (ДУ) Формы организации работы учителя
|
Действия учащихся,
|
Формы организа-ции их работы |
|
2 |
1. Организационный этап. (проверка готовности к уроку)
|
- Здравствуйте! Садитесь! Посмотрите, всё в порядке Ручки, книжки и тетрадки. Все готовы вычислять, и делить и умножать? Все готовы? ДУ:обращает внимание на доску. -Найдите закономерность и вставьте пропущенное число? (Учащимся даётся задание на развитие высших психических функций (мышление, внимание), с целью подготовить мыслительную деятельность обучающихся к активной работе на уроке) ДУ:акцентирует внимание учащихся на действие, которым было найдено число. Работа со страницей наИД: нажимает на знак вопроса, появляется число 9. - На прошлых уроках мы с вами изучали тему «Деление». - Сегодня мы продолжим изучение этой темы. Работа со страницей наИД: нажимает на синюю стрелку справа (осуществляется переход на другую страницу). |
Ответы детей.(Да)
Думают над заданием.
Учащиеся замечают, чтобы найти пропущенное число нужно 36:4.
Внимательно слушают учителя.
|
Фронталь-ная работа |
|
3
4 |
2. Закрепление ранее изученного материала. Устный счёт.
Фронтальная устная работа + математический диктант (8)
|
- Давайте, ребята, учиться считать: Делить, умножать, прибавлять, вычитать. Запомните все, что без устного счёта Не сдвинется с места любая работа. На уроке у нас сегодня в гостях Волк и Заяц из знакомого всем мультфильма «Ну погоди!». - Раскрасьте картинку на доске. - Перед вами примеры и три варианта ответов, из которых один верный, если выберите верный ответ, то часть картинки закрасится, а если нет, то ответ пропадает. ДУ:вызывает детей по очереди к доске.
Работа со страницей наИД: нажимает на синюю стрелку справа (осуществляется переход на другую страницу).
ДУ:предлагает учащимся устно дать ответы на предложенные на доске вопросы.
- Определите сколько цифр в частном: 7416:36; - Выполните деление: 55: 5 3606: 6 - Сравните числа 28 и 7
9 и 63
- Каким действием определяется во сколько раз одно число больше или меньше другого? - 160 кг картошки разложили в 4 мешка поровну. Сколько кг картошки в одном мешке? Работа со страницей на ИД: С помощью инструмента «Выбор» нажимает по зелёным кнопкам 1, 2, 3, 4,5,6,7,8, в "облачках" появляются задания. После устного разбора проверяем свой ответ, произведя щелчок по соответствующей салатовой кнопке, расположенной вверху кнопок соответственно. - Запишите число, классная работа, математический диктант. Цифра 8 (математический диктант с проверкой) ДУ: читает задания. 1) Определите сколько цифр будет в частном и выполните деление: 808:3 312: 3 7585: 37 2) а) Во сколько раз число 60 больше числа 5? б) Во сколько раз число 4 меньше числа 100? Работа со страницей на ИД: С помощью инструмента «Выбор» нажимает на салатовую кнопку над цифрой 8 , появляется ответы на доске. - нажимает на синюю стрелку справа (осуществляется переход на другую страницу). |
Решают у доски по очереди примеры, остальные внимательно слушают друг друга.
Работа со страницей на ИД: С помощью инструмента «Выбор» нажимают на ответ, если он выбран верно, то часть картинки закрашивается, а если нет , то выбранное число пропадает.
Отвечают устно на вопросы, записанные на доске. - Три. - 11. - 101. - 28 больше 7 в 4 раза. - 9 меньше 63 в 7 раз
- делением.
-40.
Делают необходимые записи в тетради.
Внимательно слушают учителя и пишут математический диктант в тетрадях.
Меняются тетрадями. Осуществляют взаимопроверку. |
Работа у доски.
Фронталь-ная устная работа
Индиви-дуальная работа.
|
|
5
6 |
3. Изучение нового материала.
а) Постановка проблемной ситуации
б) Решение проблемной ситуации
|
Работа со страницей на ИД: С помощью инструмента «Выбор» нажимает на прямоугольник, появляется условие задачи. - Перед вами проблемная задача: У девочки есть 30 рублей, ей нужно купить булочки. Цена одной булочки 10 рублей. Какое максимальное количество булочек она может купить?
Работа со страницей на ИД: С помощью инструмента «Выбор» нажимает на монеты появляется другое условие задачи.
- На следующий день у девочки также 30 рублей, но булочка стоит уже 12 рублей, сколько булочек теперь может купить девочка? Работа со страницей наИД: нажимает на синюю стрелку справа (осуществляется переход на другую страницу). - Чтобы ответить на вопрос задачи нужно 30 : 12, но 30 на 12 не делится на цело, а только с остатком. - Запишите тему нашего урока «Деление с остатком» и запишем деление «уголком» 30: 12
- Как называются компоненты при делении с остатком? ДУ: указывает на число 30, затем 12, 6 и 2. Работа со страницей на ИД: С помощью инструмента «Выбор» кликает на число в делении уголком, появляются названия компонентов деления. - Сравните остаток с делителем, что можно про них сказать? - Как можно проверить правильно ли выполнено деление? Объясните. - Проверим правильность наших выводов. Работа со страницей на ИД: С помощью инструмента «Выбор» кликает на изображение «Зайца», появляется задание для учащихся.
- Откройте учебник на стр. 81. - Прочитайте статью и приготовьтесь отвечать на вопросы. - Может ли остаток быть больше делителя? - Может ли он быть равен делителю? -Как найти делимое по неполному частному, делителю и остатку? |
Внимательно слушают.
Перед учащимися создаётся проблемная ситуация с помощью которой реализуются принципы продуктивной обработки информации и развития мотивации.
Предлагают свои ответы.( 3булочки)
Предлагают решение проблемы.(2 бул.)
Выполняют деление уголком в тетрадях и подписывают компоненты деления
Отвечают на вопрос. -Остаток меньше делителя. - Умножением делителя и неполного частного с добавлением остатка.
- нет. - да, тогда число делится нацело. -Неполное частное умножить на делитель и прибавить остаток. |
Фронталь-ная работа
Работа в тетрадях.
Работа по учебнику. (индивид.) |
|
7 |
Физкультминутка.
|
Физкультминутка. Работа со страницей на ИД: кликает по левой руке Волка, а затем включает звукозапись.
Закройте глаза и представьте, что ваш нос вырос, как у Буратино. Обмакните его, как в сказке, в чернила и напишите как можно красивее носом воздухе слово делимое, сделайте это с движением головы; зафиксируйте слово перед глазами. |
выполняют движения. |
|
|
8
|
4. Первичное закрепление нового материала.
|
- Помогите Зайцу найти и исправить ошибки, которые допустил Волк в вычислениях. ДУ:вызывает ученика к доске (или по желанию по очереди несколько учащихся).
Работа со страницей наИД: нажимает на синюю стрелку справа (осуществляется переход на другую страницу).
|
(остальные записывают все примеры себе в тетрадь)
Работа со страницей на ИД: С помощью инструмента «Перо» ученик исправляет ошибки, если требуется производит вычисления на стикере, на который наложено действие «перетащить копию»
|
Индиви-дуальная работа у доски.
|
|
9 |
|
-Сформулируйте условия деления с остатком, запишите их себе в тетрадь. - Сформулируйте правило нахождения делимого по неполному частному и остатку, запишите правило в тетрадь.
. Работа со страницей на ИД: - кликает по цифрам 1,2., затем щёлкнув на знак восклицания откроется правило, кликая на буквы которого открывается их обозначение внизу страницы; - нажимает на синюю стрелку справа (осуществляется переход на другую страницу).
|
Формулируют условия, затем записывают с доски их себе в тетрадь. - Остаток должен быть меньше делителя. -Если неполное частное умножить на делитель и прибавить остаток, то получится делимое. a=c×b +d, где а- делимое, с- неполное частное, b- делитель и d- остаток. |
Фронталь-ная работа.
Работа в тетрадях.
|
|
10 |
5. Решение задач.
|
- Откройте учебник на странице 82 № 533 (а,б,е,ж)
а- решаем у доски с объяснениями . б- решаем самостоятельно, затем проверяем вместе. е – решаем у доски с объяснениями ж- решаем самостоятельно, затем проверяем.
Работа со страницей на ИД: произведя щелчок по "Зайцу" - производим проверку решения. После выполнения номера нажимает на синюю стрелку справа (осуществляется переход на другую страницу).
|
а- выполняет 1 ученик у доски, остальные в тетрадях. б- самостоятельно решают, затем 1 человек показывает решение на доске. е- выполняет 1 ученик у доски, остальные в тетрадях. ж- самостоятельно решают, затем 1 человек показывает решение на доске. Работа со страницей на ИД: Ученик записывает решение у доски, используя инструмент «Перо» в нижнем углу прямоугольника. (а класс записывает при этом все в тетради). |
Работа у доски. Самос-тоятельнаяработа.
|
|
11 |
|
- № 534. ДУ: даёт инструкцию по выполнению задания.
Работа со страницей на ИД: После выполнения номера нажимает на синюю стрелку справа (осуществляется переход на другую страницу).
|
Выполняют задание. Работа со страницей на ИД: На цифры внизу страницы наложено действие "Перетащить копию". Ученики по очереди ( по желанию или можно использовать двухпользовательский режим) выходят к доске и с помощью инструмента "Выбор" помещают нужные остатки в прямоугольники, остальные выполняют номер в тетрадях. |
|
|
12 |
|
- Прочитайте задачу. ДУ: обсуждает с классом задачу, задаёт вопросы.
Работа со страницей на ИД: После решения задачи щелкает по "Зайцу" - производим проверку решения.
|
Самостоятельно записывают решение в тетради и производят вычисления. 400:13=30 (ост.10) 400=30·13+10 |
Работа в тетрадях. |
|
13 |
7. Повторение.
|
- Прежде чем вспомнить материал, который мы изучали на предыдущих уроках, давайте разделимся на две команды: команду Волка, команду Зайца. ДУ:делит класс на команды ( 1 вариант- команда Зайца, 2 вариант – команда Волка)
Работа со страницей на ИД: включает звукозапись, если требуется пока дети рассаживаются по командам. |
Рассаживаются по группам. |
|
|
14 |
|
- Кто больше поймает мячей? ДУ:инструктаж по выполнению задания.
Работа со страницей на ИД: Производит щелчок по нужной картинке (Волка или Зайца), затем по номеру задания напротив этой картинки при этом появляется задание и два варианта ответов (для того чтоб появились нажимаем на цифры 1 и 2 около открытого задания), один из которых верный.
Работа со страницей на ИД: После выполнения номера нажимает на синюю стрелку справа (осуществляется переход на другую страницу).
|
Внимательно слушают пояснения учителя. Каждой команде предлагается по 3 задания ( напротив картинок Волка и Зайца). По жребию начинает одна из команд. Работа со страницей на ИД: Ученик из команды пишет пером на стикере, затем выбирает ответ и производит по нему щелчок. Если выбран верный ответ, то команде прибавляется мяч, если же выбран неверный ответ, то появляется в ячейке вместо мяча крестик. На кнопку с решенной задачей накладывается "накладка", поэтому команда не может выбрать одну и туже задачу дважды. Побеждает команда набравшая большее количество мячей (максимум три, они собираются в урнах у Волка и Зайца справа). |
Работа в группах.
|
|
15
15 |
|
ДУ: объясняет задание, вызывает по человеку от каждой команды.
ДУ: считает верные ответы и прибавляет мячи командам.
|
По ученику от команд работают у доски, остальные в тетради.
Работа со страницей на ИД: Двухпользовательский режим. На мел у каждой доски наложено дествие "Перо", решают уравнения, затем с помощью инструмента "Лупа" проверяют ответ (прямоугольник в левом нижнем углу каждой доски).
|
|
|
16 |
9. Домашнее задание.
|
Работа со страницей на ИД Учитель кликает "домик" , открывается домашнее задание.
- пункт 13 стр. 81, № 550 (а,б), № 552, № 556 (а). |
Открывают дневники, записывают домашнее задание.
пункт 13 стр. 81, № 550 (а,б), № 552, № 556 (а). |
|
|
17 |
8. Итог урока.
|
ДУ: подводит итог урока, выставляет оценки.
Работа со страницей на ИД Учитель выдвигает бегущего "Зайца" вправо и задаёт вопросы классу. |
Отвечают на вопросы, решают задачи на деление с остатком из жизни.
Акцентируется внимание на трудных моментах в теме, связь математики с жизнью. |
|
|
18 |
10. Рефлексия.
|
- Перед вами на доске три квадрата: Зелёный – обозначает….. Жёлтый - ….. Красный….. (читает на доске) - подойдите по очереди к доске и выберите один из квадратико
Работа со страницей на ИД Учитель кликает на квадратики слева по очереди , открывается их обозначение.
-- СПАСИБО ЗА УРОК! |
Внимательно слушают учителя
Работа со страницей на ИД С помощью инструмента «выбор» производят щелчок по выбранному квадратику справа в нижнем углу. ( на каждый квадрат наложено действие «Растяжение вверх») |
|
ПРИЛОЖЕНИЕ 4
Конспект урока по геометрии 7 класс.
Тема урока: «Некоторые свойства прямоугольных треугольников»
Тип урока: Урок открытия и первичного закрепления новых знаний
Цель урока: Создать условия для освоения основных понятий: равнобедренный треугольник, прямоугольный треугольник; формулирования и доказательства свойств прямоугольных реугольников; организовать деятельность обучающихся по восприятию, осмыслению и первичному закреплению новых знаний и способов деятельности.
Задачи:
Образовательные (формирование познавательных УУД): помочь учащимся «открыть» некоторые свойства прямоугольных треугольников, формировать умение применять их при решении задач базового уровня
Развивающие (формирование регулятивных УУД): развивать логическое мышление и навыки исследовательской работы, формировать умение анализировать, выдвигать гипотезы, переносить свои знания в новые ситуации, тренировать память и математическую речь, побуждать к любознательности;
Воспитательные (формирование коммуникативных и личностных УУД): воспитывать сознательное отношение к учебному труду, развивать интерес к математике, самостоятельность, прививать аккуратность и трудолюбие.
Методы и приёмы обучения:
По способу приобретенных знаний – словесные (диалог), наглядные, практическая работа;
По уровню познавательной активности - проблемный, самостоятельная работа, коллективное обучение, решение познавательных задач.
Формы работы : фронтальная, индивидуальная , работа в парах.
Планируемые результаты обучения:
Предметные: умение измерять углы треугольника и его стороны; умение делать выводы на основе полученных результатов (свойства прямоугольного треугольника); умение применять свойства прямоугольного треугольника к решению задач.
Метапредметные:
-регулятивные УУД: развивать умение ставить перед собой цель - целеполагание; планировать свою работу - планирование; уметь контролировать и оценивать собственную деятельность и деятельность своих товарищей;
-коммуникативные УУД: умение работать в парах и группе, обсуждать свойства прямоугольных треугольников;
-познавательныеУУД: формировать навыки синтеза и анализа информации, формирование логического мышления, работать с информацией.
Личностные УУД: формирование мотивации.
Оборудование: мультимедийный проектор, компьютер, экран, раздаточный материал, чертёжные инструменты.
План урока:
1. Организационный момент. Самоопределение к деятельности.
2. Актуализация опорных знаний. Целеполагание.
3. Самостоятельное открытие новых знаний экспериментальным путём в привычной и новой ситуациях.
4. Физкультминутка. (подвижная)
5. Первичное закрепление и применение новых знаний.
6. Первичная проверка понимания. Тест с последующей самопроверкой.
7. Подведение итогов. Домашнее задание.
8. Рефлексия.
Структура и ход урока
|
Этапы урока |
Деятельность учителя |
Деятельность учащихся |
|
1. Этап. Организационный момент. Самоопределение к деятельности.
Слайд 1
|
Приветствует детей. Проверяет готовность к уроку.
- Здравствуйте, ребята! Садитесь. Меня зовут Ольга Сергеевна – я учитель математики Брейтовской школы, находящейся на другой стороне Рыбинского водохранилища на расстоянии 290 км.от Ярославля и очень рада встрече с вами надеюсь на нашу с вами совместную плодотворную работу и вашу поддержку.
- Ребята, внимательно посмотрите на экран. (слайд 1) -- Как вы думаете, чему будет посвящён сегодня наш урок? - Какая геометрическая фигура называется треугольником? Перечислите элементы треугольника. Сегодня каждый из вас на уроке может сделать маленькое открытие. Для этого от вас требуется внимание, активность и желание работать. Успехов вам и удач!
( слайд 2)
|
К): слушают учителя (Л): эмоциональный настрой
Отвечают на поставленные вопросы: Треугольникам
Прямоугольный, тупоугольный, равносторонний, равнобедренный.
Дают определение равнобедренного треугольника, называют его элементы Дают определение прямоугольного треугольника Формулируют свойство углов равнобедренного треугольника Формулируют теорему о сумме углов треугольника. |
|
2. Этап. Актуализация опорных знаний. Целеполагание. Слайд 2
Слайд 3
Слайд 4
Слайд 5
Слайд 6
Слайд 7
|
- Какие треугольники вы видите на экране? - Какой треугольник называется равносторонним? тупоугольным? - Как вы думаете, можно ли построить тупоугольный равносторонний треугольник? - Чему равна сумма углов треугольника? - Какой треугольник называется равнобедренным? - Какими свойствами обладает равнобедренный треугольник? - Какой треугольник называется прямоугольным? - Как называются стороны прямоугольного треугольника? - Какая сторона называется гипотенузой треугольника? Задачи по готовым чертежам:
- Найдите угол треугольника? Что это за треугольник? Чем воспользовались для нахождения неизвестного угла?
- Чему равны углы в треугольнике? Что это за треугольник? Какое свойство вы применили для решения задачи?
- Можно ли свойство прямоугольного треугольника применить и к любому прямоугольному треугольнику?
- Что мы сегодня будем изучать на уроке? Сформулируйте тему нашего сегодняшнего урока.
- Запишите число и тему урока в тетради.
- Сформулируйте цель урока?
|
Прямоугольный, тупоугольный, равнобедренный, равносторонний
Дают определения каждого вида треугольников.
= 750. Теоремой о сумме углов треугольника.
= 500 и 500. Свойством равнобедренного треугольника.
Нет.
Формулируют тему урока, записывают себе в тетрадь. Свойства прямоугольных треугольников.
Записывают в тетрадь, число и тему урока.
Выяснить свойства прямоугольных треугольников, научиться применять их на практике. |
|
3. Этап. Самостоятельное открытие новых знаний экспериментальнымпутём в привычной и новой ситуациях.
Слайд 8
Слайд 9
Слайд 10
Слайд 11
Слайд 12
|
Ребята! Очень часто ученые устанавливают важные факты экспериментальным путем. Это происходит в разных областях науки: в физике, химии, математике. Я вам тоже сегодня предлагаю побыть в роли исследователей, провести эксперимент и открыть свойства прямоугольного треугольника.
- У каждой пары на столах лежат треугольники разного цвета. - Возьмите транспортир и измерьте острые углы этих треугольников, и вычислите сумму их градусных мер. Результаты запишите себе в лист с опорным конспектом. - Сделайте вывод.
А кто может объяснить почему?
- В этом и состоит одно из свойств прямоугольных треугольников.
- Проведём второй эксперимент: возьмите треугольники розового цвета, измерьте длины гипотенузы и катета, лежащего против угла в 300. - Запишите результаты себе на лист с опорным конспектом.
Сделайте вывод.
- А сейчас давайте посмотрим на наши треугольники. Легко заметить, что у каждого из вас в руках прямоугольный треугольник, но отличающийся от других.
Как вы думаете, случайно ли у все получился одинаковый результат? - Любую гипотезу нужно либо доказать, либо опровергнуть. Попробуем доказать?
(Катет прямоугольного треугольника, лежащий против угла в 300, равен половине гипотенузы.) - Докажем данное свойство.
-Приложите модели друг к другу, совместив катеты АВ (клетчатые) - Какая фигура получилась?
- Мы сегодня работаем с треугольников, поэтому перестройте свои модели, так, чтобы получился треугольник. - Какой треугольник получили? ( ДВС ) - Что мы знаем о нём? ( равносторонний) - Чем является АВ в этом треугольнике? (Высотой, медианой и биссектрисой) - Значит отрезок АС равен половине ВС.
Мы с вами доказали гипотезу, которая выражает второе свойство прямоугольного треугольника.
Свойства прямоугольного треугольника мы доказали экспериментально, но есть и научное подтверждение, где мы их можем посмотреть? - Работа с учебником стр. |
Измеряют градусные меры углов, находят сумму, записывают вывод в тетрадь. Сумма острых углов прямоугольного треугольника равна 900.
По теореме о сумме углов треугольника: ………….
Измеряют длины катета, лежащего против угла в 300 и длину гипотенузы
Делают вывод, о том, что катет лежащий против угла в 300 равен половине гипотенузы.
(опорный конспект, заполняют пропуски)
Нет.
Да.
Работают с моделями, исследуют ситуацию, высказывают предложения, делают выводы.
(параллелограмм или треугольник)
Мы с вами выдвинули гипотезы и экспериментальным путём их доказали, а как называется такое утверждение в учебнике? (теоремой)
- в учебнике |
|
4. Этап. Физкультминутка (подвижная)
|
Организует физкультминутку. Просит учащихся изобразить углы: смежные, вертикальные, прямой, развёрнутый; параллельные прямые, пересекающиеся прямые, треугольник. |
Выполняют задания учителя. |
|
5.Этап. Первичное закрепление и применение новых знаний
Слайд 13
Слайд 14
Слайд 15
Слайд 16
Слайд 17
Слайд 18
Слайд 19
|
Повторим, какие свойства прямоугольного треугольника мы открыли. - А как вы думаете, для чего изучаются свойства? Решение задач № 254 (учебник) 1 ученик у доски.
Задача №254. Дано: ΔАВС – прямоугольный, равнобедренный, ÐВ= 90º
Найти: ÐA, ÐC
Решение: т.к. ΔАВС –равнобедренный, то АВ=ВС, ÐA =ÐC (по свойству равнобедренного треугольника) ÐA +ÐC= 90º (по 1 свойству прямоугольных треугольников) Пусть ÐA =ÐC= х, тогда х+х=90 х=450 ÐA =ÐC=450 Ответ:450,450.
- Ребята, а где в жизни вам встречались прямоугольные треугольники? - Я вам подготовила несколько задач, в которых данные треугольники встречаются в нашей жизни.
По данным рисунка решите задачу.
Катет = 150
Гипотенуза равна 12
Свойство о сумме острых углов прямоугольного треугольника нашло широкое применение в транспортной, космической технике. - Это свойство лежит в основе конструкций простейшего уголкового отражателя. Так, уголковый отражатель, или КАТАФОТ, устанавливается на заднем крыле велосипеда для того чтобы «возвращать» свет автомобильных фар. Это даёт возможность водителю автомобиля видеть в тёмное время суток едущий впереди велосипед. Прежде чем садиться за руль велосипеда, необходимо установить уголковый отражатель в целях безопасности движения.
Прямоугольные треугольники, также широко применяются в оригами. Оригами – складывание фигурок из бумаги. (приводит пример)
|
Формулируют свойства
Для облегчения вычислительной работы.
Решение данной задачи проводит один учащийся у доски, остальные записывают решение в тетради.
Решают задачи по готовым чертежам.
(Л): удовлетворять потребность в самовыражении (К): воспринимать ответы обучающихся, участвовать в диалоге (Р): осуществлять самоконтроль и самооценку своих действий, участвуя в оценке действий других. Принимать и сохранять учебную цель и задачу.
Слушают учителя, если есть необходимость задают вопросы. |
|
6. Этап. Первичная проверка понимания. Тест с после-дующейвзаимопроверкой. Слайд 20
|
Тестовая работа
|
Выполняют тест самостоятельно, осуществляют взаимопроверку (Р): Осуществлять самоконтроль, оценивать качество и уровень усвоения знаний |
|
7.Этап. Подведение итогов урока. Домашнее задание.
Слайд 21
|
- Какие свойства прямоугольных треугольников мы узнали? - Что мы использовали для достижения цели урока? - Достигли ли мы поставленной цели? - Ребята, а как вы думаете у прямоугольного треугольника только два свойства? - Свойства прямоугольного треугольника необходимы для решения задач выпускного экзамена в 9 классе. Я вам хочу предложить как домашнее задание решить несколько экзаменационных заданий по выбору. ( п. 35) |
сегодня на уроке я повторил…… я узнал…….., я научился……., было интересно…., было трудно…., я понял что… (К): осознание себя в коллективе, значимости совместной работы, реф-лексия своих действий, оценивание работы на уроке(П): выделение и осознание учащимися того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения (Л): самооценивание |
|
8. Этап. Рефлексия.Слайд 22
Слайд 23 |
Оцените свою работу на уроке:Перед каждым из вас лежат прямоугольные треугольники разного цвета. Соберите из них волшебный цветок -зеленого цвета, если вы активно работали и считаете, что усвоили новый материал -желтого цвета: если вы недостаточно хорошо поняли новый материал; -красного цвета: если вы ничего не поняли из новой темы. -Вы замечательно сегодня поработали, мне очень приятно. Надеюсь, этот материал вы не забудете, и он поможет вам в изучении следующих тем геометрии. Спасибо за урок! |
Оценивают свою работу на уроке, собирают волшебный цветов технике оригами. |
ПРИЛОЖЕНИЕ 4
Конспект урока по теме Площадь треугольника» геометрия 8 класс
Технологическая карта урока
Наглядность – «золотое правило дидактики»
Я.А.Коменский.
Тема учебного раздела: Площадь
Место урока в теме: 1 урок по теме «Площадь треугольника»
Продолжительность: 40 минут.
Предмет, класс, в котором используется продукт: геометрия, 8 класс.
Авторы учебника, учебно-методического комплекта:Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. Геометрия 7-9 класс (ФГОС)
Тип урока: урок изучения нового материала и первичного закрепления знаний по теме «Площадь треугольника».
Оборудование и средства обучения: компьютер, мультимедийный проектор, раздаточный материал, набор чертёжных инструментов, карточки для самостоятельной работы
Формы организации труда: индивидуальная, фронтальная, работа в парах, самостоятельная.
Педагогические технологии: системно - деятельностный подход (технология проблемно-диалогического обучения)
Методы обучения: словесный, наглядный, практический, репродуктивный, частично-поисковый.
Пояснительная записка: при подготовке урока в 8 классе я руководствовалась возрастными особенностями учащихся и государственным стандартом по математике (геометрии).
Основные понятия урока:Прямоугольный треугольник, произвольный треугольник, площадь треугольника, параллелограмма, прямоугольника, катеты треугольника, высота и основание треугольника, параллелограмма. Понятие площади и её свойства, равновеликие фигуры.
Дидактическая цель урока: создать условия для вывода формул площади прямоугольного и произвольного треугольников, и их применения в процессе решения задач.
Задачи урока:
Образовательные:
· способствовать формированию понятий «площади треугольника»;
· сформировать навыки применения формул при решении практической и исследовательской работ.
Развивающие:
· продолжить формирование умения устанавливать причинно-следственные связи, работая в паре;
· формирование умений сравнивать, обобщать факты и понятия;
· способствовать развитию познавательного интереса к изучаемому предмету;
· способствовать развитию воображения, творческой активности учащихся, мышления, внимания
Воспитательные:
· способствовать воспитанию чувства само- и взаимоуважения, чувства товарищества;
· способствовать развитию сотрудничества при работе в парах;
· воспитывать уверенности в себе, мотивацию к обучению
Здоровье сберегающий аспект урока:
- доброжелательная атмосфера, способствующая положительному эмоциональному настрою;
- создание ситуации успеха на уроке;
- чёткая организация урока;
- физкультминутка для снятия усталости.
План урока.
11. Организационный момент. (проверка готовности к уроку) ( 1 мин)
12. Актуализация опорных знаний учащихся. Решение задач на готовых чертежах с целью закрепления формулы для площади параллелограмма. (6 мин)
13. Целеполагание. Мотивация. Постановка проблемной ситуации (3 мин)
14. Изучение нового материала. Практическая работа . (7 мин.)
Решение проблемной ситуации
15. Первичное закрепление нового материала Решение задач (5 мин)
16. Физкультминутка. (1 мин)
17. Закрепление и применение изученного. Работа с учебником (решение заданий). ( 6 мин)
18. Применение знаний в новой ситуации.формулы на итоговой аттестации учащихся. (7 мин)
19. Итогово - оценочный. Домашнее задание. (3 мин)
20. Рефлексия.(1 мин)
ХАРАКТЕРИСТИКА УРОКА
|
Техноло-гии, приме-няемые на уроке |
Решаемые проблемы |
Виды деятельности (элементы содержания, контроль) |
Планируемые результаты |
||
|
предметные |
УУД |
личностные |
|||
|
Проблем-ного обучения, информационно-коммуни-кативныетехноло-гии
|
По какой формуле можно вычислить площадь треугольника? Как найти площадь прямоугольноготреугольника? |
устная работа, работа в паре, работа с текстом учебника, работа у доски, фронтальная работа с классом. |
ПРЕДМЕТНЫЕ ученик научится находить площадь треугольника; ученик получит возможность применять полученные знания при решении задач с практическим содержанием. МЕТАПРЕДМЕТНЫЕ ученик научится определять понятия, создавать обобщения, устанавливать аналогии с известными правилами; ученик получит возможность научиться элементам волевой саморегуляции, мобилизации сил к преодолению препятствий.
|
Коммуникативные: уметь точно и грамотно выражать свои мысли; уметь слушать других, умение находить общее решение, аргументировать свою точку зрения
Регулятивные:работать по составленному плану, формировать целевые установки учебной деятельности, выстраивать алгоритм действий; умение адекватно оценивать правильность или ошибочность выполнения учебной задачи.
Познавательные: осуществлять поиск необходимой информации для выполнения учебных заданий, умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение.
|
Формирование познавательного интереса к изучению нового; проявление способности к эмоциональному восприятию математических объектов, задач, решений, рассуждений ученик получит возможность контролировать процесс и результат учебной и математической деятельности |
Технологическая карта урока
|
Содержание учебного материала. Деятельность учителя
|
Деятельность обучающихся |
ФОУД |
Формирование УУД |
|
1-й этап. Организационный момент. Цель этапа: настроить учащихся к учебной деятельности. |
|||
|
· Приветствие · Проверка готовности учащихся к уроку · Настрой учащихся на работу. (Слайд 3) |
Активное слушание, взаимодействие с учителем. |
Ф |
П. Формулирование собственных ожиданий. Р. Проявление эмоционального отношения в учебно-познавательной деятельности. К: планирование учебного сотрудничества с учителем и одноклассниками |
|
2-й этап. Актуализация знаний. Цель этапа: актуализировать мыслительные операции. |
|||
|
Организует
устную фронтальную работу, демонстрирует задания с использованием слайдовой
презентации. (Слайд
4 - 6.) Предлагает повторить определение площади, свойства площадей фигур; формулы площадей изученных многоугольников (Слайды 7-10)
|
Взаимодействуют с учителем во время опроса, участвуют в принятии решений. Решают задачи по готовым чертежам.
Все включаются в работу.
Устно решают предложенные задания на нахождение площади фигур.
Объясняют, почему воспользовались той или иной формулой для нахождения площади
|
Ф
И |
П. Учатся извлекать информацию из иллюстраций, анализ объектов с целью применения к ним формул. К. Учатся слушать, вести диалог в соответствии целями и задачами общения. Р. Умение слушать в соответствии с целевой установкой, дополнять, уточнять высказанные мнения. Выбирают действия в соответствии с поставленной задачей. Л. Осуществляют актуализацию личного жизненного опыта. |
|
3-й этап. Целеполагание и мотивация. Создание проблемной ситуации. |
|||
|
Обеспечивает мотивацию учения школьников и принятие ими целей урока: предлагает решить жизненную задачу на нахождение площади четырёхскатной крыши беседки, имеющую форму треугольника (слайд 11).
Просит учащихся сформулировать тему и цели урока (слайды 12,13)
Постановка проблемы: как найти площадь треугольника? |
Оценивают недостаточность знаний для нахождения площади треугольника. Формулируют тему, ставят цель урока.
Выявляют место затруднения. Проговаривают причину.
|
Ф
|
П. Самостоятельно выделять и формулировать познавательную цель ; умение формулировать проблему. Л. Готовность и способность обучающихся к саморазвитию К. Формулировать и высказывать собственное мнение, умение определять общую цель и пути её достижения. Р. Ставить новые учебные задачи в сотрудничестве с учителем; осуществление целеполагания. |
|
4-й этап. Изучение нового материала. Практическая работа. Решение проблемной ситуации. Цель этапа: вывести (получить) формулу для вычисления площади треугольников(прямоугольного и произвольного). |
|||
|
1. Организует исследование (практическую работу). Подводит к выводу формулы прямоугольного и произвольного треугольников с помощью наводящие вопросов. Помогает учащимся в решении поставленной проблемы.
2.Организует вывод формулы площади прямоугольного треугольника и формулы площади произвольного треугольника
|
Выполняя задания в соответствии с этим планом, ученики все промежуточные действия и конечные выводы записывают в тетради.
Взаимодействуют с учителем, отвечают на его вопросы в ходе выполнения практической работы; записывают в тетради информацию по ходу выполнения данной работы
Все включаются вработу. |
ФИ |
П. Самостоятельное выделение и формулирование познавательной цели, поиск и выделение необходимой информации, осознанное построение речевого высказывания в устной и письменной форме. Анализ и синтез информации.Самостоятельное создание способов решения проблем поискового характера. К.Планирование учебного сотрудничества с учителем и сверстниками, умение полно и точно выражать свои мысли. Р. Постановка учебной задачи на основе соотнесения того, что уже известно и усвоено, и того, что ещё неизвестно. Прогнозирование, контроль, коррекция, саморегуляция. Л. Постепенное накопление учащимися информации (от простого к сложному), установление связи между целью учебной деятельности и её мотивом. |
|
5-й этап. Первичная проверка и понимание изученного. Цель этапа: рассмотреть применение формулы для вычисления площади треугольника на решении устных заданий. |
|||
|
Давайте закрепим полученную информацию на практике. Обращает внимание на нахождение площади прямоугольного треугольника. Устно выполнить следующие задания: а) по учебнику № 468 (а, б ), 471.
б) предлагает устные задания с макетами треугольников на доске (приложение) |
Ответы учащихся (устная работа по нахождению площадей треугольников)
Работа с учебником.
|
Ф |
П. Выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. К.Планирование учебного сотрудничества с учителем и сверстниками, умение полно и точно выражать свои мысли. Р. Прогнозирование, контроль, коррекция, саморегуляция. |
|
6-й этап. Физкультминутка. Цель этапа: предупреждение утомляемости учащихся. |
|||
|
Проводит
физкультминутку. |
Выполняют гимнастику. |
|
|
|
7-й этап. Закрепления и применения изученного. Цель этапа: при решении задач отработатьприменение формулы для вычисления площади треугольника |
|||
|
Организует решение упражнений из учебника:
( можно рассмотреть № 472) |
Один решает у доски с комментированием, остальные в тетрадях.
Индивидуальное решение с последующей проверкой.
|
Ф
И |
П. Выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Осознанное построение речевого высказывания в устной и письменной форме; построение логической цепочки рассуждений. К. Умение с достаточной полнотой и точностью выражать свои мысли. Р. Прогнозирование, контроль, коррекция, саморегуляция. Л. Личностное самоопределение, установление обучающимися связи между целью учебной деятельности и её мотивом (смыслообразование), оценивание усваиваемого содержания. |
|
8-й этап. Применение знаний в новой ситуации . Цель этапа: умение применить знания в новой ситуации. |
|||
|
Учащимся предлагаются задания из вариантов ОГЭ для работы в парах. Учитель демонстрирует слайды презентации, координирует работу обучающихся, консультирует их.
Решение задач на клетчатой бумаге. |
Выстраивают систему аргументов для убеждения, продумывают ответы и обсуждают их с соседом по парте. Сравнивают свое решение с образцом, находят и исправляют ошибки.
|
П
И |
П. Развитие и углубление потребностей и мотивов учебно-познавательной деятельности. К. Взаимодействуют с соседом по парте, учитывают позицию собеседника, осуществляют сотрудничество и кооперацию с учителем и одноклассником. Р. Оценивают предложенные варианты, выбирают наиболее точный. Происходит восприятие, осмысление, запоминания материала. |
|
9-й этап. Итогово - оценочный. Цель этапа: организовать целостное осмысление и обобщение полученной информации, проведение самооценки учениками работы на уроке. |
|||
|
1. Мотивирует обучающихся к самоанализу деятельности и проектированию дальнейшего продвижения в изучении темы. Организует обсуждение достижений, ставя заранее подготовленные вопросы.
2.
Подводит итоги урока. 3. Формулирует домашнее задание. Даёт пояснения по его выполнению.
|
Участвуют в беседе по обсуждению достижений, отвечая на вопросы учителя, делают выводы. Оценивает каждый сам себя.
Записывают домашнее задание в дневник |
Ф |
П. Самостоятельное выделение и формулирование познавательной цели, поиск и выделение необходимой информации. К. Умение с достаточной полнотой и точностью выражать свои мысли. Разрешение конфликтов. Р.Прогнозирование, волеваясаморегуляция. Л. Личностное самоопределение, смыслообразование. |
|
10-й этап. Рефлексия учебной деятельности. |
|||
|
Организует рефлексию и самооценку учениками собственной учебной деятельности. Продолжите фразы: «Сегодня на уроке я узнал…» «Мне было труднее всего…» «Самым полезным для меня было…» «Я понял, что…» «Я научился…» «Мне захотелось…» «Знания, полученные на уроке, мне пригодятся…» |
Отвечают на вопросы учителя.
Выполняют самооценку
|
Ф |
П. Поиск и выделение необходимой информации, построение речевого высказывания в устной форме. Анализ и синтез информации. К. Умение полно и точно выражать свои мысли; учёт разных мнений. Р. Самооценка на основе критерия успешности Л. Адекватное понимание причин успеха (неуспеха) в учебной деятельности. |
Примечание к таблице: ФОУД – форма организации учебной деятельности обучающихся (Ф – фронтальная, И – индивидуальная, П – парная, Г – групповая)Сокращения, используемые в столбце формируемые УУД (универсальные учебные действия): П – познавательные, Л-личностные, К-коммуникативные, Р – регулятивные.
Скачано с www.znanio.ru
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.