Методическая разработка урока по математике Уравнения и неравенства с модулем"

Пояснительная записка

Зарождение математики произошло от потребностей человека решать проблемы быта и существования, постепенно математика стала развиваться как самостоятельная наука. 

Решение уравнений и неравенств имеет особое место и в 21 веке. 
Уравнения и неравенства  могли решать еще в глубокой древности, чтобы решить уравнение учёным приходилось делать большие вычисления. Неравенствами  занимались такие известные математики как Эйлер, Виет, Ньютон, Гаусс. 
      В повседневной жизни, экономике, сельском хозяйстве, металлургии и т.д. нам приходится решать задачи с помощью уравнений и неравенств. 
Уравнения и неравенства  расширяют умственный кругозор, повышают интерес к математике, углубляется понимание изучаемого, повышают   культура и осознание роли математики в современном обществе. 
     В структуре изучаемой дисциплины «Алгебра и начала математического анализа; геометрия» выделяется следующий  раздел: «Уравнения и неравенства». Содержание раздела «Уравнения и неравенства» включает тему урока «Уравнение и неравенства с модулями » .

В результате изучения данной темы студент должен

Знать:

-определение уравнения, неравенства, модуля;

-виды уравнений и неравенств;

-свойства модуля;

-способы решения  уравнений и неравенств с модулями;

Уметь:

-определять основные свойства модуля при решении уравнений и неравенств;

-применять способы решения уравнений и неравенств с модулями;

Тема урока : Уравнение и неравенства с модулями

Образовательная цель: 

-закрепление навыков решения уравнений и неравенств, содержащих модуль, традиционными способами;

-формирование навыков решения их, используя свойства модуля;

Развивающая цель: 

-развитие продуктивного мышления и навыков самоконтроля в  процессе выполнения упражнений;

-развитие умений логически мыслить и аргументировано отстаивать  свои убеждения.

Воспитательная цель: 

-воспитывать информационную культуру и культуру общения, готовить обучающихся к            

жизни в современном информационном обществе

Тип урока: урок обобщения и систематизации знаний

Вид урока:  практическая работа

Методические приемы:

-самостоятельная работа (тест);

-практический- решение математических задач.

Оборудование и наглядные средства обучения: компьютерный класс с ОС Windows 8 и пакетом программ Microsoft Office 2010 (10 ПК), мультимедийный проектор, интерактивная доска SmartBoard, программа Notebook, колонки, демонстрационный и раздаточный материал, презентация  в Notebook, в Power Point.

Методическая цель: способы активизации мыслительной деятельности студентов

Ход урока:

I.Организационный момент: Подготовка учащихся к уроку                          

(проверка отсутствующих на уроке, наличие тетрадей)

– Сегодня на уроке мы повторим и закрепим умения решать уравнения и неравенства с модулем, а также узнаем о некоторых утверждениях, применение которых позволит упростить решение некоторых из них. 

II. Актуализация опорных знаний

1.Решите пример устно и выберите правильный ответ

1. Какому промежутку принадлежит сумма корней уравнения ?

1) (10;+)
2) [ 10 ; 30 ]
3) ( –– 10 )
4) [ – 10; 10 ).

Ответ: 2.

2. Найти сумму целых решений неравенства .

1) 20
2) –12
3) 12 5) –20.

Ответ: –20.

3. На каком рисунке изображен график функции у = ?

Ответ: третий рисунок.

2.Дайте определение понятие модуль.

«Модуль» (от лат. modulus-мера)  ввёл английский математик Р. Котес  (1682–1716). Знак модуля – немецкий математик (в 1841г.) К. Вейерштрасс (1815–1897).

Модуль числа a  есть расстояние от нуля до точки a, 

Модуль разности двух чисел равен расстоянию между точками числовой прямой, соответствующим этим точкам.

Используя определение модуля и его  геометрический смысл, можно решить простейшие уравнения и неравенства с модулем. Простейшие уравнения и неравенства удобно решать с помощью равносильных преобразований:  возведение в квадрат и т.д.

3.По таблице расскажите о классификации уравнений и неравенств с модулем.

ΙΙΙ. Практическая часть.

1.Решите уравнение:

1. (x - 2)² - 8│x -2│+ 15 = 0

Решение.  │x -2│= t, t >0

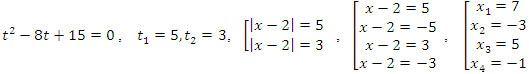
Ответ {-3; -1; 5; 7}

2. x² + │x │- 6 = 0 (учащиеся решают самостоятельно).

Решение.  │x │= t, t >0

t² + t - 6 = 0, t₁ = -3, t₂ = 2, │x │= 2, x₁ = -2, x₂ = 2

Ответ  x₁ = -2, x₂ = 2

3. x² -│x │- 12 ≥ 0

Решение.  │x │= t, t >0

4.

 + 

Решение

1. 
2. 
3. 

,; ;  ; ; .

2. 

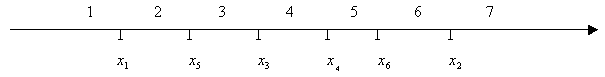
Легко заметить, что на первом и седьмом, втором и шестом, третьем и пятом промежутках модули имеют равные знаки.

1. x , x, +2–3 = 0, –3 = –3 

2. , –+2–3 = 0 , 2+10+12 = 0  Первый корень является решением, второй – нет.

3. ;1);. –+2 . Первый корень не является решением, второй – является.

4. 

Ответ: .

Объяснение учителя.

– Большой пример? А еще больше его решение. Посмотрите внимательно “ пристальным взглядом”. Что заметили? (что сумма выражений, стоящих слева, равна выражению, стоящему справа)

Если или, т.е. .

Докажем, что это равенство верно, если .

Доказательство: , так как – верно, если .

– На дополнительном материале к уроку ( на столе у учащихся) написаны утверждения, которые облегчат решение некоторых уравнений и неравенств, содержащих модуль. Перепишите их в тетрадь и попробуйте, если возможно, применять их при решении примеров.

1. .

2.,

3. 

4. 

5. 

6.  решений нет.

7. .

8. .

9. 

2.Решите неравенство:

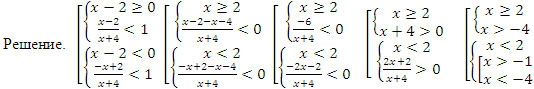
Ответ (-∞;-4] U [-1; +∞)

2)  (учащиеся решают самостоятельно, проверка по слайду).

ΙV. Закрепление пройденного материала.

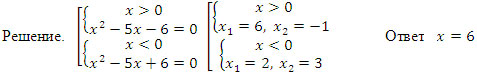
1.Самостоятельная работа (по вариантам)

Вариант №1.

1. │-x² + x - 1│= │-x² + 2x + 3│,

Ответ {-4; 2; -0,5}

2. (x - 2)² - 8│x -2│+ 15 = 0

Решение.  │x -2│= t, t >0

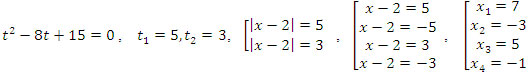
Ответ {-3; -1; 5; 7}

Вариант №2. 

1.│x + x² - 3│≤ │x - 2 + 2x²│

Решение. (x + x² - 3 + x - 2 + 2x²)(x + x² - 3 - x + 2 - 2x²) ≤ 0

(2x + 3x² - 5)(-x² - 1) ≤ 0, (2x + 3x² - 5)(x² + 1) ≥ 0, (2x + 3x² - 5) ≥ 0

2. Пример №2. x² + │x │- 6 = 0 (учащиеся решают самостоятельно).

Решение.  │x │= t, t >0

t² + t - 6 = 0, t₁ = -3, t₂ = 2, │x │= 2, x₁ = -2, x₂ = 2

Ответ  x₁ = -2, x₂ = 2

Вариант №3.

1.│3x - 1│< │2x - 5│ (учащиеся решают самостоятельно).

(3x - 1 + 2x - 5) (3x - 1 - 2x + 5) < 0, (5x - 6)(x + 4) < 0, -4 < x < 1,2

Ответ (-4; 1,2)

2.. x² -│x │- 12 ≥ 0

Решение.  │x │= t, t >0

Вариант № 4.

1.2│x - 1│- 3│x + 4│= 1

Решение. x₁ = 1, x₂ = -4

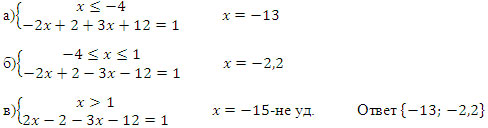
2.│ x² - 2x│+ │x - 1│≤ x²

Решение. │ (x - 2)x│+ │x - 1│≤ x²

x₁ = 0, x₂ = 2, x₃ = 1

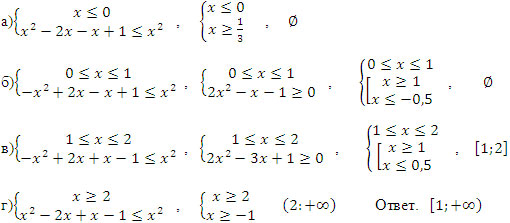
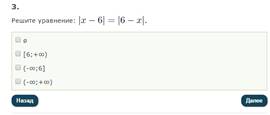
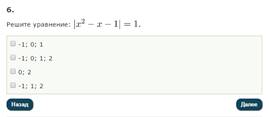
2.ТЕСТ.( http://egemaximum.ru/test-po-teme-modul-prostejshie-uravneniya-s-modulem/)

V. Итоги урока: выставление оценок

Домашняя работа

Решите уравнения методом

Замена переменной.

1) (x - 2)2 - 8│x - 2│+ 15 = 0,

2) x2 + │x│- 6 = 0,

3) x2 - 2x - 5│x - 1│+ 5 = 0.

4) x2 - │x│- 12 ≥ 0,

5) 20 - 3x2 + 11│x │> 0,

6) x2 - 2x + 1 < 2│x - 1│.

Интернет-ресурсы:

www.ziimag.narod.ru - персональный сайт автора Мордковича А. Г. "Практика развивающего обучения".

www.math.ru -Интернет - поддержка учителей математики.

www.it-n.ru-Сеть творческих учителей. Материалы и ресурсы, касающиеся использования ИКТ в учебном процессе:

– библиотека готовых учебных проектов с применением ИКТ, а также различные проектные идеи, на основе которых можно разработать свой собственный проект;

– библиотека методик проведения уроков использованием разнообразных электронных

ресурсов;

– руководства и полезные советы по использованию программного обеспечения в учебном процессе;

– подборка ссылок на интересные аналитические и тематические статьи для педагогов.

www.exponenta.ru -Образовательный математический сайт. Содержит материалы по работе с математическими пакетами Mathcad, MATLAB, Mathematica, Maple и др. Методические разработки, примеры решения задач, выполненные с использованием математических пакетов. Форум и консультации для студентов и школьников.

http:school-collection.edu -Единая коллекция цифровых образовательных ресурсов. Цифровые образовательные ресурсы (ЦОР) к учебникам.

http://www.intellectcentre.ru – сайт издательства «Интеллект-Центр», -тренировочные материалы, демонстрационные версии, банк  тренировочных заданий с ответами, методические рекомендации и образцы решений.

Скачано с www.znanio.ru