
Методическая разработка занятия
«Метод перекрывающихся площадей»
Учитель математики: Руднева Наталья Николаевна
Тема: Метод перекрывающихся площадей
Тип урока: Урок изучения нового материала Формируемые результаты занятия:
Предметные: формировать умение применять метод перекрывающихся площадей при решении задач.
Личностные: формировать умение планировать свои действия в соответствии с учебным заданием.
Метапредметные: формировать умение устанавливать причинно- следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и делать выводы.
Планируемые результаты: Учащийся научится применять метод перекрывающихся площадей при решении задач.
Основные понятия: Площадь треугольника, площадь четырехугольника, свойства площадей, метод площадей, перекрывающиеся площади.
Описание хода урока
I. Организационный момент. (2 мин)
Приветствие. Проверка готовности класса к занятию. Использование педагогических приёмов наведения дисциплины в классе.
II. Постановка цели и задач урока. Формулирование темы урока.
Форма организации учебной деятельности: фронтальная
Слайд 1
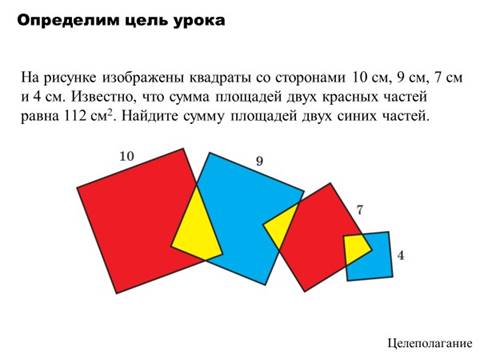
Вопросы для построения диалога:
Каково взаимное расположение квадратов на рисунке? [квадраты наложены друг на друга]
Что можете сказать про площади желтых частей? [площади желтых частей являются общей частью площади двух квадратов – синего и красного]
Как бы вы назвали площади желтых фигур? [перекрывающиеся]
Что требуется найти? [площадь синих квадратов]
Как можно назвать метод решения данной задачи, исходя из специфичного расположения фигур? [Метод перекрывающихся площадей] Сформулируйте тему занятия. [Метод перекрывающихся площадей]
Сформулируйте цель занятия. [Применение метода перекрывающихся площадей при решении задач]
Что мы должны сделать чтобы достичь данной цели? Сформулируйте задачи занятия.
[Задачи занятия:
1. Сформулировать и усвоить суть метода перекрывающихся площадей.
2. Научиться, используя свойства площадей, выражать площади перекрывающихся фигур.
3. Научиться решать задачи с помощью метода перекрывающихся площадей.]
III. Актуализация опорных знаний (Вхождение в тему урока и создание условий для осознанного восприятия нового материала)
Форма организации учебной деятельности: фронтальная
Приём: Решение задач на готовых чертежах
Слайд 2
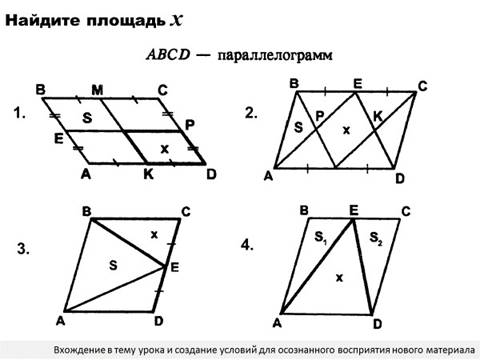
Вопросы (к слайду 2) для построения диалога:
1. Какие свойства площадей вы использовали для нахождения площади x?
2. Какое дополнительное построение необходимо сделать для параллелограмма, чтобы установить зависимость площади параллелограмма и треугольников? 3. Найдите равновеликие и равносоставленные фигуры в каждой комбинации 1-4.
Слайд 3
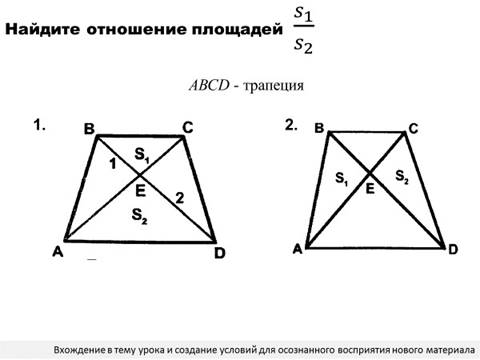
IV. Мотивация учебной деятельности
Форма организации учебной деятельности: индивидуальная
Приём: «Мотивационные вопросы»
✓ Как я планирую организовать свою работу на занятии?
✓ При каких условиях занятие будет для меня полезным?
✓ Где я буду применять знания и умения, получаемые на данном занятии?
V. Решение заданий (Организация и самоорганизация учащихся. Организация обратной связи) Форма организации учебной деятельности: фронтальная, парная
|
Ресурсный материал по содержанию урока
|
Этапы организации деятельности учащихся при решении задач |
Результат деятельности учащихся (по этапам) |
Помощь учителя |
|
1. Дано: ABCD—параллелограмм; E∈BC, F∈AD; AE∩BF=M, ED∩FC=N.
Доказать: а) SAMF +SFND = SBME +SENC; б) SMENF =SABM +SNCD. |
1) Постановка учебной цели в процессе решения задачи; 2) выявление средств, необходимых для решения задачи;
3) соотнесение выявленных средств выполнения учебно- познавательной деятельности (далее -УПД) с собственными знаниями и умениями, принятие решения о помощи, выбор уровня самостоятельности; 4) поиск решения задачи;
|
1) Найти и обобщить способ решения данной задачи;
2) Перечисляют: а) свойства площадей; б) формулы для вычисления площадей; в) приём работы с задачей: выведение следствий из условия и требования. 3) Формулируют свойства площадей; записывают формулы для вычисления площади параллелограмма, треугольника.
4) Работа с текстом задачи: анализируют условие и чертеж; изображают фигуру в соответствии с условием задачи, записывают данные и требование: «Дано», «Доказать». Поиск решения задачи: Выводят следствия из условия задачи: Точки E∈BC, F∈AD, причем BC ‖ AD, то можно использовать свойство площадей треугольников в параллелограмме. Выводят следствия из требования: для доказательства а) нужно на чертеже найти фигуру, которая была бы составлена из данных |
Помогает назвать нужные теоретические факты и этапы решения задачи.
Предлагает: ✓ Постараться вспомнить, что ещё известно про площади фигур; ✓ Придумать, какие фигуры должны получиться при разбиении и пересекающихся площадях. |
|
|
5) составление решения задачи;
6) реализация плана;
|
плана
|
треугольников – такие фигуры есть - 𝛥𝐵𝐹𝐶 и 𝛥𝐴𝐸𝐷. Если поиск решения задачи не закончен – то выбирают способ помощи и уровень помощи. 1 уровень: воспользоваться идеей метода решения: перекрывающиеся площади. 2 уровень: воспользоваться перечнем обоснований, необходимых для решения задачи; 3 уровень: по готовой схеме поиска решения задачи вспомнить формулировки теорем – обоснований и разобрать решение задачи. 5) Составляют план решения: А) 1. Доказать SBFC = SAED 2. Используя свойство площадей, записать чему равны площади треугольников 𝛥𝐵𝐹𝐶 и 𝛥𝐴𝐸𝐷. 3. Выделить пересекающиеся площади в 𝛥𝐵𝐹𝐶 и 𝛥𝐴𝐸𝐷. 4. Используя свойство аддитивности, доказать требуемое утверждение. Б) 1. Дополнительное построение: провести высоту к основанию АD. 2. Доказать, что SABF +SFCD= 0,5 SABCD. 3. Доказать, что SABF +SFCD = SBFC. 4. Используя свойство аддитивности, площадей доказать требуемое утверждение. 6) Записывают решение задачи. Обобщают решение задачи. Фиксируют в устной речи созданный приём: 1. Найти равновеликие фигуры с пересекающимися площадями или сделать дополнительное построение, чтобы их найти; 2. Выяснить, из каких частей состоят искомые фигуры; |
Даёт образец решения для контроля. Помогает правильно сформулировать отдельные шаги приёма.
|
|
|
7) контроль решения задачи;
8) Оценка процесса и результатов выполненной деятельности, с использованием соответствующих приёмов; 9) Коррекция собственной УПД
|
3. Найти (доказать равенство) площади фигур, входящих в искомую фигуру; 4. Используя свойство аддитивности площадей, выразить площадь искомой фигуры через известные площади фигур.
7) перечисляют все определения, свойства и теоремы, которые использовались при решении задачи.
8) Оценивают свою деятельность при решении задачи по пяти бальной системе.
9) Фиксирует свое внимание на ошибке и устанавливает её характер, анализирует причины ошибки – применение теоретических положений (определения, теоремы, формулы), делает вывод о причине ошибки, использует откорректированные знания и действия в процессе решения аналогичных задач. |
Предлагает перечислить умения, которые использовались. Предлагает зафиксировать оценку на листке контроля.
Предлагает коррекцию собственных учебных действий выполнить дома. |
|
2. Точки Е, F, К, L - середины сторон четырехугольника АВСD. Докажите, что сумма площадей треугольников АLМ, ВNЕ, СРF, КQD равна площади четырехугольника МNРQ. |
1) Применение приёма (метода) решения задачи 1 к решению данной задачи; 2) Перечисляют: а) свойства площадей; б) формулы для вычисления площадей; в) приём работы с задачей: выведение следствий из условия и требования. 3) Формулируют свойства площадей; записывают формулы для вычисления площади параллелограмма, треугольника. 4) Работа с текстом задачи: анализируют условие и чертеж; изображают фигуру в соответствии с условием задачи, записывают данные и требование: «Дано», «Доказать». |
Помогает назвать нужные теоретические факты и этапы решения задачи.
Предлагает: ✓ Постараться вспомнить, что ещё известно |
|
|
|
Осуществляют поиск решения задачи (выводит следствия из условия и следствия из требования; выясняет какие дополнительные построения можно выполнить, чтобы получить равновеликие фигуры с перекрывающимися площадями).
5) Составляют план решения. 6) Записывают решение задачи.
7) перечисляют все определения, свойства и теоремы, которые использовались при решении задачи.
8) Оценивают свою деятельность при решении задачи по пяти бальной системе.
9) Фиксирует свое внимание на ошибке и устанавливает её характер, анализирует причины ошибки – применение теоретических положений (определения, теоремы, формулы), делает вывод о причине ошибки, использует откорректированные знания и действия в процессе решения аналогичных задач.
|
про площади фигур; ✓ Придумать, какие фигуры должны получиться при разбиении и пересекающихся площадях.
Даёт образец решения для контроля. Предлагает другой способ решения. Предлагает перечислить умения, которые использовались. Предлагает зафиксировать оценку на листке контроля.
Предлагает коррекцию собственных учебных действий выполнить дома. |
VI. Проверка полученных результатов. Коррекция
Форма организации учебной деятельности: индивидуальная
Решение самостоятельно заданий по вариантам (№ 1 – I вариант, № 2 – II вариант) и последующей проверкой решения по эталону.
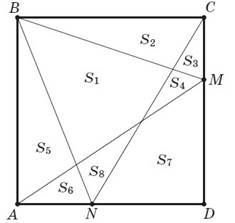
1. Дано: ABCD — квадрат; N∈AD, M∈CD; отрезки BN, CN, BM, AM делят квадрат на части с площадями S1 — S8.
Сравнить: площади S1 и S3 +S6 +S7.
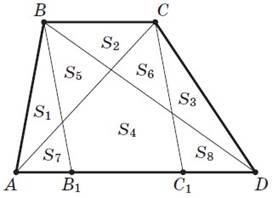
2. Дано: ABCD—трапеция (BC ‖ AD); BB1 ‖CC1, B1, C1 ∈ AD; отрезки AC, BD, BB1,
CC1 делят трапецию на части с площадями S1—S8. Доказать: S4 =S1 +S2 +S3.
VII. Подведение итогов урока. Рефлексия
✓ Какой метод решения планиметрических задач вы использовали сегодня на занятии?
✓ Какие пробелы в своих знаниях я заметил на уроке?
✓ Можно ли сказать, что я научился применять метод перекрывающихся площадей при решении задач?
✓ Над чем нужно поработать дома?
VIII. Домашнее задание: Решить задачу на использование метода перекрывающихся площадей. Дан выпуклый четырехугольник ABCD. Середины сторон АВ и CD обозначены соответственно через К и М, точку пересечения отрезков ВМ и СК – через Р, точку пересечения отрезков АМ и DК – через О. Докажите, SMOKP = S▲BPC + S▲AOD.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.