Определение функции. Способы задания функций.
Виды функций. Свойства функции.
1. Определение: Функцией называется зависимость величины у от величины х, если каждому рассматриваемому значению величины х соответствует определенное значение величины у.
, где х – независимая переменная (аргумент); у – зависимая
переменная (значение функции).
2. Виды функций
- Целые
функции 
, где Р(х) – многочлен.
Пример: 
;
- Дробно-рациональные функции 
. Пример: 
;
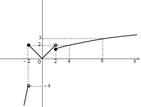
-Кусочные. Функция, которая
задается формулами, действующими на различных участках изменения аргумента.
Пример: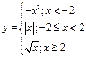
. График (см. рисунок)
- Обратимые. Функция называется
обратимой, если разным значениям аргументов из области определения функции
отвечают разные значения функции. Условие обратимости 
.
Пример: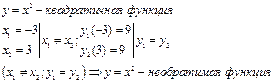
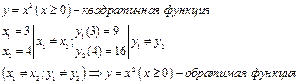
- Обратные. Для обратимой функции
определяется обратная функция
. Пример: Найти
обратную функцию для функции 
.
|
Этапы |
Решение |
|
1. Перенесем х в левую часть равенства, а у - в правую. Получаем уравнение. |
|
|
2. Решаем уравнение относительно переменной х. |
|
|
3. Производим замену |
|
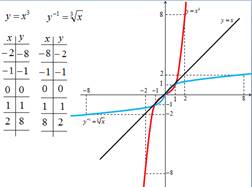Построим графики
функций 
и 
в
одной координатной плоскости.
Графики функций 
и
симметричны относительно прямой
у=х. Вывод: графики взаимнообратных функций симметричны
относительно прямой у=х.
- Сложные. Если 
, а 
,
то функция 
. Пример: 
-сложная функция, которую можно
разложить по функциям:
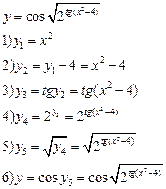
3. Способы задания табличный – таблицей; аналитический – формулами; графический - графиками; словесный – словами; полуграфический – смешанное задание.
Графиком функции называется множество всех точек координатной плоскости, абсциссами которых являются значения аргументов, а ординатами – соответствующие значения функции.
Утверждение: Для того, чтобы линия была графиком некоторой функции, необходимо и достаточно, чтобы всякая прямая параллельная оси ординат пересекала ее в одной точке.
4. Свойства функций.
|
№ |
свойства |
определение |
Математическая запись |
|
1 |
Область определения
Область значений |
|
|
|
2 |
Четность, нечетность |
Функция называется четной, если противоположным значениям аргументов соответствует одно и то же значение функции. Признак: графики четных функций симметричны относительно оси ординат.
Функция называется нечетной, если противоположным значениям аргументов соответствуют противоположные значения функции. Признак: графики нечетных функций симметричны относительно начало координат. |
|
|
3 |
Периодичность |
Функцию называют периодической с период Т не равным нулю, если для любых аргументов из области определения функции значения этой функции в точках х; х+Т; х-Т равны. |
|
|
4 |
Возрастание и убывание |
Функцию называют возрастающей (убывающей) на множестве Х, если на этом множестве при увеличении аргументов увеличиваются (уменьшаются) значения функции. Интервалы, на которых функция только возрастает или же только убывает называются интервалами монотонности. |
|
|
5 |
Ограниченность |
Функцию называют ограниченной снизу (сверху) на множестве Х, если существует такое число M, что на этом множестве значения функции превосходят (не превосходят) данное число M Функцию называют неограниченной на множестве Х, если для любого числа M найдется такой аргумент данной функции, что значение функции в этом аргументе по модулю строго больше этого числа M. |
|
|
6 |
Нули функции |
Это значения аргументов, в которых значения функции обращаются в нуль. Признак: график функции пересекает ось абсцисс.
|
|
|
7 |
Знакопостоянство |
Нули функции разбивают область определения на промежутки, в каждом из которых функция сохраняет постоянный знак. |
|
|
8 |
Точки экстремума (максимум и минимум) |
Точка х0 называется точкой минимума функции, если для всех х взятых из некоторой окрестности точки х0, значения функции в этих точках больше или равно значений функции в точке х0.
Точка х0 называется точкой максимума функции, если для всех х взятых из некоторой окрестности точки х0, значения функции в этих точках меньше или равно значений функции в точке х0.
|
|
|
9 |
Непрерывность |
|
|
|
10 |
Асимптоты |
|
|
Определение функции. Способы задания функций
Способы задания табличный – таблицей; аналитический – формулами; графический - графиками; словесный – словами; полуграфический – смешанное задание
Периодичность Функцию называют периодической с период
Знакопостоянство Нули функции разбивают область определения на промежутки, в каждом из которых функция сохраняет постоянный знак
© ООО «Знанио»
С вами с 2009 года.
