Методическая разработка урока "Показательная и логарифмическая функции"

ТЕМА ЛЕКЦИИ. Показательная и логарифмическая функции

Показательная функция, ее свойства и график

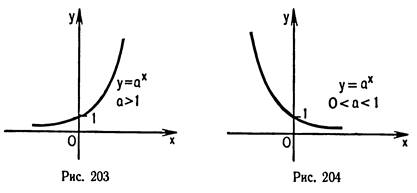
1.     Функция, заданная формулой вида , где а – некоторое положительное число, не равное единице, называется показательной. Число а называется основанием показательной функции, х – показатель.

2.     Функция  при  обладает следующими свойствами: 1) область определения – множество всех действительных чисел; 2) множество значений – множество всех положительных чисел; 3) функция возрастает на всей области определения; 4) при  значение функции равно 1; 5) если , то ;

6) если , то .

3.     Функция  при  обладает следующими свойствами: 1) область определения – множество всех действительных чисел; 2) множество значений – множество всех положительных чисел; 3) функция возрастает на всей области определения; 4) при  значение функции равно 1; 5) если , то ;

6) если , то .

4.     Показательная функция с основанием, равным иррациональному числу е  

(), то есть  называется экспонентой.

5.     Показательные функции применяются в биологии, физике, химии, социологии и других науках.

Обратная функция

1.     Пусть функция  монотонна (возрастает или убывает) в своей области определения . Тогда каждому значению соответствует единственное значение  и обратно: каждому значению  соответствует единственное значение . Значит, в этом случае можно построить новую функцию, определенную на  и такую, что каждому  ставится в соответствие , удовлетворяющее уравнению . Эта новая функция называется обратной по отношению к функции .

2.     Для нахождения функции, обратной данной , надо выразить х через у: , а затем записать полученную функцию в общепринятой форме . Например, если дана функция , то обратная этой функция будет иметь вид  или .

3.     Если функции  и  являются взаимно обратными, то область определения функции  совпадает с множеством значений функции  и, наоборот, область определения функции  совпадает с множеством значений функции , то есть  и .

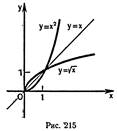
4.     Графики взаимно обратных функций симметричны относительно прямой  (рис. 214)

5.     Рассмотрим, например, функцию , заданную на промежутке . На этом промежутке функция убывает и принимает все значения из множества . Следовательно, для данной функции существует обратная. Из уравнения  находим  и ; так как переменная х может принимать только неположительные значения, то искомая обратная функция имеет вид . Поменяв обозначения х на у и у на х, получим формулу , где , с помощью которой и задается обратная функция. Если же рассматривать функцию , заданную на промежутке , то обратной для нее служит функция , где . На рисунке 215 изображены график функции  при  и график обратной ей функции.

Понятие логарифма

1.     Логарифмом положительного числа b по основанию а (где , ) называется показатель степени, в которую надо возвести а, чтобы получилось число b. Логарифм числа b по основанию а обозначается символом . Определение логарифма символически можно записать так: .

2.     Если , , , то  по определению есть показатель степени, в которую надо возвести число а, чтобы получить число b. Поэтому равенство  есть тождество, которое называют основным логарифмическим тождеством. Например, , .

3.     Наиболее распространенные в инженерной, экономической и статистической практике десятичные и натуральные логарифмы (с основаниями соответственно 10 и е) получили собственные обозначения: , .

Вычислить: , , , .

Свойства логарифмов

1.     Логарифмы существуют только для положительных чисел, то есть  (где , ) существует, если .

2.     При основании  логарифмы чисел  положительны, а логарифмы чисел  отрицательны. Например, , .

3.     При основании  логарифмы чисел  отрицательны, а логарифмы чисел  положительны. Например, , .

4.     Равным положительным числам соответствуют и равные логарифмы, то есть, если , то .

5.     Если , то большему числу соответствует и больший логарифм, то есть если , то . Например, .

6.     Если , то большему числу соответствует меньший логарифм, то есть если , то . Например, .

7.     Логарифм единицы по любому основанию (, ) равен нулю, то есть .

8.     Логарифм самого основания равен 1, то есть .

Теоремы о логарифме произведения, частного и степени, формула перехода к новому основанию

1.     Логарифм произведения двух или нескольких положительных чисел равен сумме логарифмов сомножителей, то есть  (, , , ). Например, .

2.     Логарифм частного положительных чисел равен разности логарифмов делимого и делителя, то есть  (, , , ). Например, .

3.     Логарифм степени равен произведению показателя этой степени на логарифм ее основания, то есть , где , , .

4.     Формула перехода к от основания b к основанию а имеет вид: , где , , , , . Например, .

5.     Если , то формула перехода примет вид: , или , где , , , . Например, .

6.     Если основание логарифма и число, стоящее под знаком логарифма, возвести в одну и ту же степень, отличную от нуля, то значение логарифма не изменится: , где , , ; , , , , . Например, .

Найти , если  и .

Логарифмирование и потенцирование

1.     Логарифмирование – это преобразование, при котором логарифм выражения с переменными приводится к сумме или разности логарифмов переменных.

2.     Необходимо четко различать сумму логарифмов  и логарифм суммы . Сумма логарифмов равна логарифму произведения, то есть , а для логарифма суммы формулы нет. Например, Дано , , , . Найти . Решение: .

3.     Потенцирование – это преобразование, обратное логарифмированию. Например, дано , , , . Найти . Решение: , .

Логарифмическая функция, её свойства и график

1.     Так как показательная функция  (где , ) является монотонной (возрастающей при  и убывающей при ), то она имеет обратную функцию. Чтобы найти эту обратную функцию, нужно из формулы  выразить х через у: , а затем поменять обозначения х на у и у на х; тогда получим . Функция  (где , ) называется логарифмической. Итак, показательная и логарифмическая функции при одном и том же основании являются взаимно обратными функциями.

2.     График логарифмической функции  можно построить, воспользовавшись тем, что функция  обратна показательной функции . Поэтому достаточно построить график функции , а затем отобразить его симметрично относительно прямой . На рисунке 217 изображен график функции  при , на рисунке 218 – график функции  при .

3.     Свойства функции  при : 1) ; 2) ; 3) функция возрастает; 4) если , то ; 5) если , то ; 6) если , то .

4.     Свойства функции  при : 1) ; 2) ; 3) функция убывает; 4) если , то ; 5) если , то ; 6) если , то .

Показательные уравнения

1.     Уравнение, содержащее переменную в показателе степени, называется показательным. Простейшим примером показательного уравнения служит уравнение , где , . Это уравнение можно решить графически (рис. 213).

2.     Решение показательного уравнения вида , где , , основано на том, что это уравнение равносильно уравнению .

3.     Уравнение вида  с помощью подстановки ,  сводится к квадратному уравнению .

4.     Уравнение вида  называется однородным уравнением первого порядка. Такие уравнения решают делением на любую из функций: . Тогда .

Например: решить уравнения: 1) ; 2) ; 3) .

Показательные неравенства

1.     Неравенство, содержащее переменную в показателе степени, называется показательным.

2.     Решение показательных неравенств вида , где , , основано на следующих утверждениях: 1) если , то неравенства  и  равносильны; 2) если , то неравенства  и . Это следует из того, что при  показательная функция возрастает, а при  убывает.

Например: решить неравенства 1) ; 2) .

Логарифмические уравнения

1.     Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим. Простейшим примером логарифмического уравнения служит уравнение , где , . Такое уравнение решается по определению логарифма: .

2.     Решение логарифмического уравнения вида  основано на том, что такое уравнение равносильно уравнению  при дополнительных условиях  и .

3.     Переход от уравнения  к уравнению  иногда приводит к появлению посторонних корней. Такие корни можно выявить либо с помощью подстановки найденных корней в исходное логарифмическое уравнение, либо с помощью нахождения области определения исходного уравнения. Эта область задается системой неравенств

4.     При решении логарифмических уравнений часто бывает полезен метод введения новой переменной.

5.     при решении уравнений, содержащих переменную и в основании, и в показателе степени, используется метод логарифмирования. Если при этом в показателе степени содержится логарифм, то обе части уравнения нужно прологарифмировать по основанию этого логарифма.

Например: решить уравнения 1) ; 2) ; 3) .

Логарифмические неравенства

1.     Неравенство, содержащее переменную под знаком логарифма, называется логарифмическим. Например, неравенства ,  при ,  называются логарифмическими.

2.     Неравенство  равносильно системе  при  и системе  при .

3.     При решении логарифмических неравенств следует учитывать общие свойства неравенств, свойство монотонности логарифмической функции и область ее определения.

Например: решить неравенства 1) ; 2) ; 3) ; 4) .