ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ АДМИИСТРАЦИИ ВЛАДИМИРСКОЙ ОБЛАСТИ

ГБПОУ ВО«Владимирский политехнический колледж»

УТВЕРЖДАЮ

Зам. директора по УМР

________________ Е.В. Михайлова

«___»___________________2019 г.

Методические указания

по выполнению контрольной работы

по дисциплине

ЕН.01. МАТЕМАТИКА

для студентов заочного отделения по специальности

09.02.05 «Прикладная информатика (по отраслям)»

2019

Составитель:           Штучкина Т.С. – преподаватель

 ГБПОУ ВО «Владимирский политехнический колледж»

Рецензенты:         Королева С.А. – преподаватель

 ГБПОУ ВО «Владимирский политехнический колледж»

Жукова И. В. – преподаватель математики

 ГБПОУ ВО «Владимирский строительный колледж»

Аннотация

Методические указания по выполнению контрольной работы  предназначены для реализации учебного процесса в ГБПОУ ВО «Владимирский политехнический колледж». Они включают в себя: содержание учебной дисциплины,  задания для выполнения контрольной работы, образец выполнения контрольной работы, критерии оценки работы.

Методические указания по выполнению контрольной работы предназначены  для студентов 1 курса заочного отделения по специальности 09.02.05 «Прикладная информатика (по отраслям)».

Оглавление

Аннотация. 3

ВВЕДЕНИЕ. 5

1 Методические указания по выполнению контрольной работы. 6

2    Задания для выполнения  контрольной работы. 8

3    Образец выполнения контрольной работы.. 12

4  Критерии оценивания практической работы.. 20

ЗАКЛЮЧЕНИЕ. 21

Список используемой литературы.. 22

ПРИЛОЖЕНИЕ А.. 23

ВВЕДЕНИЕ

Контрольная работа  –  одна из основных форм проверки знаний, выполненная в соответствии с учебным планом, способствующая закреплению теоретических знаний и формирующая у студентов дополнительные навыки самостоятельного анализа теории и практики.

Контрольная работа представляет собой письменный ответ на вопрос (решение задачи или выполнение конкретного задания), который рассматривается  в пределах одной или нескольких тем учебной дисциплины.

Содержание ответа на поставленный вопрос включает демонстрацию автором знания теории вопроса и понятийного аппарата, понимание существующей практики.

Цель контрольной работы – закрепление практических навыков применения теоретических подходов и методов анализа на учебных примерах и задачах.

Задачи, стоящие перед студентом во время выполнения контрольной работы:

-     изучение научной, учебной, справочной литературы по определенному вопросу;

-     самостоятельный анализ основных теоретических положений и теорий отечественных и зарубежных специалистов;

-     умение применять теоретические знания на практике.

При выполнении контрольной  работы студент должен  проявить способности к научно-исследовательской работе, используя при этом знания, полученные в процессе изучения дисциплины, предусмотренные рабочей программой.

1 Методические указания по выполнению контрольной работы

Студенты заочной формы обучения выполняют одну контрольную работу.

1.    Контрольная работа выполняется в отдельной тетради с нумерацией страниц и соблюдением полей для замечаний рецензентов. Текст рукописный (подчерк разборчивый). 

2.    На обложке тетради должен быть приклеен титульный лист утвер­жденного образца или аккуратно записаны все данные титульного листа: шифр, специальность, если она не отражена в шифре, фами­лия, имя, отчество студента, предмет и номер работы.

3.    При выполнении  контрольной работы, прежде всего, надо переписать условие задачи, дать подробное решение.

4.    Выполненная работа направляется на проверку и рецензирование. При положительной рецензии студент допускается к собеседованию, в ходе которого проверяются его знания и умения по решенным заданиям. В случае отрицательной рецензии контрольная работа возвращается студенту для доработки. При повторном представлении работы на проверку прилагается и первоначальный вариант с рецензией.

5.    Собеседование по контрольной работе проводится во время экзаменационной сессии в предусмотренное расписанием время. Студент может прийти на собеседование к преподавателю и в другое время в течение межсессионного периода в часы индивидуальных консультаций преподавателя.

6.    Студент должен выполнить вариант контрольной работы в соответствии с таблицей 1, контрольные задания по вариантам распределены в таблице 2.

Таблица 1. – Распределение вариантов  контрольной  работы.

Таблица 2. –  Распределение заданий контрольной работы по вариантам.

Собеседование по контрольной работе проводится по вопросам, указанным в ПРИЛОЖЕНИЕ А.

2        Задания для выполнения  контрольной работы

1.                     Решите систему уравнений методом Крамера.

1.          

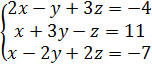
2.          

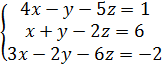
3.            

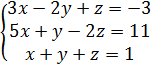
4.          

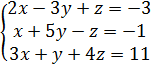
5.          

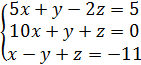
2.                     Вычислите пределы функций:

3.                     Исследуйте функцию и постройте её график:

11.

12.

13.

14.

15.

4.  Вычислите площадь фигуры, ограниченной параболой с  и прямой . Сделайте чертеж:

ПРИЛОЖЕНИЕ А

Список вопросов для собеседования по контрольной работе.

1.       Матрицы. Виды матриц. Операции над матрицами.

2.       Определители: виды, приемы вычисления

3.       Методы  решения  систем  линейных  уравнений:  метод  Крамера,  Метод Гаусса.

4.       Предел и непрерывность функции. Неопределенности.

5.       Производная. Правила дифференцирования.

6.       Приложения дифференциального исчисления.

7.       Первообразная. Неопределенный интеграл.

8.       Правила интегрирования. Таблица основных интегралов.

9.       Основные методы интегрирования: непосредственное интегрирование, замена переменной, интегрирование по частям.

10.    Определенный интеграл. Геометрический смысл. Формула Ньютона-Лейбница для вычисления определенного интеграла.

11.   Методы вычисления определенного интеграла: заменой переменной, по частям.

12.   Вычисление площади определенным интегралом.

13.   Вероятность события. Свойства вероятности

14.   Теоремы сложения и умножения вероятностей.

15.   Дискретная случайная величина. Числовые характеристики ДСВ.

16.   Эмпирическая функция распределения.

17.   Полигон и гистограмма.

18.   Числовые характеристики выборки.

19.   Понятие комплексного числа. Модуль комплексного числа.

20.   Операции с комплексными числами.

Скачано с www.znanio.ru