
Одной из форм организации внеклассной работы по предмету является проведение недели математики, которая включает в себя различные конкурсы и состязания, а также уроки математики, проводимые в нестандартных формах.
Целям и задачам недели математики соответствует нестандартный урок «Математические софизмы».
Трудно, изучая математику, не заинтересоваться математическими софизмами. В 2003 году в издательстве Просвещение вышла книга А.Г. Мадеры и Д.А. Мадеры «Математические софизмы», в которой более восьмидесяти математических софизмов, по крупицам собранным из различных источников. «Математический софизм представляет собой, по существу, правдоподобное рассуждение, приводящее к неправдоподобному результату. Причем полученный результат может противоречить всем нашим представлениям, но найти ошибку в рассуждении зачастую не так-то просто; иной раз она может быть и довольно тонкой и глубокой. Поиск заключенных в софизме ошибок, ясное понимание их причин ведут к осмысленному постижению математики. Обнаружение и анализ ошибки, заключенной в софизме, зачастую оказываются более поучительными, чем просто разбор решений «безошибочных» задач. Эффектная демонстрация «доказательства» явно неверного результата, в чем и состоит смысл софизма, демонстрация того, к какой нелепице приводит пренебрежение тем или иным математическим правилом, и последующий поиск и разбор ошибки, приведшей к нелепице, позволяют на эмоциональном уровне понять и «закрепить» то или иное математическое правило или утверждение. Такой подход при обучении математике способствует более глубокому ее пониманию и осмыслению».[1]
ЦЕЛЬ УРОКА
Ø Развитие логического мышления учащихся, их познавательного интереса.
Ø Раскрыть содержание понятия софизма;
Ø совершить экскурс в историю софизмов;
Ø решить ряд математических софизмов и разобрать ошибки в их решении.
Ø Плакаты с высказываниями о математике.
Ø Презентация Power Point.
(Песенка английских студентов)
Чем больше учишься, тем больше знаешь.
Чем больше знаешь, тем больше забываешь...
Чем больше забываешь, тем меньше знаешь...
Чем меньше знаешь, тем меньше забываешь.
Но чем меньше забываешь, тем больше знаешь.
Так для чего учиться?
Думаю, многие хотя бы раз в жизни слышали подобные высказывания: «Все числа равны» или «два равно трём». Таких примеров может быть очень много, но что же это значит? Кто это придумал? Можно-ли как-то объяснить эти высказывания или всё это – вымысел?
На эти вопросы, и на многие другие мы и ответим на нашем занятии «Математические софизмы».
Софизмом называется умышленно ложное умозаключение, которое имеет видимость правильного. Каков бы ни был софизм, он обязательно содержит одну или несколько замаскированных ошибок. Особенно часто в математических софизмах выполняются «запрещенные» действия или не учитываются условия применимости теорем, формул и правил. Иногда рассуждения ведутся с использованием ошибочного чертежа или опираются на приводящие к ошибочным заключениям «очевидности». Встречаются софизмы, содержащие и другие ошибки.
В истории развития математики софизмы играли существенную роль. Они способствовали повышению строгости математических рассуждений и содействовали более глубокому уяснению понятий и методов математики. Роль софизмов в развитии математики сходна с той ролью, какую играют непреднамеренные ошибки в математических исследованиях, допускаемые даже выдающимися математиками.
Софистами называли группу древнегреческих философов 4-5 века до н.э., достигших большого искусства в логике. В период падения нравов древнегреческого общества (5 век) появляются так называемые учителя красноречия, которые целью своей деятельности считали и называли приобретение и распространения мудрости, вследствие чего они именовали себя софистами. Наиболее известна деятельность старших софистов, к которым относят Протагора из Абдеры, Горгия из Леонтип, Гиппия из Элиды и Продика из Кеоса. Но суть деятельности софистов много больше, чем простое обучение искусству красноречия. Они обучали и просвещали древнегреческий народ, старались способствовать достижению нравственности, присутствия духа, способности ума ориентироваться во всяком деле. Но софисты не были учеными. Умение, которое должно было быть достигнуто с их помощью, заключалось в том, что человек учился иметь в виду многообразные точки зрения.
Аристотель называл софизмом «мнимые доказательства», в которых обоснованность заключения кажущаяся и обязана чисто субъективному впечатлению, вызванному недостаточностью логического анализа. Убедительность на первый взгляд многих софизмов, их «логичность» обычно связана с хорошо замаскированной ошибкой — семиотической: за счёт метафоричности речи, нарушающих однозначность мысли и приводящих к смешению значений терминов, или же логической: подмена основной мысли (тезиса) доказательства, принятие ложных посылок за истинные, несоблюдение допустимых способов рассуждения (правил логического вывода), использование «неразрешённых» или даже «запрещённых» правил или действий, например деления на нуль в математических софизмах.
Исторически с понятием «софизм» неизменно связывают идею о намеренной фальсификации, руководствуясь признанием Протагора, что задача софиста (софист, от греч. sophistes — умелец, изобретатель, мудрец, лжемудрец) — представить наихудший аргумент как наилучший путём хитроумных уловок в речи, в рассуждении, заботясь не об истине, а об успехе в споре или о практической выгоде. С этой же идеей обычно связывают и «критерий основания», сформулированный Протагором: мнение человека есть мера истины. Так, софизм «куча» («Одно зерно — не куча. Если n зёрен не куча, то n + 1 зерно — тоже не куча. Следовательно, любое число зёрен — не куча») — это лишь один из «парадоксов транзитивности», возникающих в ситуации «неразличимости».
«Правильно понятая ошибка – это путь к открытию». – Сказал Иван Петрович Павлов
(1849–1936) — выдающийся учёный, гордость отечественной науки, «первый физиолог мира», как назвали его коллеги на одном из международных съездов. И действительно, уяснение ошибок в математических рассуждениях часто содействовало развитию математики.
Пожалуй, особенно поучительна в этом отношении история аксиомы Евклида о параллельных прямых. Сформулировать эту аксиому можно так: через данную точку, лежащую вне данной прямой, можно провести не более одной прямой, параллельной данной (что одну прямую, параллельную данной, можно провести – это доказывается). Это утверждение на протяжении более чем двух тысяч лет пытались доказать, т.е. вывести из остальных аксиом геометрии, многие выдающиеся математики разных времен и разных народов. Все эти попытки не увенчались успехом. Многочисленные доказательства, какие были найдены, оказались ошибочными. Пытался доказать эту аксиому и наш великий соотечественник Н.И. Лобачевский, но скоро понял, что этого сделать нельзя. Путь, идя которым Лобачевский убедился в этом, привел его к созданию новой неевклидовой геометрии.
Примеров такого рода можно было бы привести несколько.
Чем же полезны софизмы для изучающих математику? Что они могут дать?
Разбор софизмов, прежде всего, развивает логическое мышление, т.е. прививает навыки правильного мышления. Обнаружить ошибку в софизме – это, значит, осознать ее, а осознание ошибки предупреждает от повторения ее в других математических рассуждениях. Когда ребенок раз притронется к горячему предмету, то впоследствии он постарается этого не делать. Он будет много осторожнее. Так изучающий математику впоследствии проявит больше осторожности.
Далее, что особенно важно, разбор софизмов помогает сознательному усвоению изучаемого материала, развивает наблюдательность, вдумчивость и критическое отношение к тому, что изучается. Математические софизмы приучают внимательно и настороженно продвигаться вперед, тщательно следить за точностью формулировок, правильностью записей и чертежей, за допустимостью обобщений, за законностью выполняемых операций. Все это нужно и важно.
Развитие критического мышления позволит не только успешно освоить точные науки, но и не оказаться жертвой мошенников в жизни. Например, при оформлении кредита в банке не оказаться пожизненным его должником.
Наконец, разбор софизмов увлекателен. Только очень сухого человека не может увлечь интересный софизм. Как приятно бывает обнаружить ошибку в математическом софизме. И тем как бы восстановить истину в ее правах. И чем труднее софизм, тем большее удовлетворение доставляет его анализ. Очень важно добиться отчетливого понимания ошибок, иначе софизмы будут бесполезны.
Ø Запрещенные действия;
Ø пренебрежение условиями теорем; формул и правил;
Ø ошибочный чертеж;
Ø опора на ошибочные умозаключения.
Успешность софизма определяется следующей формулой:
a + b + c + d + e + f, где (a + с + е) составляет показатель силы диалектики, (b + d + f)
есть показатель слабости его жертвы.
Ø а - отрицательные качества лица (отсутствие развития способности управлять вниманием).
Ø b - положительные качества лица (способность активно мыслить).
Ø с - аффективный элемент в душе искусного диалектика.
Ø d - качества, которые пробуждаются в душе жертвы софиста и омрачают в ней ясность мышления.
Ø е - категоричность тона, не допускающего возражения, определённая мимика.
Ø f - пассивность слушателя.
Ø Алгебраические софизмы – ошибки в числовых выражениях и уравнениях, скрытые намеренно.
Ø Арифметические софизмы – выражения чисел, имеющие ошибку, незаметную с первого взгляда.
Ø
Геометрические ![]() – умозаключение, заведомо
неправильное, которое касается геометрических фигур и действий над ними;
– умозаключение, заведомо
неправильное, которое касается геометрических фигур и действий над ними;
Ø Кроме математических, существует множество других видов софизмов: исторические, терминологические, психологические, логические и т.д. Абсурдность таких рассуждений гораздо проще понять и разоблачить. Некоторые утверждения выглядят несерьезными и наивными, лишенными смысла и цели, недосказанными.
АЛГЕБРАИЧЕСКИЕ СОФИЗМЫ
Докажем, что 5 = 6.
Запишем равенство: 35 + 10 − 45 = 42 + 12 − 54 .
Вынесем за скобку общие множители: 5 ∙ (7 + 2 − 9) = 6 ∙ (7 + 2 − 9).
Разделим обе части этого равенства на общий множитель, заключенный в скобках. Получаем 5 = 6. В чем ошибка?
Ответ: Нельзя делить на 7 + 2 – 9 = 0.
Имеем числовое равенство (верное): 4 : 4 = 5 : 5.
Вынесем за скобки в каждой части его общий множитель. Получим: 4(1 : 1) = 5(1 : 1). Числа в скобках равны, поэтому 4 = 5, или 2 2 = 5.
Ответ: Ошибка допущена в вынесении общего множителя за скобки в левой и правой частях тождества 4 : 4 = 5 : 5.
Имеем числовое равенство 𝑥 − 𝑎 = 0.
![]() Разделим обе части на 𝑥 − 𝑎
, 𝑥−𝑎 = 0 .
Разделим обе части на 𝑥 − 𝑎
, 𝑥−𝑎 = 0 .
𝑥−𝑎 𝑥−𝑎
Получим требуемое равенство 1 = 0.
Ответ: Ошибка допущена в делении на выражение 𝑥 − 𝑎 = 0 . Делить на 0 нельзя!
Докажем, что 4 = 5.
Где допущена ошибка в следующей цепочке равенств:
16 − 36
= 25 − 45,16 − 36 + 20 ![]() = 25 − 45 + 20
= 25 − 45 + 20 ![]() ,
,
9 2 9 2
![]()
![]() (4 − ) = (5 − )
, 4 −= 5 −, 4 = 5?
(4 − ) = (5 − )
, 4 −= 5 −, 4 = 5?
2 2
9 2 9 2
![]()
![]() Ответ:
(4 −
Ответ:
(4 − ![]() ) = (5 − ) < = >
|4 − | = |5 − |.
) = (5 − ) < = >
|4 − | = |5 − |.
2 2
Желая доказать, что 5 = 1, будем рассуждать так:
из чисел 5 и 1 по отдельности вычтем одно и то же число 3.
Получим числа 2 и – 2.
При возведении в квадрат этих чисел получаются равные числа 4 и 4.
Значит, должны быть равны и исходные числа 5 и 1. Где ошибка?
Ответ: Из равенства квадратов двух чисел не следует, что сами эти числа равны.
Возьмем два равных числа а и с, а = с.
Обе части этого равенства умножим на а и затем вычтем из произведений по с2.
Получим: а2 – с2 = ас – с2, или (а + с)(а – с) = с(а – с). Отсюда, а + с = с, или, а + а = а, т.к. по условию, а = с. а
Значит, 2а = а, или, а = .
2
Какая ошибка допущена в этих рассуждениях?
Ответ: Нельзя делить на а – с, так как а – с = 0.
Отрицательное число больше положительного Возьмем два положительных числа 𝑎 и 𝑏. Сравним два отношения: 𝑎 и −𝑎. Они равны,
−𝑏 𝑏
![]() так как
каждое из них равно − 𝑎
так как
каждое из них равно − 𝑎![]() . Можем составить пропорцию: 𝑎 = −𝑎.
Но если в
. Можем составить пропорцию: 𝑎 = −𝑎.
Но если в
𝑏 −𝑏 𝑏
пропорции предыдущий член первого отношения больше последующего, то предыдущий член второго отношения также больше своего последующего. В нашем случае 𝑎 > −𝑏; следовательно, должно быть −𝑎 > 𝑏, т.е. отрицательное число больше положительного. В чем ошибка?
Ответ: Свойство: если в пропорции предыдущий член первого отношения больше последующего, то и предыдущий член второго отношения больше своего последующего – может оказаться неверным, если некоторые члены пропорции отрицательны.
ГЕОМЕТРИЧЕСКИЕ СОФИЗМЫ
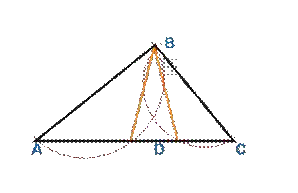
Попытаемся «доказать», что через точку, лежащую вне прямой, к этой прямой можно провести два перпендикуляра. С этой целью возьмем треугольник АВС (рис. 1). На сторонах АВ и ВС этого треугольника, как на диаметрах, построим полуокружности. Пусть эти полуокружности пересекаются со стороной АС в точках Е и D. Соединим точки Е и D прямыми с точкой В. ⦟АЕВ = 90°, как вписанный, опирающийся на диаметр; ⦟ 𝐵𝐷𝐶 = 90° прямой. Следовательно, ВЕ АС и ВD АС. Через точку В проходят два перпендикуляра к прямой АС. В чем ошибка?
Ответ: Рассуждения опирались на ошибочный чертеж. В действительности полуокружности пересекались со стороной АС в одной точке, т.е. ВЕ совпадает с ВD.
Ø «Сидящий встал; кто встал, тот стоит; следовательно, сидящий стоит».
Ø «Сократ - человек; человек - не то же самое, что Сократ; значит, Сократ - это нечто иное, чем Сократ».
Ø «Для того чтобы видеть, вовсе необязательно иметь глаза, ведь без правого глаза мы видим, без левого тоже видим; кроме правого и левого, других глаз у нас нет; поэтому ясно, что глаза не являются необходимыми для зрения».
Ø «Рога». Ты имеешь то, что не терял. Ты не потерял рога, значит, они у тебя есть.
Ø «Лгун». Есть вероятность, что лгун сознается в том, что он обманщик. Значит, он скажет правду. Тот, кто говорит правду, лгуном не является. Значит, лгун – совсем не лгун.
Ø «Лекарства». Лекарства, принимаемые больным – это добро. Делать добра нужно как можно больше. Соответственно, нужно принимать много лекарств.
О математических софизмах можно говорить бесконечно долго, как и о математике в целом. Каждый день придумываются новые парадоксы, при этом не забываются старые, придуманные учёными много веков назад.
Понять софизм как таковой (решить его и найти ошибку) получается не сразу. Требуются определенный навык и смекалка. Но ясно одно: СОФИСТИКА – это целая наука, а именно математические софизмы – это лишь часть одного большого течения
1. Ахманов А. С., «Логическое учение Аристотеля», М., 1960;
2. Мадера А.Г., Мадера Д.А. «Математические софизмы», М.: Просвещение, 2003;
3. Нагибин Ф.Ф., Канин Е.С. «Математическая шкатулка», Просвещение, 1984;
4. Обреимов В.И., «Математические софизмы», СПб, 1989;
5. Картинки [Электронный ресурс] URL: http://go.mail.ru/ (дата обращения: январь 2013).
6. Научное издательство «Большая Российская энциклопедия» / Большая Советская энциклопедия – М.: «Новый Диск», 2003. – ил.
7. http://ru.wikipedia.org/wiki/Софизм
8. http://slovari.yandex.ru/
9. «Большая энциклопедия Кирилла и Мефодия» - М.: «Кирилл и Мефодий», 2004. – ил.
10. http://www.sunhome.ru/philosophy/1749.
[1] Мадера А.Г., Мадера Д.А. «Математические софизмы», М.: Просвещение, 2003.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.