Обобщающий урок алгебры в 9 классе на тему

"Степенная функция»

Образовательные цели урока.

·         Повторить и обобщить знания обучающихся по теме «Степенная функция»

Развивающие цели урока.

·         Развивать творческую и мыслительную деятельность учащихся, их интеллектуальные качества: способность к «видению» проблемы.

·         Формировать умение четко и ясно излагать свои мысли.

·         Развивать пространственное воображение учащихся.

План урока.

1. Организация начала урока.
2. Разминка.
3. Устная работа.
4. Самостоятельная работа.
5. Тестовая работа.
6. Подведение итогов урока.
7. Задание на дом.

Ход урока

1.      Организация начала урока.

Каждый учащийся получает маршрутный лист, в котором отмечены все этапы урока и куда будут заноситься все результаты на каждом этапе.

В начале урока, в беседе учащимся сообщается тема урока, цели, задачи и план проведения урока.

2. Разминка.

В качестве разминки ребятам предлагается кроссворд. 

3. Устная работа.

Устная работа проектируется на экран с помощью проектора, за каждый правильно данный ответ учащиеся получают жетон, общее количество которых заносится в маршрутный лист, и в дальнейшем будет влиять на оценку за урок.

Исследуйте функцию на четность:

а)     Ответ: четная          б) 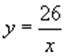 Ответ: нечетная    

в) Ответ: ни четная,  ни нечетная

Укажите график нечетной функции

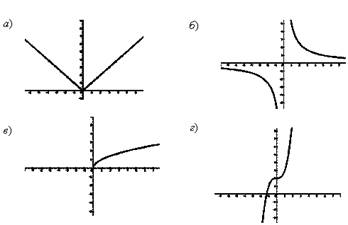Ответ:  б

1.      Есть ли среди предложенных график четной функции?   Ответ: а

2.      Что можно сказать о функции на рисунке под буквой в)? Ответ: ни четная,  ни нечетная

3.      Функция - четная, и , . Чему равно значение ? ?  (Ответ: >)

4.      Может ли быть нечетной функция, область определения которой – промежуток ?      Ответ: нет

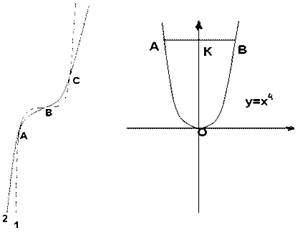
5.      Витя Верхоглядкин начертил график функции и , а потом стер оси координат. Назовите координаты точек А, В и С. Графиком какой функции является линия 1, линия 2?

Ответ: А(-1;-1), В(0;0), С(1;1), линия 1 ; линия 2

6.      Найдите АВ, если ОК = 81 (Ответ: АК=КВ=3, значит АВ=6)

7.      Известно, что точки А(-3;-2), В(1;5), С(3;2) и М(-1;-5) принадлежат одному и тому же графику. Выясните, может ли эта функция быть четной, нечетной. Ответ: нечетной

4. Самостоятельная работа.

У каждого учащегося на столе есть текст работы, составленный на два варианта, таким образом, что каждый вопрос подразумевает только два ответа “да” или “нет”.

 (ответьте на каждый вопрос диктанта либо “да”, либо “нет”, и отметьте в бланке ответов при ответе “да” значок +, а при ответе “нет” — )

Вариант 1

1. Графиком функции является парабола
2. Областью определения функции являются все числа
3. Функция четная
4. Значение выражения
5. Если , то - четная.
6. является корнем уравнения .
7. При нечетном n уравнение имеет два корня.
8. Уравнение имеет два корня.
9. Точка А(-2;-32) принадлежит графику функции

Вариант 2

1. Областью определения функции являются все числа кроме .
2. Функция нечетная.
3. Точка А(-2; 32) принадлежит графику функции .
4. является корнем уравнения .
5. При четном n уравнение имеет два корня.
6. Если , то - нечетная.
7. Значение выражения .
8. Графиком функции является прямая.
9. Уравнение имеет два корня.

После того, как ребята ответят на все вопросы работы и внесут свои ответы в специально приготовленную таблицу в маршрутном листе, производится взаимопроверка работ по заранее приготовленным ответам, которые воспроизводятся на экране с помощью проектора.

Ответы на самостоятельную работу

1 вариант

2 вариант

Проверяющий сверяет ответы оппонента с предложенным ключом и вносит в графу оценка количество правильных ответов, например 8.

5.      Работа с тестами.

Выполняют тест в тетрадях, ответы на который заносятся в специально приготовленный бланк ответов в маршрутном листе. Ниже приведены задания этого теста на два варианта.

Тест №1                                                              Вариант 1

1. Какая из данных функций является четной?

а)                   б)                    в)               г)

2. На рисунке изображена часть графика четной функции, достроить график и выяснить, какая из данных точек принадлежит графику этой функции.

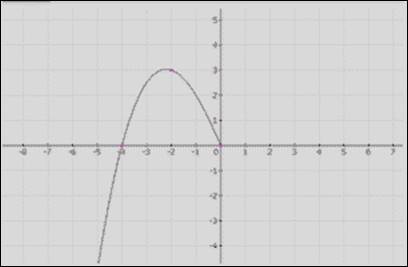
а) (3;2)         б) (2;3)         в) (-2;-3)      г) (2;-3)

3. Функция задана формулой . Сравните .

а)            б)            в)        г)

4. Функция задана формулой . Сравните .

а)                б)                    в)           г)

5. Какие из графиков имеют ось симметрии?

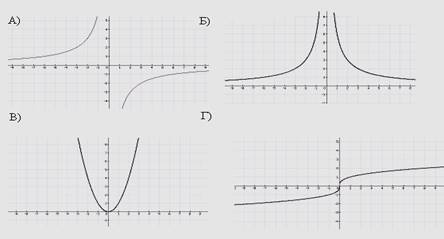
а) А и Б                          б) В и Б                  в) А и Г                        г) В и Г

6. . Функция – нечетная, - четная. Найдите .

 а) -10             б) 38                   в) 10                   г) -38

7.  - четная функция. Выберите ложное предложение

а)                                                             б) А(-3; 81) – принадлежит графику

в) уравнение имеет одно решение                      г)

8. Решите уравнение       

а) 2                     б) -2 и 2                      в) -2                     г) нет решений

Тест №1                                                       Вариант 2

1. Какая из данных функций является нечетной?

а)          б)          в)           г )

2. На рисунке изображена часть графика нечетной функции, достроить график и выяснить, какая из данных точек принадлежит графику этой функции.

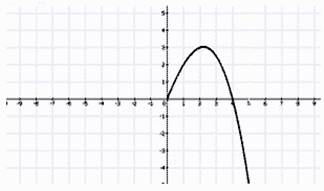
а) (-1;-2)              б) (-1;2)                 в) (-2;-1)                     г) (1;-2)

3. Функция задана формулой . Сравните .

а)       б)      в)     г)

4. Функция задана формулой . Сравните .

а)             б)           в)             г)

5. Какие из графиков имеют центр симметрии?

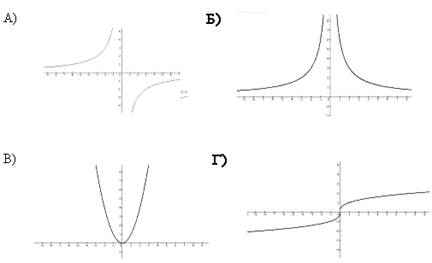
а) А и В                 б) Г и Б                  в) А и Г                        г) В и Б

6. . Функция – нечетная, - четная. Найдите .

а) 5                          б) 37                               в) -37                             г) -5

7. - нечетная функция. Выберите ложное предложение

а)                                                          б) А(-5; -125) – принадлежит графику

в) уравнение не имеет решение                г)

8. Решите уравнение

а) 2                 б) -2 и 2                  в) -2                        г) нет решений

После того как тест будет выполнен, как и на предыдущем этапе, ребята проводят взаимопроверку по заранее приготовленному ключу. Количество верно выполненных заданий вносится в графу оценка бланка ответов.

Ответы на тестовую работу

1 вариант

2 вариант

6. Подведение итогов урока.

В конце урока учащиеся сдают маршрутные листы учителю, и учитель выставляет общую оценку за урок каждому учащемуся.

7. Домашнее задание. Домашняя контрольная работа №3 стр. 91