Обратные тригонометрические функции, их свойства и графики

Сабақтың  жоспары

Поурочный  план

The  plan  of the  lesson

Күні/ Дата / Date :

Топ / Группа/ Group:

Пән / Предмет/Subject: Математика

Сабақтың  тақырыбы/Тема  занятия/Theme: «Обратные тригонометрические функции»

Сабақтың  үлгісі/ Тип  занятия /Typeofthelesson:  изучение нового материала, закрепление новых знаний

Сабақтың  түрі / Вид занятия / Kind  of  the  lesson: комбинированный урок

Мақсаты/  Цели  занятия / Objectives:

білімдік/образовательная / educational: дать определения арксинуса, арккосинуса, арктангенса, арккотангенса, построить графики этих функций, изучить свойства аркфункций, показать связь с тригонометрическими функциями; уметь находить значения обратных тригонометрических функций.

дамытушылық/  развивающая / developing: развивать логическое мышление, математическую речь, умение работать в нужном темпе, внимание

тәрбиелік/ воспитательная / bringing - up: воспитывать ответственность, аккуратность при построении графиков

Көрнекіқұралдар/ Oборудование / Resources: мультимедийный проектор; интерактивная доска; презентация, учебники

 

Сабақтың  барысы/ План занятия / Plan

 

1.Организационный  момент.

2. Актуализация знаний.

2.Целеполагание.

3. Ход занятия.

4. Итог.

6. Домашнее задание.

 

Ход  занятия

I. Приветствие  на  трех  языках: Здравствуйте, сәлеметсізбе, good morning.

Организационный  момент. Взаимное приветствие, фиксирование присутствующих, постановка цели занятия перед студентами, психологический настрой,  готовность студентов на работу в течение урока.

       Жоспар/ План/ Plan

Эпиграф :
Сегодня мы учимся вместе – Я, ваш учитель, и вы, мои ученики. Но в будущем ученик должен превзойти учителя, иначе в науке не будет прогресса
В.А.Сухомлинский

Актуализация знаний.
- дайте определение функции синус?

- как называется график синуса?

- дайте определение функции косинус?

- как называется график косинуса?

- дайте определение функции тангенс?

- как называется график тангенса?

- дайте определение функции котангенс?

- как называется график котангенса?

 

Повторим Табличные значения синусов, косинусов, тангенсов и котангенсов некоторых углов

 

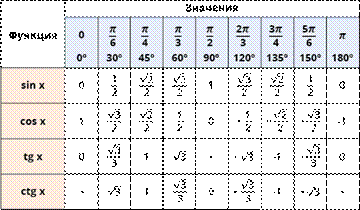
При каких значениях х верно равенство: 1)   

2)  

Введем понятие обратных тригонометрических функций.

 

Запишите новую тему.  «Обратные тригонометрические функции»

 

Изучение нового материала.

Какие тригонометрические функции знаете? Сколько их?

Сколько будет обратных тригонометрических функций?

 

Введем определение обратной функции:

Если функция у=f(x) монотонна на множестве Х, то она обратима.

Если функция у=f(x) определена и монотонно возрастает (убывает) на множестве X, областью значений является множество У, тогда существует обратная функция, причем эта функция определена и возрастает (убывает)  на У.

Эту функцию называют обратной по отношению к функции у=f(x)

Чтобы получить график функции, обратной по отношению к функции y=f(x), надо график функции y=f(x) преобразовать симметрично относительно прямой у=х.

 

Определим функцию, обратную y=sin x

Функция y=sin x определена, монотонно возрастает на отрезке [-π/2; π/2] и принимает все свои значения у ϵ[-1;1]. Следовательно, на отрезке  [-π/2; π/2] функция y=sin x имеет обратную функцию.

Обозначают y=arcsin x

Функция y=arcsin x определена на отрезке  [-1;1] и является монотонно возрастающей, множество значений функции [-π/2; π/2].

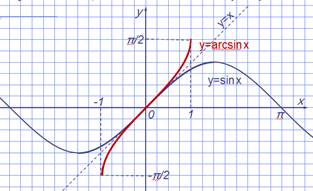
Используя график и свойства функции у = sinx, постараемся построить график функции

у = arcsinx и по графику перечислить свойства. Построим график у = sinx на отрезке [-π/2; π/2].

Построим прямую у = х. Отобразим построенный график относительно этой прямой.

 

Определение.

Если , то arcsin a – это такое число из отрезка  [-π/2; π/2], синус которого                 равен а. sin (arcsin a) = a arcsin(–a)= – arcsin a

Пример. 1. у=arcsin   означает sin y=  поэтому у= π/4

    2. arcsin()= – arcsin = – π/3   т.к  sin π/3 =

Определим функцию, обратную y=cos x

Функция y= cos x определена, монотонно убывает на отрезке [0; π] и принимает все свои значения в промежутке [-1;1]. Следовательно, на отрезке  [0; π] функция имеет обратную функцию.

Обозначают y=arccos x

Функция y=arccos x определена на отрезке  [-1;1] и является монотонно убывающей, множество значений функции [0; π].

 

 

 

 

 

 

 

 

 

Определение.

Если , то arccos a – это такое число из отрезка  [0; π], косинус которого                 равен а. cos (arccos a) = a arccos (–a)= π – arcсos a

 

Пример. 1. arccos1/2 = π/3

2. arccos(–1/2) = π – arccos1/2 = π – π/3 = 2π/3

 

 

Определим функцию, обратную y=tg x

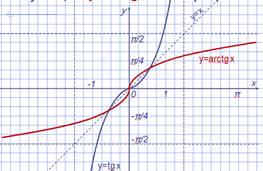Функция y= tg x определена, монотонно возрастает на интервале (-π/2; π/2) и принимает все свои значения (- ¥; +¥).

Следовательно, на интервале (-π/2; π/2)  функция y= tg x имеет обратную функцию.

Обозначают y=arctg x

Функция y=arctg x определена на R и является монотонно возрастающей, множество значений функции (-π/2; π/2) 

 

 

 

 

Определение.

arctg a – это такое число из отрезка  (-π/2; π/2), тангенс которого равен а. tg (arctg a) = a arctg (–a)= – arctg a

 

Пример. 1. arctg= π/3 

2. arctg (-1)= - arctg 1 = - π/4 

 

Определим функцию, обратную y=сtg x

Функция y= ctg x определена, монотонно убывает на отрезке [0; π] и принимает все свои значения на R.

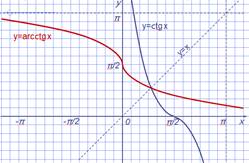Следовательно, имеет обратную функцию.

Обозначают y= arсctg x

Функция y=arcctg x определена на R и является монотонно убывающей, множество значений функции [0; π].

 

 

 

 

 

 

Определение.

arсctg a – это такое число из отрезка  (0; π), котангенс которого равен а. сtg (arсctg a) = a arсctg (–a)= π – arсctg a

 

Пример. 1. arсctg/3= π/3 

2. arсctg (-)=π - arсctg= π - π/6= 5π/6

 

Основные свойства тригонометрических функций:

arcsin(–х)= – arcsin х

arctg (–х)= – arctg х

arccos (–х)= π – arcсos х

arсctg (–х)= π – arcсtg х

arcsin х + arcos х = π/2

arctg х + arcсtg х = π/2

 

 

Закрепление изученного материала.

     № 70 (а,г,д,е)  71-72 (а,в)  74-75 (а,в)

 

                   

III.Бекіту/ Итог

Подведем итоги нашего занятия, и еще раз повторим то, что мы уже изучили.

какие тригонометрические  функции вы сегодня изучили?

IV.Үй  тапсырмасы/  Домашнее  задание

§ 6       № 70 (б,в)  71-72 (б,г)  74-75 (б,г)

 

Әдебиет/ Литература/Literature:

 

1.      Абылкасымова А.Е., Жумагулова З.А., Шойынбеков К.Д., Есенова М.И. Алгебра и начала анализа 10. – Алматы «Мектеп» 2014

2.      Синакевич С.В. Тригонометрические функции. – Москва, 1959

3.      Скачано с www.znanio.ru